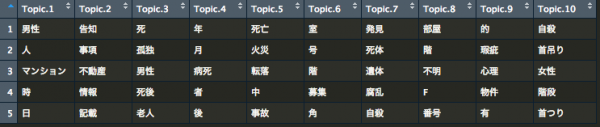
統計的仮説検定
検出力
一様最強力検定
ネイマン-ピアソンの基本定理
不偏検定
尤度比検定
尤度比検定(1標本のケース)
尤度比検定(2標本のケース)
\( \chi^2 \)適合度検定
分割表の検定
統計的仮説検定
確率ベクトル（標本確率変数）である\( X = (X_1, \dots, X_n) \)が標本空間\( \mathfrak X \)上にある分布\( P_{\theta} , \theta \in \Theta \)に従うとして、空集合ではない\( \Theta_0 \)は\( \Theta \)の真部分集合であらかじめ決まっているものとする。その前提のもとで、Xの従う分布が
帰無仮説
$$ P_{\theta} , \theta \in \Theta_0 $$
なのか、対立仮説
$$ P_{\theta} , \theta \in \Theta $$
なのかを主張する行為のことを統計的仮説検定と呼ぶ。なお、\( \Theta_0 \)が一つだけの場合は単純仮説、複数ある場合は複合仮説と呼ぶ。
仮説検定を行う際は、先ほどあげた標本空間\( \mathfrak X \)を、\( \mathfrak X = C \cup C^C \)との二つの領域に分割する。ここで、\( C \)は棄却域を\( C^C \)は受容域を表す。その際、以下のような棄却域の定義関数を考える。
$$
\varphi (X) =
\begin{cases}
1 \ (x \in C ) \\
0 \ (x \in C^C )
\end{cases} \\
0 \leq \varphi (x) \leq 1
$$
この定義関数\( \varphi (X) \)は検定関数と呼び、標本xを得たときに、確率\( \varphi (X) \)で帰無仮説（\( H_0 \)）を棄却する際に用いる。先ほどの定義関数の場合、0-1の値しかとらないので、非確率化検定と呼ばれる。他方、0-1でない場合は確率化検定と呼ばれる。
棄却域を決めると自ずと生じるものが、第一種の誤りと第二種の誤りです。
第一種の誤り
帰無仮説（\( H_0 \)）が正しいにも関わらず、それを棄却してしまうことによる誤り。
第二種の誤り
対立仮説（\( H_1 \)）が正しいにも関わらず、帰無仮説（\( H_0 \)）を受容したことによる誤り。
このどちらをも共に小さくすることはできません。
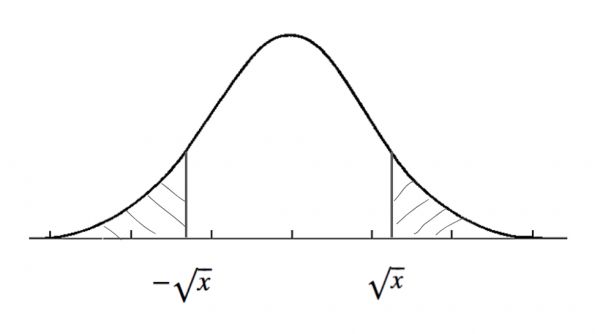
図にすることで理解が捗ります。
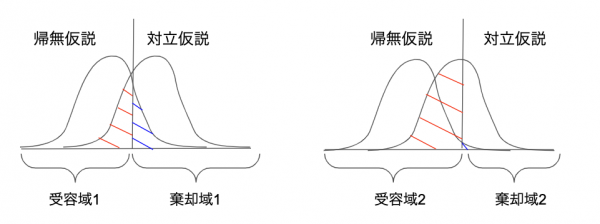
ここでは2種類の棄却域\( C_1, C2 \)を考えます。
図からわかるように、
$$ P(C_2 | H_0) < P(C_1 | H_0) \\
P(C_2^C | H_1) < P(C_1^C | H_1)
$$
となり、\( C_2 \)は第一種の誤りが小さい代わりに、第二種の誤りが大きくなっているのがわかります。
検出力
対立仮説\( H_1 \)が正しい時に、\( H_1 \)を受容する確率を検出力と呼ぶ。検定関数\( \varphi (X) \)の良さを表す。
$$\beta (\theta; \varphi ) = E_{\theta} \left [ \varphi (X) \right ] \ ( \theta \in \Theta_1 ) $$
以下の\( \alpha \)のことを検定関数\( \varphi (X) \)の大きさと呼ぶ。
$$ \alpha_0 = \sup_{\theta \in \Theta_0} E_{\theta}(\varphi(X))
$$
第一種の誤りをする確率に関しての、帰無仮説のもとに成り立つ\( \Theta_0 \)空間上での上限となる。
ここで\( \alpha \)を
$$0 \leq \alpha \leq 1$$
としたとき、
$$ \sup_{\theta \in \Theta_0} E_{\theta}(\varphi(X)) \leq \alpha
$$
となる検定を有意水準\( \alpha \)の検定と呼ぶ。
ようは、多くの人が有意差あるとかないとか言っているのは、この第一種の誤りをする確率のことで、社会科学では5%などに置くことが多い。
一様最強力検定
\( \alpha : 0 \leq \alpha \leq 1 \)が与えられたとき、水準\( \alpha \)の検定の中で検出力（\( H_1 \)が正しいときに、\( H_1 \)を受容できる確率）を一様に最大にするものが存在する場合、そのような検定を一様最強力検定（Uniformly Most Powerful test:UMP検定）と呼ぶ。
$$ E_{\theta} \left [ \varphi (X) \right ] \leq E_{\theta} \left [
\varphi_0 (X) \right ], \ \forall \theta \in \Theta_1 $$
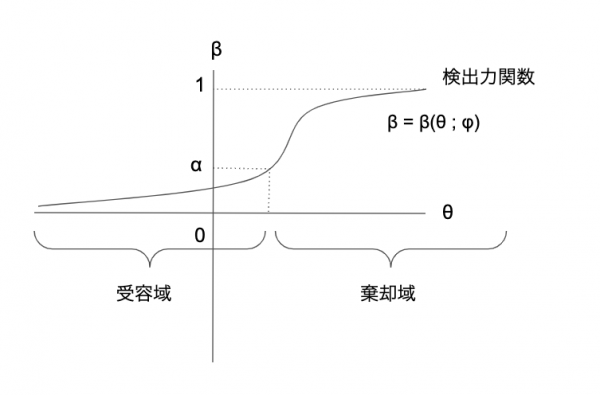
\( \theta \)の値が大きいときは、それが対立仮説に従うと採択する確率が高まり、帰無仮説の領域だと、値が小さいにも関わらず、対立仮説に従うと言ってしまっているので、検出力が下がる。
検出力関数の例
$$ \pi_{\gamma} (\theta) = P \left [ H_0 \ is \ rejected | X_1, \dots, X_n \sim f(x | \theta) \right ] \\
\pi_{\gamma} (\theta) \in [0, 1]
$$
という検出力関数について、Xの従う分布を以下のように仮定する。
$$ X_1, \dots, X_n \sim N(\theta, 25) $$
ここで、帰無仮説で
$$ H_0 : \theta \leq 17 $$
とする際の検出力について考える。
標本平均の\(\bar X\)が
$$ \bar X > 17 + 10 / \sqrt n $$
に従うとすると、検出力関数は、
$$ \pi_{\gamma} = P \left [ \bar X > 17 + 10/ \sqrt n | \theta \in \mathbb R \right ] \\
= P \left [ \frac{\sqrt n (\bar X – \theta)}{5} > \frac{17+ 10/ \sqrt n – \theta}{5 / \sqrt n} \right ] \\
= 1 – \Phi \left ( \frac{17+ 10/ \sqrt n – \theta}{5 / \sqrt n} \right ) $$
となる。
一応、可視化のためのコードも載せておきます。
|
|
import numpy as np import scipy import matplotlib.pyplot as plt import seaborn as sns n = 10 theta = np.linspace(-5, 30, 101) x = [(17+10/(n**(1/2)) - i)/(5/(n**(1/2))) for i in theta ] y = scipy.stats.norm.cdf(x) ax = sns.lineplot(x=theta, y=1-y) ax.set_xlabel('Theta') ax.set_ylabel('Power of detection') plt.show() |
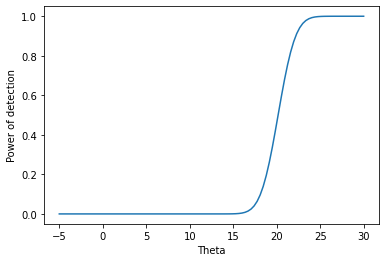
ネイマン-ピアソンの基本定理
確率分布\(P_{\theta}\)の確率密度関数\( f(x; \theta) \)について、以下の統計検定を行う際の最強力検定に関する定理をネイマン-ピアソンの基本定理と呼ぶ。
$$ H_0 : \theta = \theta_0 \\
H_1 : \theta = \theta_1 $$
ここでは有意水準を\( \alpha : 0 \leq \alpha \leq 1 \)とし、検定関数\( \varphi_0 (x) \)は以下の式で与えられる。
$$ \varphi_0 (x) = \begin{cases}
1 \ ( f(x ; \theta_1) > k f(x ; \theta_0) ) \\
\gamma \ ( f(x ; \theta_1) = k f(x ; \theta_0) ) \\
0 \ ( f(x ; \theta_1) < k f(x ; \theta_0) )
\end{cases}$$
ここで定数
$$ \gamma : 0 \leq \gamma \leq 1 \\
k : k \geq 0 $$
は以下の式から定まるものとする。
$$ E_{\theta_0} \left[ \varphi_0(X) \right ] = \alpha $$
ネイマン-ピアソンの基本定理の証明について
任意の統計検定の関数について、ネイマン-ピアソンの基本定理にしたがった統計検定の検出力を上回らないことを示せば良い。
Xが連続であるとして、
$$
C = \{ x \in \mathfrak X | f(x; \theta_1) > k f(x; \theta_0) \} \\
D = \{ x \in \mathfrak X | f(x; \theta_1) = k f(x; \theta_0) \} \\
E = \{ x \in \mathfrak X | f(x; \theta_1) < k f(x; \theta_0) \}
$$
とおくと、これらは互いに素であるから、
$$ \mathfrak X = C \cup D \cup E $$
と表される。
ここで統計検定の関数\( \varphi (X) \)を
$$
H_0 : \theta = \theta_0 \\
H_1 : \theta = \theta_1
$$
の検定問題に対する有意水準\( \alpha \)の任意の検定とする。
このとき、定義から\( \varphi (X) \)は
$$ E_{\theta_0} [ \varphi (X)] \leq \alpha $$
を満たす。
\( \varphi_0 (X) \)の定義から、
$$
E_{\theta_1}[ \varphi_0 (X) ] – E_{\theta_1}[ \varphi (X) ] \\
= \int_{\mathfrak X} \varphi_0 (X) f(x ; \theta_1) dx – \int_{\mathfrak X} \varphi (X) f(x ; \theta_1) dx \\
= \int_{\mathfrak X} (\varphi_0 (X) – \varphi (X) ) f(x ; \theta_1) dx \\
= \int_{C} (1 – \varphi (X) ) f(x ; \theta_1) dx + \int_{D} (\gamma – \varphi (X) ) f(x ; \theta_1) dx + \int_{E} ( – \varphi (X) ) f(x ; \theta_1) dx \\
\geq \int_{C} (1 – \varphi (X) ) (k f(x;\theta_0))dx + \int_{D} (\gamma – \varphi (X) ) (k f(x;\theta_0))dx + \int_{E} ( – \varphi (X) ) (k f(x;\theta_0))dx \\
= k \int_{C} (1 – \varphi (X) )f(x;\theta_0)dx + k \int_{D} (\gamma – \varphi (X) )f(x;\theta_0)dx + k \int_{E} ( – \varphi (X) )f(x;\theta_0)dx \\
= k \int_{\mathfrak X} (\varphi_0 (X) – \varphi (X) ) f(x ; \theta_1) dx \\
= k \{E_{\theta_0}[ \varphi_0 (X) ] – E_{\theta_0}[ \varphi (X) ]\} \\
= k \{ \alpha – E_{\theta_0}(\varphi(X))\} \\
\geq 0$$
よって、
$$ E_{\theta_1}[ \varphi_0 (X) ] \geq E_{\theta_1}[ \varphi (X) ] $$
となり、\( \varphi_0 (X) \)が任意のものよりも大きな検出力を持つことから、有意水準\( \alpha \)の最強力検定であることが示された。
ネイマン-ピアソンによる最強力検定の例（正規分布）
平均が未知で分散が既知のケースにおいて、確率変数が\( X_1, \dots , X_n \sim N(\mu, \sigma_0^2) \)に従うとして、以下の検定問題を考え、有意水準\( \alpha \)の最強力検定を求める。
$$
H_0 : \mu = \mu_0 \\
H_1 : \mu < \mu_0
$$
これは単純仮説と単純対立仮説からなる検定問題なので、以下のように書き換えることができる。
$$
H_0 : \mu = \mu_0 \\
H_1 : \mu = \mu_1 \\
(\mu_1 < \mu_0)
$$
なお、この例は片側検定問題となる。
\( X_i \)の確率密度関数を\( f(x_i ; \mu) \)として、ネイマン-ピアソンの基本定理に従うと、有意水準\( \alpha \)の最強力検定は以下のようになる。
$$ \varphi_0 (x) = \begin{cases}
1 \ ( \prod_{i=1}^n f(x_i ; \mu_1) > k \prod_{i=1}^n f(x_i ; \mu_0) ) \\
\gamma \ ( \prod_{i=1}^n f(x_i ; \mu_1) = k \prod_{i=1}^n f(x_i ; \mu_0)) \\
0 \ ( \prod_{i=1}^n f(x_i ; \mu_1) < k \prod_{i=1}^n f(x_i ; \mu_0) )
\end{cases}$$
ここで、
$$
\gamma \in [0, 1] \\
k \in [0, \infty ]
$$
は
$$ E_{\mu_0} [ \varphi_0(X) ] = \alpha $$
を満たす定数で与えられるものとする。
\( X = (X_1, \dots , X_n ) \)が連続型の場合、
$$P_{\mu_j} \left \{ \prod_{i=1}^n f(x_i ; \mu_1) = k \prod_{i=1}^n f(x_i ; \mu_0) \right \} = 0 \\
j = 0, 1$$
であるから、このケースは無視することができる。
仮定より、
$$ \prod_{i=1}^n f(x_i ; \mu) = \prod_{i=1}^n \frac{1}{\sqrt {2\pi} \sigma_0} e^{-\frac{(x_i – \mu)^2}{2\sigma_0^2}} \\
= \frac{1}{(\sqrt {2\pi})^n \sigma_0^n} e^{-\frac{\sum_{i=1}^n (x_i – \mu)^2 }{2\sigma_0^2}} \\
= \frac{1}{(\sqrt {2\pi}\sigma_0)^n } e^{-\frac{n(\bar x – \mu)^2 + \sum_{i=1}^n(x_i – \bar x)^2}{2\sigma_0^2}}
$$
よって検定関数において、棄却するケースについて以下のように書き表すことができる。
$$\prod_{i=1}^n f(x_i ; \mu_1) > k \prod_{i=1}^n f(x_i ; \mu_0) \\
\Leftrightarrow \frac{\prod_{i=1}^n f(x_i ; \mu_1)}{\prod_{i=1}^n f(x_i ; \mu_0)} > k \\
\Leftrightarrow \frac{\frac{1}{(\sqrt {2\pi}\sigma_0)^n } e^{-\frac{n(\bar x – \mu_1)^2 + \sum_{i=1}^n(x_i – \bar x)^2}{2\sigma_0^2}}}{\frac{1}{(\sqrt {2\pi}\sigma_0)^n } e^{-\frac{n(\bar x – \mu_0)^2 + \sum_{i=1}^n(x_i – \bar x)^2}{2\sigma_0^2}}} \\
\Leftrightarrow e^{\frac{n}{2\sigma_0^2} ((\bar x – \mu_0)^2 – (\bar x – \mu_1)^2) } > k \\
\Leftrightarrow (\bar x – \mu_0)^2 – (\bar x – \mu_1)^2 > \frac{2\sigma_0^2}{n} \log k = k’
$$
ここで、\( \mu_1 < \mu_0 \)より
$$(\bar x – \mu_0)^2 – (\bar x – \mu_1)^2 < 0$$
であるから、
$$ \bar x < \frac{\mu_1^2 – \mu_0^2}{2(\mu_1 – \mu_0)} = k” $$
となる。
一方、\( H_0 \)が真のとき、\( \bar X \)は\( N \left ( \mu_0, \frac{\sigma_0^2}{n} \right ) \)に従うので、
$$\alpha = E_{\mu_0}[ \varphi_0 (X) ] \\
= P_{\mu_0} \left \{ \prod_{i=1}^n f(x_i ; \mu_1) > k \prod_{i=1}^n f(x_i ; \mu_0) \right \} \\
= P_{\mu_0} \left \{ \bar X < k” \right \} \\
= \int_{-\infty}^{k”}\frac{\sqrt{n}}{\sqrt{2\pi}\sigma_0}e^{-\frac{n(t-\mu_0)^2}{2\sigma_0^2}}dt
$$
ここで\( \frac{\sqrt{n}(t-\mu_0)}{\sigma_0} = u \)、\( k_0 = \frac{\sqrt{n}(k” – \mu_0)}{\sigma_0} \)とおいて変数変換を行うと、
$$ \alpha = \int_{-\infty}^{k_0} \frac{1}{\sqrt{2\pi}}e^{-\frac{u^2}{2}}du \\
= \Phi (k_0)
$$
となる。\(\Phi(\cdot)\)は\( N(0,1) \)の分布関数を表すので、標準正規分布表から\( \Phi (k_0) = \alpha \)をみたす\( k_0 \)の値を読み取ることで、以下のような今回の統計検定の棄却域が得られる。
$$k^{*} = \mu_0 + \frac{\sigma_0}{\sqrt{n}}k_0 = \mu_0 – \frac{\sigma_0}{\sqrt{n}}z(\alpha) $$
なお、これは\( \mu_1 \)の水準に無関係に決まる。
ネイマン-ピアソンによる最強力検定の例（ベルヌーイ分布）
確率pが未知で確率変数mが既知のケースにおいて、確率変数が\( X_1, \dots , X_n \sim B_N(m, p) \)として、以下の検定問題を考え、有意水準\( \alpha \)の最強力検定を求める。
$$
H_0 : p = p_0 \\
H_1 : p < p_0
$$
これは単純仮説と単純対立仮説からなる検定問題なので、以下のように書き換えることができる。
$$
H_0 : p = p_0 \\
H_1 : p = p_1 \\
( p_1 < p_0)
$$
仮定より、\( X = ( X_1, \dots , X_n ) \)の確率関数は
$$\prod_{i=1}^n f(x_i ; p) = \prod_{i=1}^n {}_m C _{x_i}p^{x_i}(1-p)^{m-x_i} \\
= p^{\sum_{i=1}^n x_i}(1-p)^{mn – \sum_{i=1}^n x_i} \prod_{i=1}^n {}_m C _{x_i} $$
となる。
対立仮説が正しいのであれば、尤度の比において以下の関係となる。
$$\frac{\prod_{i=1}^n f(x_i ; p_1)}{ \prod_{i=1}^n f(x_i ; p_0) } > k \\
\Leftrightarrow \frac{ p_1^{\sum_{i=1}^n x_i}(1-p_1)^{mn – \sum_{i=1}^n x_i} \prod_{i=1}^n {}_m C _{x_i}}{p_0^{\sum_{i=1}^n x_i}(1-p_0)^{mn – \sum_{i=1}^n x_i} \prod_{i=1}^n {}_m C _{x_i}} > k \\
\Leftrightarrow \left ( \frac{p_1(1-p_0)}{p_0(1-p_1)} \right )^{\sum_{i=1}^nx_i} \times \left ( \frac{1-p_1}{1-p_0} \right )^{mn} > k \\
\Leftrightarrow \left ( \frac{p_1(1-p_0)}{p_0(1-p_1)} \right ) ^{ \sum_{i=1}^n x_i } > k’ = \left ( \frac{1-p_0}{1-p_1} \right )^{mn}k $$
\( p_1 < p_0 \)であることから、
$$\left ( \frac{p_1(1-p_0)}{p_0(1-p_1)} \right ) < 1$$
となり、1よりも小さな項の指数なので、これを満たす\( \sum_{i=1}^n x_i \)であるために、
$$\Leftrightarrow \sum_{i=1}^n x_i < k”$$
が満たされる必要がある。
よってこの検定問題における有意水準\( \alpha \)の最強力検定はネイマン-ピアソンの基本定理に従うと、
$$ \varphi_0 (x) = \begin{cases}
1 \ ( \sum_{i=1}^n < k” ) \\
\gamma \ ( \sum_{i=1}^n = k” ) \\
0 \ ( \sum_{i=1}^n > k” )
\end{cases}
$$
によってなされる。
なお、
$$ \gamma \in [0, 1] \\
k” \in [0, \infty ] $$
は
$$E_{p_0}[ \varphi_0 (X) ] = \alpha $$
を満たす定数によって与えられる。
帰無仮説\( H_0 \)が真のとき\( \sum_{i=1}^n X_i \)は\( B_N(mn, p_0) \)に従うので、\( \gamma, k” \)は以下の式を解くことで求められる。
$$ E_{p_0} [ \varphi_0 (x)] = 1 \times P_{p_0} \left \{ \sum_{i=1}^n x_i < k” \right \} \\
+ \gamma \times P_{p_0} \left \{ \sum_{i=1}^n x_i = k” \right \} \\
+ 0 \times P_{p_0} \left \{ \sum_{i=1}^n x_i > k” \right \} \\
= \sum_{j < k”} {}_{mn} C _j p_0^j (1-p_0)^{mn-j} + \gamma {}_{mn} C _{k”} p_0^{k”} (1- p_0)^{mn – k”} \\
= \alpha $$
\( B_N(mn, p_0) \)の分布関数を\( F(x ; p_0) \)としたとき、
$$F(k-1; p_0) \leq \alpha $$
を満たす最大の整数kを\( k” \)として、
$$ \gamma = \frac{\alpha – F(k” – 1 ; p_0 )}{F(k”;p_0) – F(k” – 1 ; p_0)} $$
ただし、\( F(0 ; p_0) \leq \alpha \)とする。\( F(0 ; p_0) \geq \alpha \)の場合は、
$$k” = 0 \\
\gamma = \frac{\alpha}{F(0; p_0)}$$
となる。これらは対立仮説の\(p_1\)に関係なく決まるため、一様最強力検定となる。
不偏検定
単純仮説ではなく複合仮説の場合、先ほどのような検定を不偏検定と呼ぶ。
検定問題は以下のようになる。
$$ H_0 : \theta \in \Theta_0 \\
H_1 : \theta \in \Theta_1 \ ( = \Theta – \Theta_0 ) $$
この検定問題で水準\( \alpha \)の検定\( \varphi (X) \)でその検出力が\( \alpha \)以上、
$$ \beta (\theta ; \varphi ) := E_{\theta} [ \varphi (X)] \geq \alpha, \forall \theta \in \Theta_1 $$
を満たす検定\( \varphi (X) \)を水準\( \alpha \)の不偏検定と呼び、水準\( \alpha \)の不偏検定の中で検出力を一様に最大にするものを水準\( \alpha \)の一様最強力不偏検定と呼ぶ。
不偏検定の際の検出力関数は以下の図のようになる。検出力関数がわかれば、\( \alpha \)（第一種の誤りをする確率）を与えたもとで棄却域が決まる。
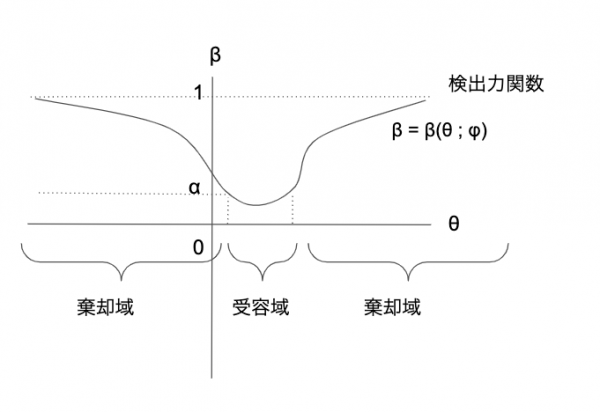
不偏検定に関する定理
まず前提として、\( \theta \)を母数として、\( X = (X_1, \dots , X_n) \)の確率関数\( f(x, \theta) \)が以下の表現で表されるとする。
$$ f(x, \theta) = C(\theta)e^{\theta T(x)}h(x) $$
\( \theta_0, \theta_1, \theta_2 (\theta_1 < \theta_2) \)を与えられたものとして、以下の複合仮説の仮説検定問題を考える。
(1)
$$ H_0 : \theta_1 \leq \theta \leq \theta_2 \\
H_1 : \theta < \theta_1 \ or \ \theta > \theta_2
$$
(2)
$$ H_0 : \theta = \theta_0 \\
H_1 : \theta \neq \theta_0
$$
このような仮説検定問題を両側検定問題と呼ぶ。
検定問題(1),(2)に対する一様最強力不偏検定\( \varphi_0(X) \)は以下の式で与えられる。
$$
\varphi_0 (X) =
\begin{cases}
1 \ ( T(x) < k_1 \ or \ T(x) > k_2 ) \\
\gamma \ ( T(x) = k_i , i=1, 2 ) \\
0 \ (k_1 < T(x) < k_2)
\end{cases} \\
0 \leq \varphi (x) \leq 1
$$
ここで、定数\( \gamma_i \in [0,1], k_i \geq 0, (i = 1, 2) \)は検定問題(1)については以下の式により定まる。
$$E_{\theta_1}[ \varphi_0 (X) ] = E_{\theta_2} [\varphi_0 (X)] = \alpha $$
一方、検定問題(2)については以下の式により定まる。
$$ E_{\theta_0}[\varphi_0 (X)] = \alpha \\
E_{\theta_0}[T(X) \varphi_0 (X)] =E_{\theta_0}[T(X)] \alpha
$$
以前のネイマン-ピアソンの基本定理は確率の積和（尤度）があったが、この定理ではより一般的な記述がされており、帰無仮説や対立仮説のパラメータも記されていない。しかしながら、非常に似ている。
不偏検定の例（正規分布（平均が未知、分散が既知のケース））
確率変数が以下に従うと仮定する。
$$X_1, X_2, \dots , X_n \sim N(\mu, \sigma_0^2)$$
ここで以下の検定問題を考える。
$$ H_0 : \mu = \mu_0 \\
H_1 : \mu \neq \mu_0 $$
この検定問題に対する、一様最強力不偏検定を行う。
仮定より、\( X = (X_1,\dots , X_n) \)の確率密度関数の積は
$$ \prod_{i=1}^n f(x_i ; \mu) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi}\sigma_0}e^{-\frac{(x_i – \mu)^2}{2\sigma_0^2}} \\
= \frac{1}{(\sqrt{2\pi}\sigma_0)^n}e^{-\frac{(x_i – \mu)^2}{2\sigma_0^2}} \\
= \frac{1}{(\sqrt{2\pi}\sigma_0)^n} e^{-\frac{n\mu^2}{2\sigma_0^2}}e^{\mu \frac{\sum_{i=1}^n x_i}{\sigma_0^2}}e^{- \frac{\sum_{i=1}^n x_i^2}{2\sigma_0^2}} $$
ここで、統計量として以下を定義する。
$$ T(x) = \frac{1}{\sigma_0^2} \sum_{i=1}^n x_i $$
これを用いると先ほどの尤度は以下のような指数型分布になる。
$$ \prod_{i=1}^n f(x_i ; \mu) = C(\mu) e^{\mu T(x)}h(x) $$
不偏検定に関する定理を用いることで、水準\( \alpha \)の一様最強力不偏検定の棄却域は以下で与えられる。
$$ C = \left \{ x = (x_1, \dots, x_n) \in \mathbb R^n | \frac{1}{\sigma_0^2} \sum_{i=1}^n x_i < nk_1 \ or \ \frac{1}{\sigma_0^2} \sum_{i=1}^n x_i > nk_2 \right \} $$
ここで、\(k_1, k_2\)は、
$$ P_{\mu_0} \{ C \} = \alpha $$
および、
$$ E_{\mu_0} \left \{ \frac{1}{\sigma_0^2} \sum_{i=1}^n x_i \cdot 1_c(x) \right \} = E_{\mu_0} \left \{ \frac{1}{\sigma_0^2} \sum_{i=1}^n x_i \right \} \cdot \alpha $$
を満たす定数となる。(\( 1_c(x) \)はインデックス関数。)
各\( X_i \)が独立に\( N(\mu, \sigma_0^2) \)に従い、\( \bar X = \frac{1}{n} \sum_{i=1}^n \)が\( N(\mu, \frac{\sigma_0^2}{n}) \)に従う。
ここで水準\( \alpha \)を以下のように書くことができる。
$$ \alpha = P_{\mu_0} \left \{ \bar X < k_1 \sigma_0^2 \ or \ \bar X > k_2 \sigma_0^2 \right \} $$
ここで、
$$ k’_i = \frac{\sqrt {n} (k_i \sigma_0^2) – \mu_0}{\sigma_0}, i =1, 2 $$
とおくと、
$$ \alpha = P_{\mu_0} \left \{ \frac{\bar X – \mu_0}{ \sqrt{\frac{\sigma_0^2}{n}}} < k’_1 \right \} + P_{\mu_0} \left \{ \frac{\bar X – \mu_0}{ \sqrt{\frac{\sigma_0^2}{n}}} > k’_2 \right \} \\
= \Phi (k’_1) + 1 – \Phi (k’_2) $$
となる。
他方、不偏検定に関する定理より、
$$ E_{\mu_0} \left \{ \bar X \cdot 1_C(X) \right \} = E_{\mu_0} \left \{ \bar X \right \}\alpha $$
ここで、
$$ z = \frac{\sqrt{n}(\bar X – \mu_0)}{\sigma_0} $$
とおくと、\( \bar X = \mu_0 + \frac{\sigma_0}{\sqrt{n}}Z \)なので、
$$ E_{\mu_0} \left \{ \bar X \cdot 1_C(X) \right \} = E_{\mu_0} \left \{ ( \mu_0 + \frac{\sigma_0}{\sqrt{n}}Z ) \cdot 1_C(X) \right \} \\
= \mu_0 E_{\mu_0} \left \{ 1_C(X) \right \} + \frac{\sigma_0}{\sqrt{n}} E_{\mu_0} \left \{z \cdot 1_C(X) \right \} \\
= \alpha \mu_0 + \frac{\sigma_0}{\sqrt{n}} E_{\mu_0} \left \{z \cdot 1_C(X) \right \}$$
よって、
$$ E_{\mu_0} \left \{ z \cdot 1_C(X) \right \} = 0 $$
となる。
\( C = \left \{ z < k’_1 \ or \ z > k’_2 \right \} \)と書けることから、これを書き換えると、
$$ \int_{-\infty}^{k’_1}z \phi (z) dz + \int_{k’_2}^{+\infty}z \phi (z) dz = 0 $$
となる。
すなわち、
$$ \frac{1}{ \sqrt{2 \pi}} e^{ – \frac{(k’_1)^2}{2}} = \frac{1}{\sqrt{2 \pi}} e^{ – \frac{(k’_2)^2}{2} } $$
となる。これより、
$$ | k’_1 | = | k’_2 | $$
から、
$$ k’_1 = -k’_2 < 0 $$
となる。
以上から、水準\( \alpha \)の一様最強力不偏検定の棄却域は
$$ \bar X < k_1\sigma_0^2 \\
\bar X > k_2 \sigma_0^2 $$
で与えられる。
ここで、
$$ k_1 = \left ( \mu_0 + \frac{\sigma_0}{\sqrt{n}}k’_1 \right ) / \sigma_0^2 \\
k_2 = \left ( \mu_0 – \frac{\sigma_0}{\sqrt{n}}k’_1 \right ) / \sigma_0^2 $$
となり、\( k’_1 \)は
$$ \Phi ( k’_1 ) = \frac{\alpha}{2} $$
を満たす、標準正規分布の値、\( k’_1 = -z \left ( \frac{\alpha}{2} \right ) \)となる。
不偏検定の例（正規分布（平均が既知、分散が未知のケース））
確率変数が以下に従うと仮定する。
$$X_1, X_2, \dots , X_n \sim N(\mu_0, \sigma^2)$$
ここで以下の検定問題を考える。
$$ H_0 : \sigma^2 = \sigma_0^2 \\
H_1 : \sigma^2 \neq \sigma_0^2 $$
この検定問題に対する、一様最強力不偏検定を行う。
仮定より、\( X = (X_1,\dots , X_n) \)の確率密度関数の積は
$$ \prod_{i=1}^n f(x_i ; \sigma^2) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x_i – \mu_0)^2}{2\sigma^2}} \\
= \frac{1}{(\sqrt{2\pi}\sigma)^n}e^{-\frac{(x_i – \mu_0)^2}{2\sigma^2}} $$
ここで、統計量として以下を定義する。
$$ T(x) = \frac{ \sum_{i=1}^n (x_i – \mu_0)^2 }{\sigma_0^2}$$
さらに、
$$ \theta = – \frac{\sigma_0^2}{2\sigma_2} $$
と考えると、先ほどの尤度は以下のような指数型分布になる。
$$ \prod_{i=1}^n f(x_i ; \sigma^2) = C(\theta) e^{\theta T(x)}h(x) $$
不偏検定に関する定理を用いることで、水準\( \alpha \)の一様最強力不偏検定の棄却域は以下で与えられる。
$$ C = \left \{ x = (x_1, \dots, x_n) \in \mathbb R^n | T(x) < k_1 \ or \ T(x) > k_2 \right \} $$
ここで、\(k_1, k_2\)は、
$$ P_{\sigma_0^2} \{ C \} = \alpha $$
および、
$$ E_{\sigma_0^2} \left \{ T(x) \cdot 1_c(x) \right \} = E_{\sigma_0^2} \left \{ T(x) \right \} \cdot \alpha $$
を満たす定数となる。(\( 1_c(x) \)はインデックス関数。)
\(H_0\)が真のとき、\( T(x)= \frac{\sum_{i=1}^n (x_i – \mu_0)^2 }{\sigma_0^2} \)は自由度nの\( \chi ^2 \)分布に従うので、
$$ P_{\sigma_0^2} \{ C \} = P_{\sigma_0^2} \{ T(x) < k_1 \ or \ T(x) > k_2 \} \\
= \int_0^{k_1}g_n (x) dx + \int_{k_2}^{\infty}g_n (x) dx = \alpha $$
となる。
$$ E_{\sigma_0^2} \{ T(x) \cdot 1_c(x) \} = \int_{0}^{k_1}x g_n(x)dx + \int_{k_2}^{\infty}x g_n(x)dx $$
ここで、
$$ \int_{a}^{b}xg_n(x)dx = \int_{a}^{b} \frac{1}{\Gamma \left (
\frac{n}{2} \right )2^{\frac{n}{2}} }x^{\frac{n}{2}}e^{-\frac{x}{2}} \\
= \frac{\Gamma \left ( \frac{n+2}{2} \right ) 2^{\frac{n+2}{2}} }{\Gamma \left ( \frac{n}{2} \right ) 2^{\frac{n}{2}}} \int_{a}^{b}\frac{1}{\Gamma \left ( \frac{n+2}{2} \right ) 2^{\frac{n+2}{2}}} x^{\frac{n+2}{2}-1}e^{-\frac{x}{2}}dx \\
= n \int_{a}^{b} g_{n+2}(x)dx $$
とすると、先ほどの式は、
$$ E_{\sigma_0^2} \{ T(x) \cdot 1_c(x) \} = n \int_{0}^{k_1}g_{n+2}(x)dx + n \int_{k_2}^{\infty}g_{n+2}(x)dx \\
= n \alpha$$
となる。以上より、一様最強力不偏検定の棄却域\( k_1, k_2 \)は、
$$\int_{0}^{k_1}g_n(x)dx + \int_{k_2}^{\infty}g_n(x)dx = \alpha \\
\int_{0}^{k_1}g_{n+2}(x)dx + \int_{k_2}^{\infty}g_{n+2}(x)dx = \alpha$$
を同時に満たすような\( k_1, k_2 \)を選べば良い。
実際には簡単にするために、
$$ \int_{0}^{k_1}g_{n}(x) dx = \int_{k_2}^{\infty}g_{n}(x) dx = \frac{\alpha}{2} $$
となるような\( k_1, k_2 \)を\( \chi^2 \)分布表から読み取って、
$$ k_1 = \chi^2 \left ( 1 – \frac{\alpha}{2}; n \right ) \\
k_2 = \chi^2 \left ( \frac{\alpha}{2}; n \right ) $$
によって近似的に水準\( \alpha \)の一様最強力不偏検定の棄却域として、
$$ \frac{\sum_{i=1}^n (x_i – \mu_0)^2 }{\sigma_0^2} < k_1 \\
\frac{\sum_{i=1}^n (x_i – \mu_0)^2 }{\sigma_0^2} > k_2 $$
が採用される。
尤度比検定
仮説検定論における普遍的な検定方式のこと。帰無仮説に従う際の尤度と、真のパラメータに従う際の尤度の比をもとに検定を行う。
確率ベクトル(\( X = (X_1, \dots , X_n) \))が確率密度関数(\( f(X_1, \dots , X_n; \theta) \))に従うとして、
真のパラメータ(\( \theta \in \Theta \))、
帰無仮説に従うパラメータ(\( \theta_0 \ ( \neq \phi ) \ \in \Theta \))、
対立仮説に従うパラメータ(\( \theta_1 = \Theta – \Theta_0 \ ( \neq \phi ) \))
に対して、以下の仮説検定問題を考える。
$$ H_0 : \theta \in \Theta_0 \\
H_1 : \theta \in \Theta_1 $$
ここで、固定された各標本(\( x = (x_1, \dots , x_n) \))に対して、尤度の比を求める。
$$ \lambda (x) := \frac{ \sup_{\theta \in \Theta_0} f(x_1, \dots ,x_n ; \theta) }{ \sup_{\theta \in \Theta} f(x_1, \dots ,x_n ; \theta) } $$
適当に定められた定数cに対して、
$$ \lambda (x) < c $$
となるとき、仮説\( H_0 \)を棄却し、そうでないとき\( H_0 \)を受容するという検定方式を考える。ここでcは
$$ \sup_{\theta \in \Theta_0} P_{\theta} \left \{ \lambda (X) < c \right \} = \alpha $$
を満たすものとする。このような検定方式を水準\( \alpha \)の尤度比検定と呼び、\( \lambda (x) \)を尤度比統計量と呼ぶ。
尤度比検定は複合仮説からなる検定問題において、\( \Theta_0, \Theta_1 \)をそれぞれ1つの母数で代表させることで、複合仮説検定問題を単純仮説と単純対立仮説からなる検定問題に置き換えることができる。
他にも尤度比検定は、データが十分に大きい際に、検出力が1に収束するという一致性や、漸近的に最大の検出力を持つという漸近有効性などの性質も持ち合わせている。
尤度比検定に関する定理
\( n \to + \infty \)とすると、統計量\( -2 log \lambda (x) \)は仮説\( H_0 \)のもとで自由度qの\( \chi^2 \)分布に収束する。ここでは\( g(t) \)がその確率密度関数となる。
$$ \theta \in \Theta_0 \\
\lim_{n \to \infty} P_{\theta} \left \{ -2 \log \lambda (x) \leq z \right \} \\
= \int_{0}^{z}g(t)dt \\
\forall z \in (0, \infty) $$
尤度比検定(1標本のケース)
ここではデータが1つの標本から独立にそれぞれ\( N(\mu, \sigma^2) \)に従うケースを想定する。
その上で、
「\(\mu\)が未知で\(\sigma^2 = \sigma_0^2 \)が既知の場合」
「\(\mu, \sigma^2\)ともに未知の場合」についての尤度比検定を行う。
\(\mu\)が未知で\(\sigma^2 = \sigma_0^2 \)が既知の場合
ここでは以下の検定問題を扱う。
$$ H_0 : \mu = \mu_0 \\
H_1 : \mu \neq \mu_0 $$
仮定から、確率ベクトル（標本確率変数）である\( X = (X_1, \dots, X_n) \)の確率密度関数は
$$ f(x_1, \dots, x_n ; \theta) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi}\sigma_0} e^{- \frac{(x_i – \mu)^2}{2\sigma_0^2}} \\
= \left ( \frac{1}{\sqrt{2\pi} \sigma_0} \right )^n e^{ – \frac{\sum_{i=1}^n(x_i – \bar x)^2 + n(\bar x – \mu)^2 }{2\sigma_0^2} } $$
\(\mu\)の\( \Theta = \mathbb R^1 \)における最尤解は\( \hat \mu = \bar X \)となるので、尤度比は帰無仮説に従う確率密度関数と真のパラメータの従う確率密度関数であるから、
$$ \lambda (x) = \frac{f(x_1, \dots, x_n ; \mu_0)}{f(x_1, \dots, x_n ; \hat \mu)} \\
= \frac{ \left ( \frac{1}{\sqrt{2\pi} \sigma_0} \right )^n e^{ – \frac{ \sum_{i=1}^n(x_i – \bar x)^2 + n(\bar x – \mu_0)^2 }{2\sigma_0^2} }}{ \left ( \frac{1}{\sqrt{2\pi} \sigma_0} \right )^n e^{ – \frac{\sum_{i=1}^n(x_i – \bar x)^2 + n(\bar x – \bar x)^2 }{2\sigma_0^2} }} \\
= e^{- \frac{n(\bar x – \mu_0)^2}{2\sigma_0^2}} $$
ここで、水準\(\alpha\)の尤度比検定の棄却域は最後の式の指数部分の
$$ | \bar x – \mu_0 | > c$$
で与えられる。
定数cは
$$ P_{\mu_0} \{ | \bar X – \mu_0 | > c \} = \alpha $$
より定まる。
帰無仮説\( H_0 \)のもとで\(\bar X\)は\( N \left ( \mu_0 , \frac{\sigma_0^2}{n} \right ) \)に従うので、
$$ \alpha = P_{\mu_0} { \frac{ \sqrt{n} | \bar X – \mu_0 |}{\sigma_0} > \frac{\sqrt{n}c}{\sigma_0} } \\
= \int_{k}^{\infty} \phi (t)dt + \int_{-\infty}^{-k} \phi (t) dt \\
= 2 \left ( 1 – \Phi (k) \right ) $$
したがって、標準正規分布から水準\(\alpha\)を満たすようなkの値を見つければよい。
\(\mu, \sigma^2\)ともに未知の場合
ここでは以下の二つの検定問題を扱う。
「平均に関する検定」
「分散に関する検定」
平均に関する検定
$$ H_0 : \mu = \mu_0 \\
H_1 : \mu \neq \mu_0 $$
真のパラメータは以下で表される。
$$ \theta = \left \{ (\mu, \sigma^2) | \mu \in \mathbb R^1 , \sigma^2 > 0 \right \} $$
同様に帰無仮説に従う場合のパラメータは、
$$ \theta_0 = \left \{ (\mu_0, \sigma^2) | \sigma^2 > 0 \right \} $$
対立仮説に従う場合のパラメータは、
$$ \theta_1 = \left \{ (\mu, \sigma^2) | \mu (\neq \mu_0) \in \mathbb R^1 , \sigma^2 > 0 \right \} $$
で表される。
仮定から、確率ベクトル（標本確率変数）である\( X = (X_1, \dots, X_n) \)の確率密度関数は
$$ f(x_1, \dots, x_n ; \mu, \sigma^2) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi}\sigma} e^{- \frac{(x_i – \mu)^2}{2\sigma^2}} \\
= \left ( \frac{1}{\sqrt{2\pi}} \right )^n \left ( \frac{1}{\sigma^2} \right )^{\frac{n}{2}} e^{ – \frac{\sum_{i=1}^n(x_i – \bar x)^2 + n(\bar x – \mu)^2 }{2\sigma^2} } $$
ここで、\( \theta = (\mu, \sigma^2) \)が\( \Theta_0\)上を動くときに、\( \mu = \mu_0\)なので、尤度を最大にする問題において以下のように書くことができる。
$$ \sup_{\theta \in \Theta_0} f(x_1, \dots, x_n ; \mu, \sigma^2) = \sup_{\sigma^2 > 0} f(x_1, \dots, x_n ; \mu_0, \sigma^2) \\
= \left ( \frac{1}{\sqrt{2\pi}} \right )^n \left ( \frac{1}{ \hat \sigma^2} \right )^{\frac{n}{2}} e^{ – \frac{\sum_{i=1}^n(x_i – \mu_0)^2}{2 \hat \sigma^2} } $$
ここで\( \hat \sigma^2 = \frac{1}{n} \sum_{i=1}^n (x_i – \mu_0)^2 \)とすると、
$$ = \left ( \frac{1}{\sqrt{2\pi}} \right )^n \left ( \frac{1}{ \hat \sigma^2} \right )^{\frac{n}{2}} e^{-\frac{n}{2}} $$
一方、\( \theta = (\mu, \sigma^2) \)が真のパラメータ\( \Theta\)上を動くときに、最尤解\( (\hat \mu, \hat \sigma^2)\)が、以下で与えられる。
$$ \hat \mu = \bar x \ \left ( \frac{1}{n} \sum_{i=1}^n \bar x \right ) \\
\hat \sigma = \frac{1}{n}\sum_{i=1}^n (x_i – \bar x)^2 $$
よって尤度を最大にする問題において以下のように書くことができる。
$$ \sup_{\theta \in \Theta} f(x_1, \dots, x_n ; \mu, \sigma^2) = f(x_1, \dots, x_n ; \hat \mu,\hat{\hat{\sigma^2}}) \\
= \left ( \frac{1}{\sqrt{2\pi}} \right )^n \left ( \frac{1}{ \hat{\hat{\sigma^2}}} \right )^{\frac{n}{2}} e^{ – \frac{\sum_{i=1}^n(x_i – \hat \mu)^2}{2 \hat{\hat{\sigma^2}}} } $$
ここで、先ほどと同じように\( \hat{\hat{\sigma^2}} = \frac{1}{n} \sum_{i=1}^n (x_i – \hat \mu)^2 \)とすると、
$$ = \left ( \frac{1}{\sqrt{2\pi}} \right )^n \left ( \frac{1}{ \hat{\hat{\sigma^2}}} \right )^{\frac{n}{2}} e^{-\frac{n}{2}} $$
よって尤度比は帰無仮説の確率密度関数と真のパラメータの確率密度関数の比であるから、
$$ \lambda (x) = \frac{f(x_1, \dots , x_n ; \mu_0,\hat{\hat{\sigma^2}} )}{f(x_1, \dots , x_n ; \mu_0,\hat \sigma^2 )} \\
= \frac{\left ( \frac{1}{\sqrt{2\pi}} \right )^n \left ( \frac{1}{ \hat{\hat{\sigma^2}}} \right )^{\frac{n}{2}} e^{-\frac{n}{2}}}{\left ( \frac{1}{\sqrt{2\pi}} \right )^n \left ( \frac{1}{ \hat \sigma^2} \right )^{\frac{n}{2}} e^{-\frac{n}{2}}} \\
= \left ( \frac{ \hat{\hat{\sigma^2}} }{\hat \sigma^2} \right )^{-\frac{n}{2}}$$
となる。
$$\frac{ \hat{\hat{\sigma^2}} }{\hat \sigma^2}= \frac{\frac{1}{n}\sum_{i=1}^n (x_i – \mu_0)^2}{\frac{1}{n}\sum_{i=1}^n(x_i – \bar x)^2}\\
= \frac{ \sum_{i=1}^n \left ( (x_i – \bar x) – (\mu_0 – \bar x ) \right )^2 }{\sum_{i=1}^n(x_i – \bar x)^2} \\
= \frac{ \sum_{i=1}^n (x_i – \bar x)^2 – n(\bar x – \mu_0)^2 }{\sum_{i=1}^n(x_i – \bar x)^2} \\
= 1 + \frac{n(\bar x – \mu_0)^2}{\sum_{i=1}^n(x_i – \bar x)^2} $$
ここで、2項目に注目すると、尤度比は
$$ \lambda (x) < c \\
\Leftrightarrow \frac{n(\bar x – \mu_0)^2}{ \sum_{i=1}^n (x_i – \bar x)^2 } > c’ \\
\Leftrightarrow \frac{\sqrt{n} | \bar x – \mu_0 |}{u} > c” \\
u = \sqrt{ \frac{1}{n-1} \sum_{i=1}^n (x_i – \bar x)^2 }$$
となる。
これは、\( H_0 \)が真のとき、
$$ \frac{\sqrt{n} | \bar x – \mu_0 |}{u} \sim t(n-1) $$
となるため、t分布表から棄却域を得ることができる。
実際、t分布の上側\( \frac{\alpha}{2} \times 100% \)点である、\( t \left (
\frac{\alpha}{2} ; n-1 \right ) \)を求めて、
$$ c” = t \left ( \frac{\alpha}{2} ; n-1 \right ) $$
とおくと、水準\( \alpha \)の尤度比検定の棄却域は
$$ \frac{\sqrt{n} | \bar X – \mu_0 | }{U} > t \left ( \frac{\alpha}{2} ; n-1 \right ) $$
で与えられる。これは両側のt検定に他ならない。
このように尤度比検定は何を検定したいかで最終的に用いる分布が異なる。正規分布のときもあれば、t分布のときもある。
分散に関する検定
$$ H_0 : \sigma = \sigma_0^2 \\
H_1 : \sigma \neq \sigma_0^2 $$
真のパラメータが以下に従うとする。
$$ \hat \mu = \bar x \\
\hat \sigma^2 = \frac{1}{n}\sum_{i=1}^n(x_i – \bar x)^2$$
その際、真のパラメータに従う確率密度関数の最尤解は
$$ \sup_{ (\mu, \sigma^2) \in \Theta } f(x_1, \dots, x_n ; \mu, \sigma^2) = f(x_1, \dots, x_n ; \hat \mu, \hat \sigma^2)\\
= \left ( \frac{1}{\sqrt{2\pi}} \right )^n \left ( \frac{1}{ \hat \sigma^2 } \right )^{\frac{n}{2}} e^{-\frac{n}{2}} $$
他方、帰無仮説に従う確率密度関数の最尤解は
$$ \sup_{ (\mu, \sigma^2) \in \Theta_0 } f(x_1, \dots, x_n ; \mu, \sigma^2) = f(x_1, \dots, x_n ; \hat \mu, \sigma_0^2)\\
= \left ( \frac{1}{\sqrt{2\pi}} \right )^n \left ( \frac{1}{ \sigma_0^2 } \right )^{\frac{n}{2}} e^{-\frac{n \hat \sigma^2}{2\sigma_0^2}} $$
となる。
よって、尤度比は以下のようになる。
$$ \lambda (x) = \frac{f(x_1, \dots, x_n ; \hat \mu, \sigma_0^2) }{f(x_1, \dots, x_n ; \hat \mu, \hat \sigma^2)} \\
= \frac{\left ( \frac{1}{\sqrt{2\pi}} \right )^n \left ( \frac{1}{ \sigma_0^2 } \right )^{\frac{n}{2}} e^{-\frac{n \hat \sigma^2}{2\sigma_0^2}}}{\left ( \frac{1}{\sqrt{2\pi}} \right )^n \left ( \frac{1}{ \hat \sigma^2 } \right )^{\frac{n}{2}} e^{-\frac{n}{2}}} \\
= \left ( \frac{\hat \sigma^2}{\sigma_0^2} \right )^{\frac{n}{2}}e^{-\left ( \frac{\hat \sigma^2}{\sigma_0^2} – 1 \right ) \frac{n}{2} }
$$
これより、定数cについての不等号を記すと、
$$ \lambda (x) < c \\
\Leftrightarrow \log \lambda (x) = – \frac{n}{2} \left \{ \frac{\hat \sigma^2}{\sigma_0^2} – 1 – \log \left ( \frac{\hat \sigma^2}{\sigma_0^2} \right ) \right \} < c’ $$
となる。これは結局のところ、統計検定の棄却域である\( k_1, k_2 \)を定めるように決まるので、以下のようになる。
$$ \frac{\hat \sigma^2}{\sigma_0^2} < k_1 \ or \ \frac{\hat \sigma^2}{\sigma_0^2} > k_2 \\
\frac{1}{\sigma_0^2}\sum_{i=1}^{n}(x_i-\bar x)^2 < k’_1 \ or \ \frac{1}{\sigma_0^2}\sum_{i=1}^{n}(x_i-\bar x)^2 > k’_2
$$
これは\( \chi^2 \)分布であるから、
帰無仮説\( H_0 \)が真のとき、\( \frac{1}{\sigma_0^2}\sum_{i=1}^{n}(x_i-\bar x)^2 \)は\( \chi^2(n-1) \)に従う。
定数\( k’_1,k’_2 \)を
$$ \alpha = \int_{0}^{k’_1}g(x)dx + \int_{k’_2}^{\infty}g(x)dx $$
より求めると、水準\( \alpha \)の尤度比検定の棄却域は
$$ \frac{1}{\sigma_0^2}\sum_{i=1}^{n}(x_i-\bar x)^2 < k’_1 \ or \ \frac{1}{\sigma_0^2}\sum_{i=1}^{n}(x_i-\bar x)^2 > k’_2 $$
で与えられる。棄却限界である\( k’_1,k’_2 \)は近似的に数値解を求めることで得られる。
また、標本数nがある程度大きいとき、尤度比検定に関する定理より、統計量\( -2\log \lambda (x)\)が\( \chi^2 (1) \)に近似的に従うことより、
$$ -2 \log \lambda (x) = n \left \{ \frac{\hat \sigma^2}{\sigma_0^2} – 1 – \log \left ( \frac{\hat \sigma^2}{\sigma_0^2} \right ) \right \} > \chi^2(\alpha ; 1) $$
を棄却域とする検定方法を考えることができる。
尤度比検定(2標本のケース)
（一部数式の導出の解読中）
三つのケースについて扱う。
「A：\( \mu_1, \mu_2 \)は未知、\( \sigma_1^2, \sigma_2^2 \)は既知のケース」
「B：\( \mu_1, \mu_2 \)は未知、\( \sigma_1^2 = \sigma_2^2 = \sigma^2 \)であるが\( \sigma^2 \)の値は未知のケース」
「C：：\( \mu_1, \mu_2, \sigma_1^2, \sigma_2^2 \)の全てが未知のケース」
当然、ケースによって尤度比検定で従う分布が違ってくる。
\( \chi^2 \)適合度検定
ここではサイコロを複数回繰り返し投げたときの出目の出現回数について扱う。各出目の出現総数は多項分布に従うので、以下の確率密度関数を考える。
$$ f(n_1, \dots , n_k ; \theta) = \frac{n!}{n_1! \dots n_k!}\theta_1^{n_1} \dots \theta_k^{n_k} $$
ここでパラメータは以下に従うとする。
$$ \Theta = \left \{ \theta = (\theta_1, \dots, \theta_k) | \sum_{i=1}^k \theta_i = 1 , 0 < \theta_i < 1, i=1, \dots , k
\right \} $$
ここでは以下の検定問題を考える。
$$ H_0 : \theta_i = \theta_{i0} \ , \ i = 1, \dots ,k \\
H_1 : \theta_i \neq \theta_{i0} \ (1 \leq \forall i \leq k) $$
尤度比検定を考える際に、真のパラメータにおける最尤推定量を
$$ \hat \theta_n = ( \hat \theta_{1n}, \dots, \hat \theta_{kn}) \\
= \left ( \frac{n_1}{n},\dots , \frac{n_k}{n} \right ) $$
とする。よって尤度比は
$$ \lambda (n_1, \dots, n_k) = \frac{f(n_1, \dots , n_k ; \theta_0)}{f(n_1, \dots , n_k ; \hat \theta_n)} \\
= \frac{\frac{n!}{n_1! \dots n_k!}\theta_{10}^{n_1} \dots \theta_{k0}^{n_k}}{\frac{n!}{n_1! \dots n_k!}\theta_{1n}^{n_1} \dots \theta_{kn}^{n_k}} \\
= \left ( \frac{\theta_{10}}{\hat \theta_{1n}} \right )^{n_1} \dots \left ( \frac{\theta_{k0}}{\hat \theta_{kn}} \right )^{n_k} $$
となる。
両辺で対数をとり-2を掛けると、
$$ -2 \log \lambda (n_1, \dots , n_k) = 2 \sum_{i=1}^k n_i \{ \log \hat \theta_{in} – \log \theta_{i0} \} $$
この式より、水準\( \alpha \)の尤度比検定の棄却域は、適当な定数cに対して以下の式により与えられる。
$$ -2 \log \lambda (n_1, \dots , n_k) = 2 \sum_{i=1}^k n_i \{ \log \hat \theta_{in} – \log \theta_{i0} \} > c $$
ここで、cは
$$ P_{\theta_{0}} \{ -2 \log \lambda (n_1, \dots, n_k) > c \} = \alpha $$
を満たすように決まる。
$$ -2 \log \lambda (N_1, \dots , N_k) = 2 \sum_{i=1}^k N_i \{ \log \hat \theta_{in} – \log \theta_{i0} \} \\
= 2 \sum_{i=1}^k N_i \log \left ( \frac{\hat \theta_{in}}{\theta_{i0}} \right ) \\
= 2 \sum_{i=1}^k N_i \log \left \{ 1+ \left ( \frac{\hat \theta_{in} – \theta_{i0} }{\theta_{i0}} \right ) \right \} $$
ここでテイラー近似を行うと、
$$ = 2 \sum_{i=1}^k N_i \left \{ \frac{\hat \theta_{in} – \theta_{i0} }{\theta_{i0}} – \frac{ (\hat \theta_{in} – \theta_{i0})^2 }{2\theta_{i0}^2} + O_{p} \left ( | \hat \theta_{in} – \theta_{i0} |^2 \right ) \right \} \\
= 2 \sum_{i=1}^k N_i \left \{ \frac{N_{i} – n \theta_{i0} }{n \theta_{i0}} – \frac{ (N_{i} – n \theta_{i0})^2 }{2n^2\theta_{i0}^2} \right \} + O_{p}(1) \\
= 2 \sum_{i=1}^k N_i \left \{ \frac{ (N_i – n \theta_{i0})^2 + n\theta_{i0}(N_i – n\theta_{i0}) }{n \theta_{i0}} – \frac{(N_i – n\theta_{i0})^3 + n\theta_{i0} (N_i – n \theta_{i0})^2}{2n^2\theta_{i0}^2} \right \} + O_{p}(1) \\
= \sum_{i=1}^k N_i \frac{ (N_i – n \theta_{i0})^2}{n \theta_{i0}} – \sum_{i=1}^k \frac{(N_i – n\theta_{i0})^3}{n^2\theta_{i0}^2} + O_{p}(1) $$
となる。ここで2項目に着目すると、
$$ \sum_{i=1}^{k} \frac{ |N_i – n \theta_{i0}|^3 }{n^2 \theta_{i0}^2} = \sum_{i=1}^{k} \frac{(N_i – n\theta_{i0})^2}{n\theta_{i0}} \cdot \frac{|N_i – n \theta_{i0}|}{n\theta_{i0}} \\
= \sum_{i=1}^{k} \frac{(N_i – n\theta_{i0})^2}{n\theta_{i0}} \cdot \frac{|\hat \theta_{i0} – \theta_{i0}|}{\theta_{i0}} \\
\leq \epsilon_n \cdot \sum_{i=1}^{k} \frac{(N_i – n\theta_{i0})^2}{n\theta_{i0}} $$
となる。ここで、
$$ \epsilon_n = \max_{1 \leq i \leq k} \left \{ \frac{| \hat \theta_{i0} – \theta_{i0} |}{\theta_{i0}} \right \} $$
かつ、
$$ \epsilon_n = O_{p} (1) \ (n \to \infty) $$
であることから、
$$ -2 \log \lambda (N_1, \dots , N_k) = \sum_{i=1}^k N_i \frac{ (N_i – n \theta_{i0})^2}{n \theta_{i0}} + O_{p}(1) $$
が成り立つ。
これは\( \chi^2 \)分布に従うことから、帰無仮説\( H_0 \)のもとで、
$$-2 \log \lambda (N_1, \dots , N_k) $$
は\( n \to \infty \)のとき自由度k-1の\( \chi^2 \)分布に近似的に従う。
よって、
$$ \chi^2 = \sum_{i=1}^k N_i \frac{ (N_i – n \theta_{i0})^2}{n \theta_{i0}} > \chi^2 (\alpha ; k-1) $$
のとき帰無仮説\( H_0 \)を棄却する。このような検定を、水準\( \alpha \times 100% \)の\( \chi^2 \)適合度検定と呼ぶ。これを実際の観測値に置き換えたものを修正\( \chi^2 \)検定と呼び以下のように表す。
$$ \chi_0^2 = \sum_{i=1}^k \frac{(N_i – n \theta_{i0})^2}{N_i} $$
分割表の検定
（更新予定）
（
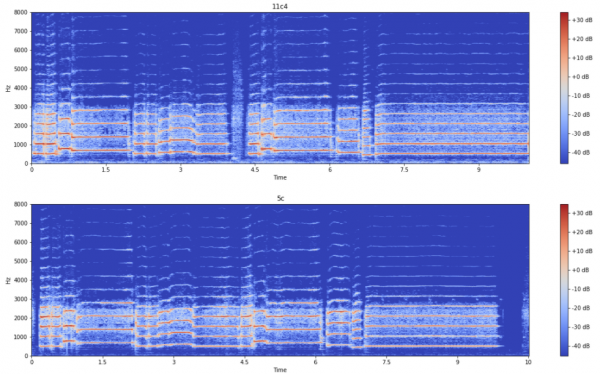
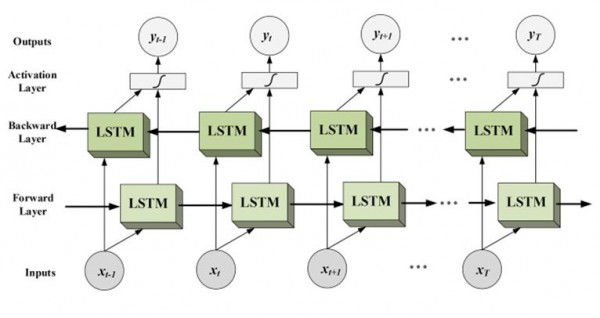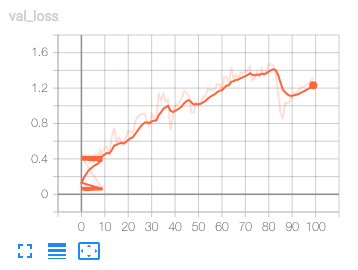エポックに対してloglossが非常に荒れています。学習曲線としてはセオリー的にアウトなようです。一方で、検証のAUCはエポックに従って高まるようです。
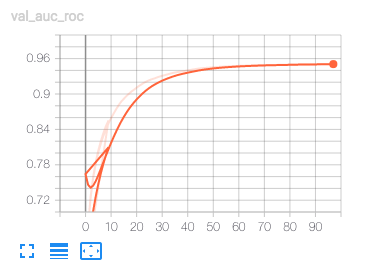AUCは良くなっているけどloglossが増え続けている。loglossが下がらないと過学習している可能性が高いので、これは過学習しているだけなのだろう。
』（岩波書店）
』（コロナ社）
』（共立出版）
』（翔泳社）
』（シーアンドアール研究所）
』（オーム社）
』（技術評論社）
』
』（オライリージャパン）
』
』（朝倉書店）
』（朝倉書店）
』
』（ベレ出版）
』（CCCメディアハウス）
』（北大路書房）
』（共立出版）
』（SBクリエイティブ）
』(オライリー・ジャパン)
』（オライリージャパン）
』（翔泳社）
