A4用紙1枚にまとめるイメージでメモを残そうという取り組みです。
今回は2018年のGoogleのMedia Mix Modeling(マーケティング・ミックス・モデリング)に関する論文です。Bias Correction For Paid Search In Media Mix Modeling前回と違い、因果推論の観点で考察などが書かれています。前回のものがモデリングのテクニカルな側面を描いたものとすると、今回はテクニカルな話は置いておいて、因果関係について様々なケーススタディを扱うというものとなります。
目次
Abstract
1.Introduction and problem description
2.Related work
3.Preliminary to Pearl’s causal theory
4.Methodology
5.Implementation
6.Case studies in simple scenarios
7.Case study with complex scenario
8.Discussion
Abstract
バイアスを回避するようなMedia Mix Modeling(以下、MMM)のモデルの推定について、バックドア基準に基づき、因果ダイアグラムを用いたアプローチをする。
ランダム化実験の結果との比較をすることで推定のバイアスについて考察を行なっている。
シンプルなモデルなら大丈夫だが、複雑なMMMのモデルに関しては不偏推定量は得られていないらしい。
1.Introduction and problem description
・MMMの歴史は長く、1964年のBordenの研究に始まるらしい。
・Fortune500にいるような色々な企業がMMMを試してきたが、課題が色々(データ収集、セレクションバイアス、広告の長期効果、季節性、ファネル効果など)ある。
・ターゲットとしているユーザー群の需要や関心が高まっているとき、広告支出と売上は共に伸びるので、セレクションバイアスが発生する。(実際のところ、儲かっているから広告を打つという場合がありうる。)
・この論文ではMMMにおける検索広告のセレクションバイアスについて扱う。Pearl流の因果推論のアプローチに従い、バックドア基準を満たすようなMMMの推定を行う。
・実験結果と照らし合わせて、不偏推定量がもとまることがわかった。(検索広告に関してだが。)
2.Related work
広告効果の検証などは以下の3つの研究がなされているとのこと。
・1.ユーザー単位のデータを利用して広告を触れたか触れていないかを比較する。傾向スコアなどを計算してマッチングや共変量の調整などを行う。
・2.キャンペーン単位で集計したデータを用いたアプローチで、KPIに関してキャンペーンを打たなかった場合の反事実との比較を行う。
・3.クエリ単位でオーガニック検索とペイド検索をランダムに出し分けてその増分を推定する方法。
この論文で扱うMMMは2つ目のアプローチに近い。違いとしては複数のメディアのキャンペーンを扱うこと。
なお、回帰不連続デザインを用いたケースなどの研究もあるそうな。
3.Preliminary to Pearl’s causal theory
以下のようなDAGを考える。
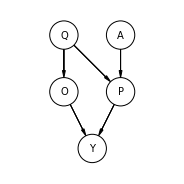
・Aはクエリに関するGoogle広告のオークション
・Qはユーザーの検索するクエリ
・Pはペイド広告でのインプレッション
・Oはオーガニック検索結果
・Yは売上
ようは、 Qが与えられたもとでOが決まり、QとAに影響を受けPが決まり、OとPによってYが決まると言う構図となります。
MMMにおいて広告効果を測るために因果ダイアグラムを理解することは大事と書かれています。
ここではPearl流の因果推論のフレームワークが紹介されています。
$$ X_i = f_i(pa_{i} , \epsilon_i) $$
\( X_i \)は子を表し、\( pa_{i} \)は親を表します。なお、\( f_i \)は関数、\( \epsilon_i \)は任意に決まるランダムな項で他の変数と独立するものとしています。
「因果効果の定義」
二つの変数XとYについて、XのYにおける因果効果は\( Pr(y | \check{x} ) \)で表現できる。Xがxとして与えられたもとで、\( X_i = f_i(pa_{i} , \epsilon_i) \)を解くことで\( Y=y \)の確率を計算できる。ここでの\( \check{x} \)はXをxに設定するという介入を意味している。
「識別性」
ダイアグラムで互換性のある、観測された変数の正の確率から、\( Pr(y | \check{x} ) \)を一意に計算することができるのであれば、XのYにおける因果効果は識別可能となる。
「d-分離」
因果ダイアグラムの二つのノードの間のパスについて、以下の二つの条件のいずれかが満たされる場合についてZノードによって分離されている、あるいはブロックされていると表現する。
・1.\( m \in Z \)として、そのパスが「\( i \to m \to j \)」あるいは、「\( i \gets m \to j \)」を含んでいる。
・2.\( m \notin Z \)として、mがZに依存しないものとして、そのパスが「\( i \to m \gets j \)」を含んでいる。
「バックドア基準」
ダイアグラムにおいて以下の二つを満たす場合、変数Zはバックドア基準を満たす。
・1.変数ZのノードがXの子孫でない。(Xの共変量を除外することに関する基準)
・2.変数ZがXとY(Xへの矢印を含んだもの)の間の全てのパスをブロックしている。(交絡因子の適切な集合をZが含んでいるための基準)
もし、変数Zのバックドア基準が満たされるのであれば、XのYにおける因果効果は以下のように表現することができる。つまりZでXのYにおける因果効果を計算できる。
$$ Pr(Y | \check{x}) = \sum_{z} Pr(Y | x, z) Pr(z) $$
図を再掲しますが、ここでペイド広告の売上への因果効果を知りたいとします。

その場合、QはPの子孫のYを持たないため、バックドア基準の1つ目を満たし、「\( P \gets Q \to O \to Y \)」であることからd分離の条件の1つ目を満たすことからバックドア基準の2つ目を満たす。
つまり、バックドア基準を満たすことから、検索クエリを使うことでペイド広告の売上への因果効果を測れることになります。
Pearl流の因果推論のフレームワークの3つの課題
・1.因果ダイアグラムをどう構築するのか?
・2.全ての必要な変数を正確に観測、計測することができるのか?
・3.識別が可能だとして、有限であるサンプルサイズにおいて、\( Pr(Y | X, Z) \)の関数系はどうなるか?
広告まわりのデータは潤沢にデータがあるわけではないし計測できないものもあるため、どの課題も無視できない。
4.Methodology
「シンプルなシナリオ」
売上への他のメディアの貢献は無視できるものとして、広告のみをチャネルとして想定する。
$$Y_{t}=\beta_0 + \beta_1 X_t + \epsilon_t$$
\( X_t \)はあるプロダクトの検索広告の支出、\( Y_t \)はあるプロダクトの売上。\( \beta_1 \)は広告の売り上げにもたらす効果でROASと呼ばれる、\( \epsilon_t \)は\( X_t \)では説明づけることができなかった売上への影響を指す。計量経済学などで問題として扱われる内生性はこの\( \epsilon_t \)と\( X_t \)の相関によって起きる。
実際に、\( \epsilon \)がXと相関するとして式を変形すれば、不偏推定ができないことがわかります。
ここで、潜在的にプロダクトの売上に影響を与える検索クエリを集約した\(V\)という統計量を考えます。
誤差項\( \epsilon \)が以下のように、オーガニックサーチによる影響(\( \epsilon_1 \))と経済要因(\( \epsilon_0 \))によるものからなるとします。
$$ \epsilon = \epsilon_0 + \epsilon_1 $$
ここで、
$$ \epsilon_1 \perp X | V $$
や
$$ \epsilon_0 \perp X | V $$
を満たすようなVを見つけることができれば、因果効果を測れることになります。
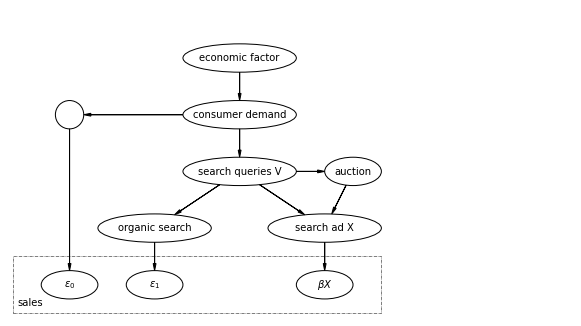
※想定1:検索広告の予算はないとする。
※想定2:検索クエリで条件付けした際に、広告主の入札や競合の行動の影響は無視できる。
理論1
ペイド広告ついて上の図を想定した際に、XとY(sales)が完全に相関していないならば、正則化条件のもとで、検索広告のROAS(\( \beta_1 \))を推定することができる。
$$Y = \beta_0 + \beta_1 X + f(V) + \eta$$
ここで\( f(\cdot) \)は未知の関数、\( \eta\)はXや\(f(V)\)と相関しない残差とします。
上の図において、変数ZのノードがXの子孫でないというバックドア基準の一つ目はクリアしていることは明らかで、d分離の観点に関しても一つ目を満たしているためブロックしているため、バックドア基準の二つ目もクリアしている。
$$ E(Y | X, V) = \beta_0 + \beta_1 X + E(\epsilon | X, V)$$
Vで条件付けるとXは誤差項と直交することから、
$$E(\epsilon|X,V)=E(\epsilon|V)$$
となり、
$$ E(Y | X, V) = \beta_0 + \beta_1 X + f(V) $$
と表すことができる。
この式で回帰分析をすることでROASである\(\beta_1\)を推定することができる。
「複雑なシナリオ」
ここでは検索広告以外(\( X_2 \))も売上に影響を与えるというケースを扱っています。
まず、予算に関して検索広告と検索広告以外の広告(\( X_2 \))の両方に制約がある場合を考えます。以下の図が、今回のダイアグラムですが、先程の図に予算が追加されていることがわかります。
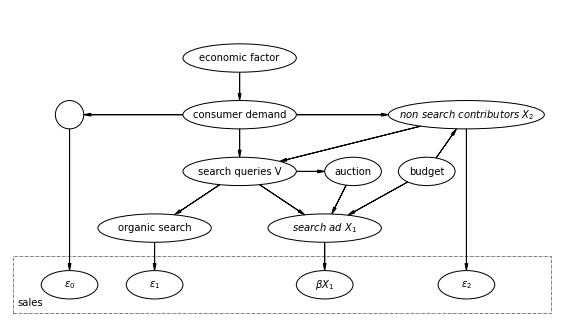
なお、ここでは広告のヒストリカルな影響などの複雑さは考慮していません。
一方で、予算が検索広告に関しては制約となっていないケースだと以下のダイアグラムになります。
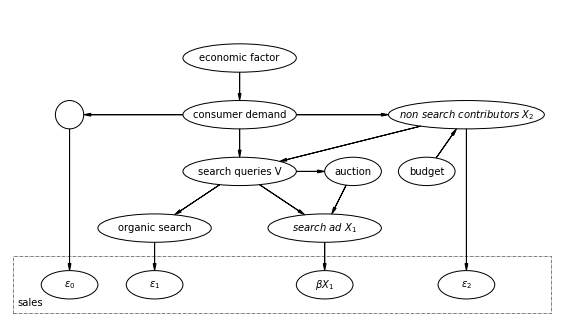
理論2
1.広告予算が検索広告に制約を設けているケースで、広告のラグ効果が無視できるとして、もし\(X_1\)が\(V\)や\(X_2\)と完全に相関しておらず、正則化条件を満たすなら検索広告のROAS(\( \beta_1 \))は以下の回帰モデルで推定することができる。
$$ Y = \beta_0 + \beta_1 X_1 + f(V, X_2) + \eta$$
ここで
となり、\( \eta\)は残差で\(X_1\)と\(f(V,X_2)\)と相関しない。
ダイアグラムを再掲します。

2.広告予算が検索広告に制約を設けていないケースで、正則化条件を満たすなら検索広告のROAS(\( \beta_1 \))は以下の回帰モデルで推定することができる。
$$Y = \beta_0 + \beta_1 X_1 + f(V) + \eta$$
ここでfは未知の関数とする。
ダイアグラムを再掲します。

以上、因果ダイアグラムを描き、バックドア基準を満たしバイアスのないパラメータ推定をするということが書かれていました。
ここではシンプルに特定の広告の効果を見ていましたが、MMMにおいては複数のメディアの効果を求めなければならないです。
考えられるアプローチとしては、最初にバイアス補正を行い\( X_1 \)の影響を推定し、それを使って\( X_2 \)を推定するというもの。
5.Implementation
・検索クエリのデータの集計の仕方
・STEP1:広告主と競合のサイトを識別する。
・STEP2:特定のエリアで自然検索でURLが見つかる回数をカウントする。
・STEP3:クエリを3つのグループに分類。おのおの閾値を設ける。
・STEP4:クエリをグループごとに分けたものを推定の際に誤差項と直交するものとして扱う。(閾値は50%がいいらしい。)
・TBA
6.Case studies in simple scenarios
・ナイーブな推定手法では過大に効果を推定していることがわかった。
・需要による調整だけではバイアスを十分にとりきれないことがわかった。
・SBC(search bias correction)の手法によりROASがランダム化実験の結果に近くなった。
・TBA
7.Case study with complex scenario
・TBA
・TBA
・TBA
8.Discussion
・TBA
・TBA
・TBA