強化学習 – かものはしの分析ブログ

はじめに

このブログの私の中での位置づけは、今後仕事で使いそうなものを調べて書き溜めるというところにあります。仕事で使っているものはブログに載せないというスタンスでもあるのですが、出来るだけ先回りしておきたいところです。今回は、昨年のJapan.RやTokyo.Rで紹介されていたcontextualパッケージを触ってみたというゆるふわな内容となっています。

・バンディット問題とは
・マーケティング関連でバンディット問題が役に立つ場面
・バンディット問題で出てくる数学的な知識と方策
・Contextual Bandit問題とは
・Contextualパッケージでできること
・サンプル実行
・おわりに
・参考情報

バンディット問題とは

「選択肢の集合から1つの要素を選択して、その選択肢に対する報酬を得るものの、他の選択肢の報酬情報は得られないというプロセスを繰り返す設定において、報酬の合計値を最大化することを目指す逐次決定問題」とされています。バンディットは昔ながらのスロットマシンが客からお金をむしり取ること（盗賊）にちなんでいるそうです。胴元は盗賊ということなんでしょうか？

大学時代の知人は毎日パチンコ屋に行ってから講義に行っていましたが、出そうな台・出そうな店を転々としていましたが、あれはバンディット問題を彼なりに解いていたのでしょう。当時はサクラの台というのがあったらしく、3000円ほど投資すれば大当たりになるのだとか。そしてその大当たりに釣られて他の客が頑張るという意味で、サクラの台だそうです。

マーケティング関連でバンディット問題が役に立つ場面

私はマーケティング×データ分析を生業としているので、マーケティング方面にしか関心がないのですが、バンディット問題は役立つ可能性が十分にあるというか既に一部の企業ではバリューを出しています。

・インターネット広告配信：オレシカナイトでSpeeeの方がトンプソン抽出で精度を増していた。
・推薦システムにおけるコールドスタート問題：ネットフリックスが情報推薦の際にContextual Banditを適用

バンディット問題とは異なるものの、最適腕識別問題においては、クックパッドのクリエイティブ出し分けやGoogleのウェブテスト（旧Webサイトオプティマイザー）などで使われています。ちなみに、バンディット問題と最適腕識別問題は似て非なるものであるということを『バンディット問題の理論とアルゴリズム』で知りました。

また、マーケティングとは違いますが、株価のトレーディングの際にバンディットアルゴリズムを使っているという事例（Bandits and Stocks）が当然ながらあるようです。

バンディット問題で出てくる数学的な知識と方策

バンディット問題の書籍を読もうとすると、数理統計学の知識が必要です。

あるスロットを何回引くべきかという意思決定の際に、「神のみぞ知る真の報酬」と「あるスロットの報酬」がどれくらい外れているか、そしてそのハズレ具合は許容できるのかということが重要になります。
「神のみぞ知る真の報酬と、あるスロットの報酬がΔだけ外れている確率」の推論の精度に関心があるということです。

バンディット問題において、「その時のベストのスロットを引いた際のリターン」と「その時実際に選んだスロットのリターン」の差の期間合計値をリグレットとして、そのリグレットを小さくするようにスロットを選びます。
そのリグレットに対して理論的な下限を求める際に、数理統計学の知識が必要になります。

具体的には、ヘフディングの不等式、その前提となるマルコフの不等式やチェビシェフの不等式やチェルノフ限界、積率母関数やイェンセンの不等式などです。
それらを駆使しながら、様々な施策の中で、理論的な下限がより小さくなるようなものを探そうという流れのようです。

『バンディット問題の理論とアルゴリズム』を読む上で前提となっていそうな知識として、スタンフォード大学の講義資料（CS229 Supplemental Lecture notes Hoeffding’s inequality）を運良く見つけることが出来たので、これをもとに学ぶと理解が捗ると思います。

リグレットの下限を低めることを目指して、様々なアプローチが議論されます。

ε-貪欲法

概要：スロットを回す回数のうち、一定割合（ε）をスロットの探索に当て、残りの期間を良いとされるスロットを回し続ける。
メリット：実装が容易でシステムに組み込み易い
デメリット：期待値が悪いスロットも良いスロットも同じ回数引いてしまうので性能が悪くなる。スロットの種類が多い際はより一層悪くなりやすい。

UCB(Upper Confidence Bound)方策

概要：標本平均に補正項を足した、UCBスコアを各時点ごとに計算し、最もスコアが高いスロットを回す。なお、補正項は選択回数の少ないスロットに対して大きくなります。
メリット：ε-貪欲法と異なり、リグレットの上限がεなどの水準に左右されない。ハイパーパラメータが少ない。
デメリット：真の期待値についての信頼区間を求めることは本質的ではない。

KL-UCB

概要：KLダイバージェンスを用いてUCBスコアを計算し、最もスコアが高いスロットを回す。
メリット：KLダイバージェンスを様々なモデルに応じて置き換えることができるなど、柔軟性がある。
デメリット：KLダイバージェンスの逆関数を計算する必要があり、毎回ニュートン法などを適用する必要がある。

MED(Minimum Empirical Divergence)方策

概要：期待値最大である際の尤度が一定以上のスロットを回すという方策。
メリット：KLダイバージェンスの逆関数を計算する必要がない。
デメリット：KL-UCBよりも性能が悪い。IMEDという方策であればその弱点を克服している。

トンプソン抽出

概要：期待値最大でないスロットの選択数の期待値を近似的に最小化するという取り組みを、ベイズ統計の枠組みで行ったもの。
メリット：経験的に高い性能となりやすい。
デメリット：？

Contextual Bandit問題とは

ある時点のあるスロットの報酬が、ユーザーの特徴量と誤差項により線形で表すことができるものを、線形バンディットと呼びます。
ユーザーの各行動の特徴量が時刻により異なる値を取ることを許すという設定を、文脈付きバンディット（Contextual Bandit）と呼びます。
つまり、Contextual Banditは時刻により異なるユーザーの特徴量が与えられたもとでの、利得の期待値の最大化問題となります。

具体的には、パチンコ店における期待値最大化の行動を考えるとすると、パチンコ台の大当たり確率は、午前か午後か、大当たりが既に他の台で出たか、その台がどれくらい回されているかなどの時間による文脈に左右されるという状況となります。

このContextual Banditにおいても、先程あげたようなリグレットを最小にするような様々な方策があります。LinUCB方策や、線形モデルのトンプソン抽出、ロジスティック回帰モデルのバンディットなどです。

Contextualパッケージでできること

こちらの資料にある通り、バンディットアルゴリズムのシミュレーションとオフライン評価が行えるパッケージです。
多様なバンディットアルゴリズムを試すことができます。
要となるデータですが、シミュレーションにより生成することもできれば、過去にランダムに出し分けたログなどのデータがあればそのデータをもとにアルゴリズムの検証をすることができます。

サンプル実行

さて、今回は完全に手抜きです。GitHubにあったサンプルコードを3つほど回すだけです。ただ、特徴量の突っ込み方などをサンプルコードから学べるので、ぜひ開発者のGitHubをご覧ください。

サンプル1：ABテストによる最適腕選択

パッケージのGitHub
にコードがありました。Bandit Algorithms for Website Optimizationという書籍に登場してきている例をRで実行できるサンプルです。
・ε-貪欲法を様々なεでシミュレーションして最適なスロットを見つける
・ソフトマックスによる方策に関しても様々なτに応じたシミュレーションをして最適なスロットを見つける
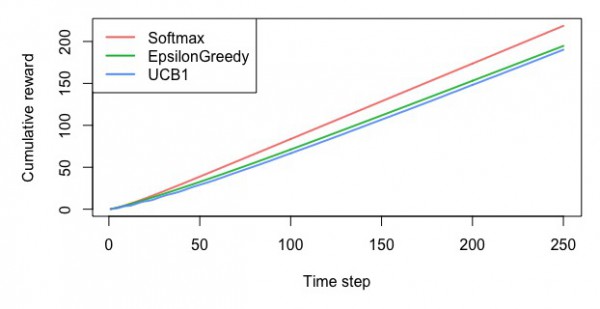
・UCB方策によりシミュレーションを行い、最適なスロットを見つける。ε-貪欲法やソフトマックスとの比較を行う
という実験ができます。シミュレーションの設定として、スロットごとの当たりの出る確率をベクトルで指定しています。

実行するのに10分くらいはかかるかもしれません。

library(contextual)

# Bandit algorithms for website optimization -----------------------------------------------------------------

## Simulation of the multi-armed Bandit examples in
## of "Bandit algorithms for website optimization"
## by John Miles White.

# The code from the book chooses the arm with the first index when all arms are equal.
# Contextuals policies correctly picks one of the max arms.
# That's why the plots below are slightly different from the book - they are correct, though.

# Chapter 4 - Debugging and epsilon greedy -------------------------------------------------------------------

prob_per_arm       <- c(0.1, 0.1, 0.1, 0.1, 0.9)
horizon            <- 250
simulations        <- 5000

bandit             <- BasicBernoulliBandit$new(prob_per_arm)

agents             <- list(Agent$new(EpsilonGreedyPolicy$new(0.1), bandit, "Epsilon = 0.1"),
                           Agent$new(EpsilonGreedyPolicy$new(0.2), bandit, "Epsilon = 0.2"),
                           Agent$new(EpsilonGreedyPolicy$new(0.3), bandit, "Epsilon = 0.3"),
                           Agent$new(EpsilonGreedyPolicy$new(0.4), bandit, "Epsilon = 0.4"),
                           Agent$new(EpsilonGreedyPolicy$new(0.5), bandit, "Epsilon = 0.5"))

simulation         <- Simulator$new(agents, horizon, simulations)
history            <- simulation$run()

# Figure 4-2. How often does the epsilon greedy algorithm select the best arm?

plot(history, type = "optimal", legend_position = "bottomright", ylim = c(0,1))

# Figure 4-3. How much reward does the epsilon greedy algorithm earn on average?

plot(history, type = "average", regret = FALSE, legend_position = "bottomright", ylim = c(0,1))

# Figure 4-4. How much reward has the epsilon greedy algorithm earned by trial t?

plot(history, type = "cumulative", regret = FALSE)

# Chapter 5 - Softmax ----------------------------------------------------------------------------------------

agents             <- list(Agent$new(SoftmaxPolicy$new(0.1), bandit, "Tau = 0.1"),
                           Agent$new(SoftmaxPolicy$new(0.2), bandit, "Tau = 0.2"),
                           Agent$new(SoftmaxPolicy$new(0.3), bandit, "Tau = 0.3"),
                           Agent$new(SoftmaxPolicy$new(0.4), bandit, "Tau = 0.4"),
                           Agent$new(SoftmaxPolicy$new(0.5), bandit, "Tau = 0.5"))

simulation         <- Simulator$new(agents, horizon, simulations)
history            <- simulation$run()

# Figure 5-2. How often does the softmax algorithm select the best arm?

plot(history, type = "optimal", legend_position = "bottomright", ylim = c(0,1))

# Figure 5-3. How much reward does the softmax algorithm earn on average?

plot(history, type = "average", regret = FALSE, legend_position = "bottomright", ylim = c(0,1))

# Figure 5-4. How much reward has the softmax algorithm earned by trial t?

plot(history, type = "cumulative", regret = FALSE)


# Chapter 6 - UCB --------------------------------------------------------------------------------------------

agents             <- list(Agent$new(SoftmaxPolicy$new(0.1), bandit, "Softmax"),
                           Agent$new(EpsilonGreedyPolicy$new(0.1), bandit, "EpsilonGreedy"),
                           Agent$new(UCB1Policy$new(), bandit, "UCB1"))

simulation         <- Simulator$new(agents, horizon, simulations)
history            <- simulation$run()

# Figure 6-3. How often does the UCB algorithm select the best arm?

plot(history, type = "optimal", legend_position = "bottomright", ylim = c(0,1))

# Figure 6-4. How much reward does the UCB algorithm earn on average?

plot(history, type = "average", regret = FALSE, legend_position = "bottomright", ylim = c(0,1))

# Figure 6-5. How much reward has the UCB algorithm earned by trial t?

plot(history, type = "cumulative", regret = FALSE)

library(contextual)

# Bandit algorithms for website optimization -----------------------------------------------------------------

## Simulation of the multi-armed Bandit examples in

## of "Bandit algorithms for website optimization"

## by John Miles White.

# The code from the book chooses the arm with the first index when all arms are equal.

# Contextuals policies correctly picks one of the max arms.

# That's why the plots below are slightly different from the book - they are correct, though.

# Chapter 4 - Debugging and epsilon greedy -------------------------------------------------------------------

prob_per_arm <- c(0.1, 0.1, 0.1, 0.1, 0.9)

horizon <- 250

simulations <- 5000

bandit <- BasicBernoulliBandit$new(prob_per_arm)

agents <- list(Agent$new(EpsilonGreedyPolicy$new(0.1), bandit, "Epsilon = 0.1"),

Agent$new(EpsilonGreedyPolicy$new(0.2), bandit, "Epsilon = 0.2"),

Agent$new(EpsilonGreedyPolicy$new(0.3), bandit, "Epsilon = 0.3"),

Agent$new(EpsilonGreedyPolicy$new(0.4), bandit, "Epsilon = 0.4"),

Agent$new(EpsilonGreedyPolicy$new(0.5), bandit, "Epsilon = 0.5"))

simulation <- Simulator$new(agents, horizon, simulations)

history <- simulation$run()

# Figure 4-2. How often does the epsilon greedy algorithm select the best arm?

plot(history, type = "optimal", legend_position = "bottomright", ylim = c(0,1))

# Figure 4-3. How much reward does the epsilon greedy algorithm earn on average?

plot(history, type = "average", regret = FALSE, legend_position = "bottomright", ylim = c(0,1))

# Figure 4-4. How much reward has the epsilon greedy algorithm earned by trial t?

plot(history, type = "cumulative", regret = FALSE)

# Chapter 5 - Softmax ----------------------------------------------------------------------------------------

agents <- list(Agent$new(SoftmaxPolicy$new(0.1), bandit, "Tau = 0.1"),

Agent$new(SoftmaxPolicy$new(0.2), bandit, "Tau = 0.2"),

Agent$new(SoftmaxPolicy$new(0.3), bandit, "Tau = 0.3"),

Agent$new(SoftmaxPolicy$new(0.4), bandit, "Tau = 0.4"),

Agent$new(SoftmaxPolicy$new(0.5), bandit, "Tau = 0.5"))

simulation <- Simulator$new(agents, horizon, simulations)

history <- simulation$run()

# Figure 5-2. How often does the softmax algorithm select the best arm?

plot(history, type = "optimal", legend_position = "bottomright", ylim = c(0,1))

# Figure 5-3. How much reward does the softmax algorithm earn on average?

plot(history, type = "average", regret = FALSE, legend_position = "bottomright", ylim = c(0,1))

# Figure 5-4. How much reward has the softmax algorithm earned by trial t?

plot(history, type = "cumulative", regret = FALSE)

# Chapter 6 - UCB --------------------------------------------------------------------------------------------

agents <- list(Agent$new(SoftmaxPolicy$new(0.1), bandit, "Softmax"),

Agent$new(EpsilonGreedyPolicy$new(0.1), bandit, "EpsilonGreedy"),

Agent$new(UCB1Policy$new(), bandit, "UCB1"))

simulation <- Simulator$new(agents, horizon, simulations)

history <- simulation$run()

# Figure 6-3. How often does the UCB algorithm select the best arm?

plot(history, type = "optimal", legend_position = "bottomright", ylim = c(0,1))

# Figure 6-4. How much reward does the UCB algorithm earn on average?

plot(history, type = "average", regret = FALSE, legend_position = "bottomright", ylim = c(0,1))

# Figure 6-5. How much reward has the UCB algorithm earned by trial t?

plot(history, type = "cumulative", regret = FALSE)

ε-貪欲法

・最適なスロットを選んだ確率

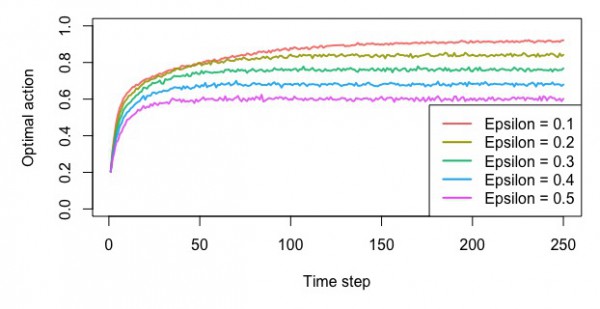
・平均報酬額

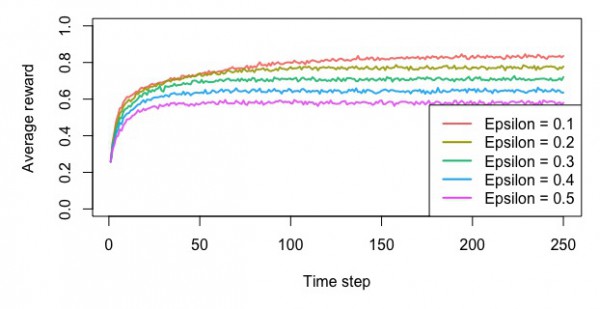
　・累積報酬額

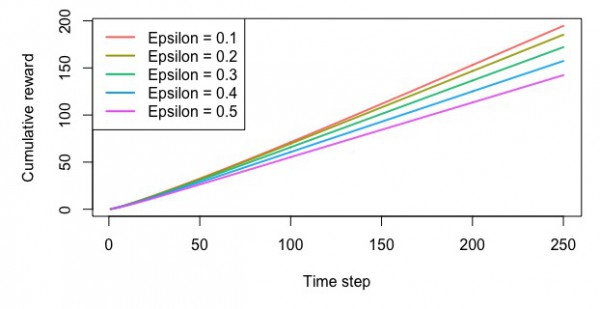
ソフトマックスによる方策

・最適なスロットを選んだ確率

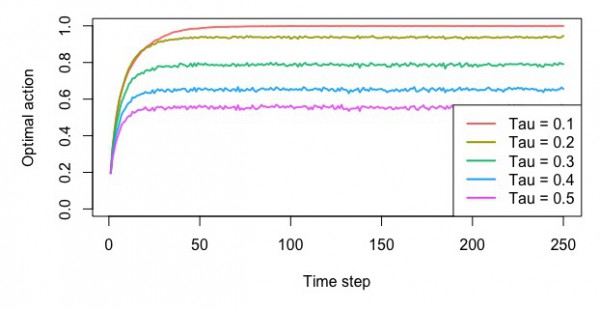
・平均報酬額

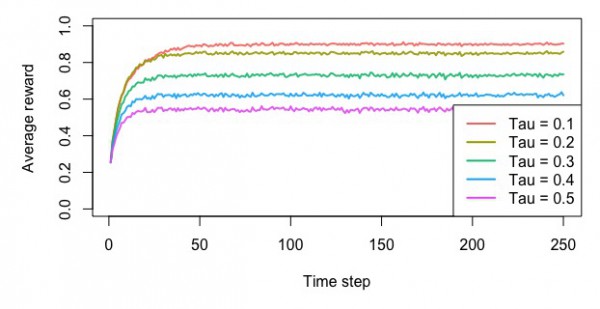
・累積報酬額

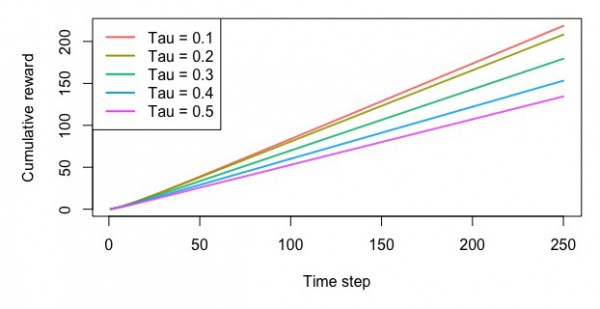
UCB方策

・最適なスロットを選んだ確率

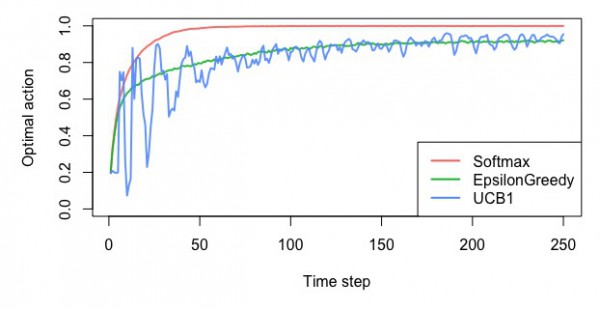
・平均報酬額

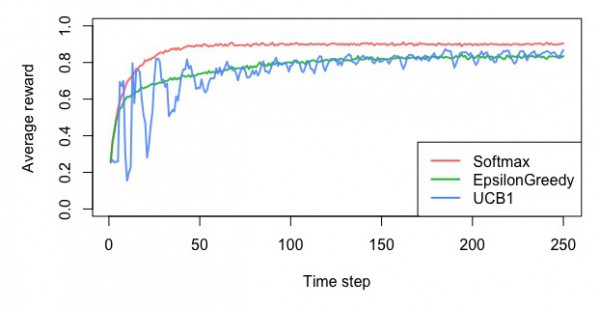
・累積報酬額

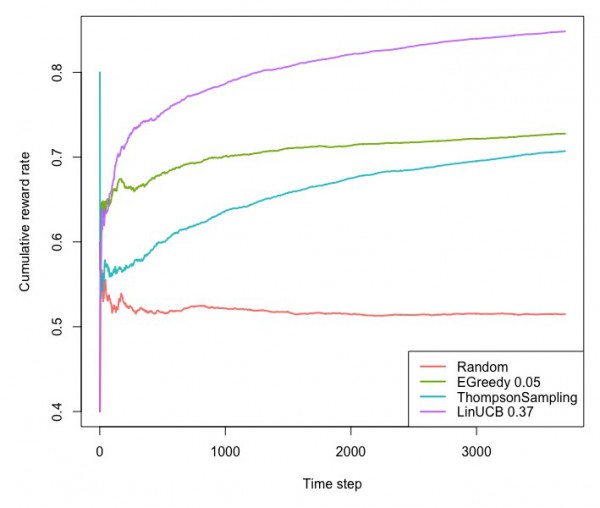
サンプル2：文脈付きバンディット問題で映画のレーティングの最適化

同じGitHubにあるこちらのコードは、映画のデータセットに対して、文脈付きバンディット問題でオフラインテストをするためのコードです。映画のレーティングが4以上なら1そうでないなら0のデータを作り、特徴量として映画館で見たか家で見たか、一人で見たか家族と見たか、週末に見たかどうかなどの変数を7個ほど作成しています。方策としては、ランダムなもの、ε-貪欲法、トンプソン抽出、LinUCBをシミュレーションしています。

実行してから処理が止まるまで1時間程度はかかりましたが、LinUCBが累積の報酬が大きいようです。

library(contextual)
library(data.table)

# Import personalization data-set

# Info: https://d1ie9wlkzugsxr.cloudfront.net/data_irecsys_CARSKit/Movie_DePaulMovie/README.txt

url         <- "http://d1ie9wlkzugsxr.cloudfront.net/data_irecsys_CARSKit/Movie_DePaulMovie/ratings.csv"
data        <- fread(url, stringsAsFactors=TRUE)

# Convert data

data        <- contextual::one_hot(data, cols = c("Time","Location","Companion"), sparsifyNAs = TRUE)
data[, itemid := as.numeric(itemid)]
data[, rating := ifelse(rating <= 3, 0, 1)]

# Set simulation parameters.
simulations <- 10  # here, "simulations" represents the number of boostrap samples
horizon     <- nrow(data)

# Initiate Replay bandit with 10 arms and 100 context dimensions
log_S       <- data
formula     <- formula("rating ~ itemid | Time_Weekday + Time_Weekend + Location_Cinema + Location_Home +
                                          Companion_Alone + Companion_Family + Companion_Partner")
bandit      <- OfflineBootstrappedReplayBandit$new(formula = formula, data = data)

# Define agents.
agents      <-
  list(Agent$new(RandomPolicy$new(), bandit, "Random"),
       Agent$new(EpsilonGreedyPolicy$new(0.03), bandit, "EGreedy 0.05"),
       Agent$new(ThompsonSamplingPolicy$new(), bandit, "ThompsonSampling"),
       Agent$new(LinUCBDisjointOptimizedPolicy$new(0.37), bandit, "LinUCB 0.37"))

# Initialize the simulation.
simulation  <-
                Simulator$new(
                  agents           = agents,
                  simulations      = simulations,
                  horizon          = horizon
                )

# Run the simulation.
# Takes about 5 minutes: bootstrapbandit loops for arms x horizon x simulations (times nr of agents).
sim  <- simulation$run()

# plot the results
plot(sim, type = "cumulative", regret = FALSE, rate = TRUE,
     legend_position = "topleft", ylim=c(0.48,0.87))

library(contextual)

library(data.table)

# Import personalization data-set

# Info: https://d1ie9wlkzugsxr.cloudfront.net/data_irecsys_CARSKit/Movie_DePaulMovie/README.txt

url <- "http://d1ie9wlkzugsxr.cloudfront.net/data_irecsys_CARSKit/Movie_DePaulMovie/ratings.csv"

data <- fread(url, stringsAsFactors=TRUE)

# Convert data

data <- contextual::one_hot(data, cols = c("Time","Location","Companion"), sparsifyNAs = TRUE)

data[, itemid := as.numeric(itemid)]

data[, rating := ifelse(rating <= 3, 0, 1)]

# Set simulation parameters.

simulations <- 10 # here, "simulations" represents the number of boostrap samples

horizon <- nrow(data)

# Initiate Replay bandit with 10 arms and 100 context dimensions

log_S <- data

formula <- formula("rating ~ itemid | Time_Weekday + Time_Weekend + Location_Cinema + Location_Home +

Companion_Alone + Companion_Family + Companion_Partner")

bandit <- OfflineBootstrappedReplayBandit$new(formula = formula, data = data)

# Define agents.

agents <-

list(Agent$new(RandomPolicy$new(), bandit, "Random"),

Agent$new(EpsilonGreedyPolicy$new(0.03), bandit, "EGreedy 0.05"),

Agent$new(ThompsonSamplingPolicy$new(), bandit, "ThompsonSampling"),

Agent$new(LinUCBDisjointOptimizedPolicy$new(0.37), bandit, "LinUCB 0.37"))

# Initialize the simulation.

simulation <-

Simulator$new(

agents = agents,

simulations = simulations,

horizon = horizon

)

# Run the simulation.

# Takes about 5 minutes: bootstrapbandit loops for arms x horizon x simulations (times nr of agents).

sim <- simulation$run()

# plot the results

plot(sim, type = "cumulative", regret = FALSE, rate = TRUE,

legend_position = "topleft", ylim=c(0.48,0.87))

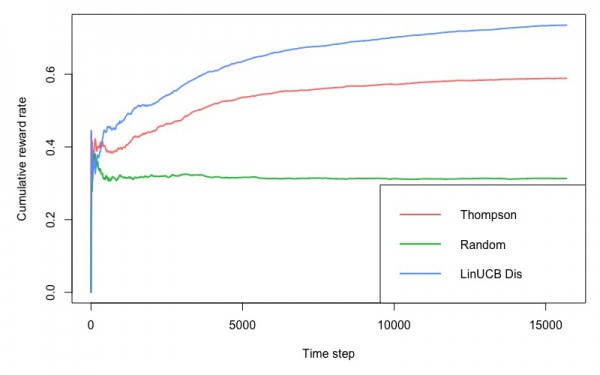
サンプル3：文脈付きバンディット問題でMovieLensのTop50の作品における評価の最適化

こちらのコードは、MovieLensのデータセットにおいて、特徴量として過去にユーザーが評価した映画のカテゴリーの割合を19カテゴリ分用意して、ユーザーの見た映画の評価を最も高めるという、文脈付きバンディット問題です。こちらは実行して、30分程度で処理が終わりました。先程のサンプルと同じで、LinUCBが累積の報酬が大きいようです。

library(contextual)
library(data.table)
library(splitstackshape)

# Movielens 100k ---------------------------------------------------------------------------------------------

# Info: https://d1ie9wlkzugsxr.cloudfront.net/data_movielens/ml-100k/ml-100k-README.txt

movies_dat      <- "http://d1ie9wlkzugsxr.cloudfront.net/data_movielens/ml-100k/u.item"
ratings_dat     <- "http://d1ie9wlkzugsxr.cloudfront.net/data_movielens/ml-100k/u.data"

# Import and merge files

movies_dat      <- fread(movies_dat, sep = "|", quote="")
setnames(movies_dat, c("V1", "V2"), c("MovieID", "Name"))
movies_dat[, (3:5)  := NULL ]
ratings_dat     <- fread(ratings_dat, quote="")
setnames(ratings_dat, c("V1", "V2", "V3", "V4"), c("UserID", "MovieID", "Rating", "Timestamp"))
all_movies      <- ratings_dat[movies_dat, on=c(MovieID = "MovieID")]

rm(movies_dat,ratings_dat)

# Data wrangling ---------------------------------------------------------------------------------------------

count_movies    <- all_movies[,.(MovieCount = .N), by = MovieID]
top_50          <- as.vector(count_movies[order(-MovieCount)][1:50]$MovieID)
not_50          <- as.vector(count_movies[order(-MovieCount)][51:nrow(count_movies)]$MovieID)
top_50_movies   <- all_movies[MovieID %in% top_50]

# User features: tags they've watched for non-top-50 movies normalized per user

user_features   <- all_movies[MovieID %in% not_50]
rm(all_movies)
user_features[, c("MovieID", "Rating", "Timestamp", "Name"):=NULL]
user_features   <- user_features[, lapply(.SD, sum, na.rm=TRUE), by=UserID ]
user_features[, total := rowSums(.SD, na.rm = TRUE), .SDcols = 2:20]
user_features[, 2:20 := lapply(.SD, function(x) x/user_features$total), .SDcols = 2:20]
user_features$total <- NULL

# Add user features to top50
top_50_movies      <- top_50_movies[user_features, on=c(UserID = "UserID")]
top_50_movies      <- na.omit(top_50_movies)

rm(user_features, not_50, top_50, count_movies)

top_50_movies[, choice := as.numeric(as.factor(MovieID))]
top_50_movies[, reward := ifelse(Rating <= 4, 0, 1)]

# Run simulation ---------------------------------------------------------------------------------------------

simulations <- 1
horizon     <- nrow(top_50_movies)

formula     <- formula("reward ~ choice | i.V6 + i.V7 + i.V8 +i.V9 + i.V10 + i.V11 + i.V12 + i.V13 + i.V14 +
                                          i.V15 + i.V16 + i.V17 + i.V18 + i.V19 + i.V20 + i.V21 + i.V22 +
                                          i.V23 + i.V24")

bandit      <- OfflineBootstrappedReplayBandit$new(formula = formula, data = top_50_movies)

agents      <-
  list(Agent$new(ThompsonSamplingPolicy$new(), bandit, "Thompson"),
       Agent$new(RandomPolicy$new(), bandit, "Random"),
       Agent$new(LinUCBDisjointOptimizedPolicy$new(2.05), bandit, "LinUCB Dis"))

simulation  <-
  Simulator$new(
    agents           = agents,
    simulations      = simulations,
    horizon          = horizon
  )

sim  <- simulation$run()

plot(sim,
     type = "cumulative",
     regret = FALSE,
     rate = TRUE,
     legend_position = "bottomright")

library(contextual)

library(data.table)

library(splitstackshape)

# Movielens 100k ---------------------------------------------------------------------------------------------

# Info: https://d1ie9wlkzugsxr.cloudfront.net/data_movielens/ml-100k/ml-100k-README.txt

movies_dat <- "http://d1ie9wlkzugsxr.cloudfront.net/data_movielens/ml-100k/u.item"

ratings_dat <- "http://d1ie9wlkzugsxr.cloudfront.net/data_movielens/ml-100k/u.data"

# Import and merge files

movies_dat <- fread(movies_dat, sep = "|", quote="")

setnames(movies_dat, c("V1", "V2"), c("MovieID", "Name"))

movies_dat[, (3:5) := NULL ]

ratings_dat <- fread(ratings_dat, quote="")

setnames(ratings_dat, c("V1", "V2", "V3", "V4"), c("UserID", "MovieID", "Rating", "Timestamp"))

all_movies <- ratings_dat[movies_dat, on=c(MovieID = "MovieID")]

rm(movies_dat,ratings_dat)

# Data wrangling ---------------------------------------------------------------------------------------------

count_movies <- all_movies[,.(MovieCount = .N), by = MovieID]

top_50 <- as.vector(count_movies[order(-MovieCount)][1:50]$MovieID)

not_50 <- as.vector(count_movies[order(-MovieCount)][51:nrow(count_movies)]$MovieID)

top_50_movies <- all_movies[MovieID %in% top_50]

# User features: tags they've watched for non-top-50 movies normalized per user

user_features <- all_movies[MovieID %in% not_50]

rm(all_movies)

user_features[, c("MovieID", "Rating", "Timestamp", "Name"):=NULL]

user_features <- user_features[, lapply(.SD, sum, na.rm=TRUE), by=UserID ]

user_features[, total := rowSums(.SD, na.rm = TRUE), .SDcols = 2:20]

user_features[, 2:20 := lapply(.SD, function(x) x/user_features$total), .SDcols = 2:20]

user_features$total <- NULL

# Add user features to top50

top_50_movies <- top_50_movies[user_features, on=c(UserID = "UserID")]

top_50_movies <- na.omit(top_50_movies)

rm(user_features, not_50, top_50, count_movies)

top_50_movies[, choice := as.numeric(as.factor(MovieID))]

top_50_movies[, reward := ifelse(Rating <= 4, 0, 1)]

# Run simulation ---------------------------------------------------------------------------------------------

simulations <- 1

horizon <- nrow(top_50_movies)

formula <- formula("reward ~ choice | i.V6 + i.V7 + i.V8 +i.V9 + i.V10 + i.V11 + i.V12 + i.V13 + i.V14 +

i.V15 + i.V16 + i.V17 + i.V18 + i.V19 + i.V20 + i.V21 + i.V22 +

i.V23 + i.V24")

bandit <- OfflineBootstrappedReplayBandit$new(formula = formula, data = top_50_movies)

agents <-

list(Agent$new(ThompsonSamplingPolicy$new(), bandit, "Thompson"),

Agent$new(RandomPolicy$new(), bandit, "Random"),

Agent$new(LinUCBDisjointOptimizedPolicy$new(2.05), bandit, "LinUCB Dis"))

simulation <-

Simulator$new(

agents = agents,

simulations = simulations,

horizon = horizon

)

sim <- simulation$run()

plot(sim,

type = "cumulative",

regret = FALSE,

rate = TRUE,

legend_position = "bottomright")

おわりに

2~3年前に、Tokyo Web Miningの懇親会でContextual Banditの論文いいぞとテラモナギさんが紹介していて、へー、そんなのあるんだと、「へー」の域を出なかったんですが、一歩前進した気がします。先人が切り開いた道を2~3年後に舗装されてから通るというのも遅いなと感じられるので、残業もっと減らして勉強時間増やしたいと思います。

参考情報

バンディット問題の理論とアルゴリズム (機械学習プロフェッショナルシリーズ)
Bandit Algorithms for Website Optimization: Developing, Deploying, and Debugging
Contextual package ~ Japan.R Shota Yasui
Package ‘contextual’
バンディットアルゴリズムの復習３：UCB(Upper Confidence Bound)

カテゴリー: 強化学習

RのContextualパッケージをいじってみた際のメモ書き

はじめに

目次

バンディット問題とは

マーケティング関連でバンディット問題が役に立つ場面

バンディット問題で出てくる数学的な知識と方策

ε-貪欲法

UCB(Upper Confidence Bound)方策

KL-UCB

MED(Minimum Empirical Divergence)方策

トンプソン抽出

Contextual Bandit問題とは

Contextualパッケージでできること

サンプル実行

サンプル1：ABテストによる最適腕選択

ε-貪欲法

ソフトマックスによる方策

UCB方策

サンプル2：文脈付きバンディット問題で映画のレーティングの最適化

サンプル3：文脈付きバンディット問題でMovieLensのTop50の作品における評価の最適化

おわりに

参考情報

多腕バンディットモデルに関する参考文献