はじめに
前回は、連続型確率分布に関するよくある分布とその平均と分散の導出についてひたすら記しました。今回は同じく連続型ながら、正規分布から導かれる確率分布に関して同様に記していこうと思います。大学のときに数理統計学の授業でがっつりやったはずの領域だったのですが、見事に忘れていたので、電車の中などでしっかりと復習していこうと思います。
※PC版でないと数式が切れてしまうので、SP版での閲覧はおすすめしません。私、SKUEのスマホだけは表示崩れがないようにチェックしております。通勤電車で定期的に読むので。
今回登場する連続分布
『数理統計学―基礎から学ぶデータ解析』という本に登場するものを式を補いながら紹介します。
1.カイ二乗分布
ガンマ分布\( \Gamma \left ( \frac{n}{2}, \frac{1}{2} \right ) \)、すなわち、密度関数が以下の式で与えられるとき、この確率分布を自由度nの\( \chi^2 \)分布という。
$$ f(x ; n) = \frac{1}{ 2^{ \frac{n}{2}} \Gamma \left ( \frac{n}{2} \right ) }x^{\frac{n}{2}-1} e^{-\frac{x}{2}} \\
x > 0 \\
n = 1, 2, \dots
$$
\( \chi^2 \)分布の再生性
XとYがカイ二乗分布に従うとして、それらの和がカイ二乗分布になる性質を再生性と呼ぶ。
$$ X \sim \chi^2 (m) \\
Y \sim \chi^2 (n) \\
X + Y \sim \chi^2 (m+n)
$$
以下ではこの再生性に関して証明を行う。
ここで\( z = X + Y \)とする。zの密度関数は、以下で表される。
$$ g(z) = \int_0^z f(x ; m) f(y ; n) dx \\
= \int_0^z f(x ; m) f(z-x ; n) dx \\
= \int_0^z \frac{ x^{\frac{m}{2}-1} e^{-\frac{x}{2}} }{2^{\frac{m}{2}} \Gamma \left ( \frac{m}{2} \right ) } \frac{ (z-x)^{\frac{n}{2}-1} e^{-\frac{z-x}{2}} }{2^{\frac{n}{2}} \Gamma \left ( \frac{n}{2} \right ) } dx
$$
ここで、\( u = \frac{x}{z} \)として、変数変換を行う。( \( \frac{dx}{du} = z \quad , x = zu \) )
$$ = \int_0^1 \frac{ (zu)^{\frac{m}{2}-1} e^{-\frac{zu}{2}} }{2^{\frac{m}{2}} \Gamma \left ( \frac{m}{2} \right ) } \frac{ (z-zu)^{\frac{n}{2}-1} e^{-\frac{z(1-u)}{2}} }{2^{\frac{n}{2}} \Gamma \left ( \frac{n}{2} \right ) } z du $$
$$ = \frac{z^{\frac{m}{2} + \frac{n}{2} -1} e^{-\frac{z}{2}} }{ 2^{\frac{m}{2} + \frac{n}{2} } \Gamma \left ( \frac{m}{2} \right ) \Gamma \left ( \frac{n}{2} \right ) } \int_0^1 u^{\frac{u}{2}-1}(1-u)^{\frac{u}{2}-1}du $$
積分記号以降の部分はベータ分布であるから、
以前記したベータ分布とガンマ関数との関係( \( B(x, y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)} \) )より、
$$ = \frac{ e^{-\frac{z}{2}} z^{\frac{m+n}{2} -1} }{ \Gamma \left ( \frac{m+n}{2} \right ) 2^{\frac{m+n}{2} } } $$
これは\( \chi^2 (m+n) \)の確率密度関数である。
定理:\( X_1, X_2, \dots , X_n \)は独立に正規分布\( N(0, 1) \)に従うとき、\( Y = X_1^2 + X_2^2 + \dots + X_n^2 \)は\( \chi^2(n) \)に従う。
以下はUCLAのレクチャーノートに従っています。
まず、\( X_i^2 \)がカイ二乗分布に従うことを示します。
標準正規分布に従う変数zの二乗としてxを定義します。
$$ x = z^2 \\
f(z) = \frac{1}{\sqrt {2 \pi } } e^{-\frac{1}{2}z^2}
$$
xの確率は以下のように表される。
$$ F_X (x) = P( X \le x ) \\
= P(Z^2 \le x ) \\
= P( – \sqrt {x} \le Z \le \sqrt {x} )
$$
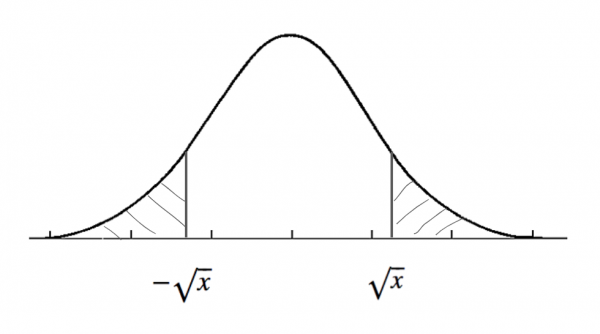
この場合、求めたい確率は1から両端を差し引いたものとなる。
$$ {left} = F_z(-\sqrt {x}) \\
{right} = 1 – F_z(\sqrt {x}) \\
F_X (x) = 1 – {left} – {right} \\
= F_z(\sqrt {x}) – F_z(-\sqrt {x})
$$
確率密度を求めるために両辺をxで微分し整理する。
= \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}x}\frac{1}{2}x^{-\frac{1}{2}} – (-1) \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}x}\frac{1}{2}x^{-\frac{1}{2}} \\\\
= \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}x}x^{-\frac{1}{2}} \\\\
= \frac{x^{-\frac{1}{2}} e^{-\frac{x}{2}}}{2^{\frac{1}{2}} \Gamma \left ( \frac{1}{2} \right ) } \sim \chi_1^2
$$
これは自由度1のカイ二乗分布であり、正規分布に従う変数の二乗は自由度1のカイ二乗分布に従うことが示された。
ここで、ガンマ分布の積率母関数について導出を行う。
$$ M_{X}(t) = E \left ( e^{tX} \right ) \\
= \int _{0}^{\infty} e^{tx} \frac{x^{\alpha – 1} e^{-\frac{x}{\beta}}}{\beta^{\alpha} \Gamma \left ( \alpha \right )} dx \\
= \frac{1}{\beta^{\alpha} \Gamma \left ( \alpha \right )}\int _{0}^{\infty} x^{\alpha – 1} e^{-x \left ( \frac{1-\beta t}{\beta} \right ) }dx
$$
ここで以下の変数変換を行う。
$$ y = x \left ( \frac{1-\beta t}{\beta} \right ) $$
つまり、\( x = \frac{\beta}{1-\beta t} y \)、\( \frac{dx}{dy} = \frac{\beta}{1-\beta t} \)であるから、これらを代入すると、
= \frac{1}{\beta^{\alpha} \Gamma \left ( \alpha \right )} \left ( \frac{\beta}{1-\beta t} \right )^{\alpha – 1} \frac{\beta}{1-\beta t} \int _{0}^{\infty} y^{\alpha – 1}e^{-y} dy
\\\\
= (1-\beta t)^{-\alpha}
$$
よって、先程求めた自由度1のカイ二乗分布は積率母関数で表すと以下のようになる。
$$ M_X(t) = M_{Z^2}(t) = (1-2t)^{-\frac{1}{2}} $$
今回の定理において、\( X_i^2 \)は各々が独立なので、先程求めた自由度1のカイ二乗分布の積率母関数を掛け合わせることで\( Y = \sum_{i}^{n} X_i^2 \)の積率母関数は求まる。
= (1-2t)^{-\frac{1}{2}} \times (1-2t)^{-\frac{1}{2}} \times \dots \times (1-2t)^{-\frac{1}{2}} \\\\
= (1-2t)^{-\frac{n}{2}}
$$
これは自由度nのカイ二乗分布の積率母関数と同じであるから、\( Y = \sum_{i}^{n} X_i^2 \)が自由度nのカイ二乗分布に従うことが示された。
カイ二乗分布の平均
$$ E \left ( X \right ) = \int _{0}^{\infty} x \frac{1}{ 2^{ \frac{n}{2}} \Gamma \left ( \frac{n}{2} \right ) }x^{\frac{n}{2}-1} e^{-\frac{x}{2}}dx \\
= \int _{0}^{\infty} \frac{1}{ 2^{ \frac{n}{2}} \Gamma \left ( \frac{n}{2} \right ) }x^{\frac{n}{2}} e^{-\frac{x}{2}}dx
$$
ここで、部分積分の公式より
= \left [ \frac{2}{n+2}x^{\frac{n}{2}+1} e^{-\frac{x}{2}} \right ]_0^{\infty}- \frac{n}{2}(-2) \int _{0}^{\infty} x^{\frac{n}{2}-1} e^{-\frac{x}{2}}dx
\\\\
= n \int _{0}^{\infty} x^{\frac{n}{2}-1} e^{-\frac{x}{2}}dx
$$
となるから、カイ二乗分布の積分が1になることから、平均は
$$ E \left ( X \right ) = n \int _{0}^{\infty} \frac{1}{ 2^{ \frac{n}{2}} \Gamma \left ( \frac{n}{2} \right ) }x^{\frac{n}{2}-1} e^{-\frac{x}{2}}dx \\
= n
$$
となる。
カイ二乗分布の分散
分散は
$$ V(X) = E \left ( X^2 \right ) – \left [ E(X) \right ]^2 $$
より求まるので、
$$ E(X^2) = \int _{0}^{\infty} x^2 \frac{1}{ 2^{ \frac{n}{2}} \Gamma \left ( \frac{n}{2} \right ) }x^{\frac{n}{2}-1} e^{-\frac{x}{2}}dx \\
= \int _{0}^{\infty} \frac{1}{ 2^{ \frac{n}{2}} \Gamma \left ( \frac{n}{2} \right ) }x^{\frac{n}{2}+1} e^{-\frac{x}{2}}dx
$$
ここで、部分積分の公式より
= \left [ \frac{2}{n+4}x^{\frac{n}{2}+2} e^{-\frac{x}{2}} \right ]_0^{\infty}- \frac{n+2}{2}(-2) \int _{0}^{\infty} x^{\frac{n}{2}} e^{-\frac{x}{2}}dx \\\\
= (n+2)\int _{0}^{\infty} x^{\frac{n}{2}} e^{-\frac{x}{2}}dx \\\\
= (n+2) \left [ \left [ \frac{2}{n+2}x^{\frac{n}{2}+1} e^{-\frac{x}{2}} \right ]_0^{\infty}- \frac{n}{2}(-2) \int _{0}^{\infty} x^{\frac{n}{2}-1} e^{-\frac{x}{2}}dx \right ] \\\\
= n(n+2) \int _{0}^{\infty} x^{\frac{n}{2}-1} e^{-\frac{x}{2}}dx
$$
となるから、カイ二乗分布の積分が1になることから、
= n(n+2)
$$
よってカイ二乗分布の分散は
$$ V(X) = n(n+2) – n^2 \\
= 2n $$
となる。
2.t分布
以下の確率密度関数で与えられる分布をt分布と呼ぶ。
$$ f(x ; n) = \frac{ \Gamma \left ( \frac{n+1}{2} \right ) }{ \sqrt {n \pi} \Gamma \left ( \frac{n}{2} \right ) \left ( 1 + \frac{x^2}{n} \right )^{\frac{n+1}{2}} } \\
-\infty < x < \infty \\
n = 1, 2, \dots
$$
確率密度関数から明らかなように、パラメータは自由度nだけからなる。
なお、自由度が1のとき、t分布はコーシー分布と同じになる。
$$ f(x ; 1) = \frac{1}{\pi} \frac{1}{1 + x^2} $$
t分布の特徴としては、
・y軸に関して対称
・標準正規分布よりも左右に裾が重い
・自由度が1よりも大きいとき、xf(x)は可積分となり、平均は0となる。
・自由度が1の場合はコーシー分布と同じであるため平均も分散も存在しない。
などがあげられる。
定理:Xは\( N(0, 1) \)に、Yは\( \chi^2(n) \)にそれぞれ従い、かつ互いに独立とする。このとき、\( t = \frac{x}{\sqrt {y/n}} \)は\( t(n) \)に従う。
XとYの結合密度関数は
$$ f(x, y) = \frac{1}{\sqrt {2\pi}} e^{ -\frac{x^2}{2}} \frac{ y^{ \frac{n}{2} -1} }{ 2^{ \frac{n}{2} } \Gamma \left ( \frac{n}{2} \right ) } e^{ – \frac{y}{2} } $$
となる。
$$ t = \frac{x}{\sqrt {y / n} } \\
x = t \sqrt {y / n} = t \sqrt {s / n} \\
y = s
$$
とおいて、確率の変数変換を行うと、tとsの結合密度関数は、
$$ g(t, s) = f \left ( t \sqrt {s / n}, s \right ) | J | \\
= f \left ( t \sqrt {s / n}, s \right ) \begin{bmatrix} \frac{\partial x}{\partial t} & \frac{\partial x}{\partial s} \\ \frac{\partial y}{\partial t} & \frac{\partial y}{\partial s} \end{bmatrix} \\
= f \left ( t \sqrt {s / n}, s \right ) \sqrt {s / n} \\
= \frac{1}{\sqrt {2\pi}} e^{ -\frac{t^2 \frac{s}{n} }{2}} \frac{ s^{ \frac{n}{2} -1} }{ 2^{ \frac{n}{2} } \Gamma \left ( \frac{n}{2} \right ) } e^{ – \frac{s}{2} } \sqrt {s / n} \\
= \frac{ s^{ \frac{1}{2}(n-1)} e^{-\frac{1}{2} \left ( 1 + \frac{t^2}{n}s \right ) } }{ \sqrt {2\pi} 2^{ \frac{n}{2} } \Gamma \left ( \frac{n}{2} \right ) \sqrt {n} }
$$
ここで\( u = \frac{1}{2} \left ( 1 + \frac{t^2}{n} \right ) s \)とおく。なお、\( s = \frac{2u}{ \left ( 1 + \frac{t^2}{n} \right ) } \)、\( \frac{ds}{du} = \frac{2}{1 + \frac{t^2}{n}} \)であるからこれらを代入し、分子について定積分をとりtを固定し、sを変換する。
$$ \int _{0}^{\infty} s^{ \frac{1}{2} (n-1)} e^{ – \frac{1}{2} \left ( 1 + \frac{t^2}{n} \right )s }ds \\
= \int _{0}^{\infty} \left ( \frac{2u}{ 1 + \frac{t^2}{n} } \right )^{ \frac{1}{2}(n-1) }e^{-u} \frac{ds}{du}du \\
= \int _{0}^{\infty} \left ( \frac{2u}{ 1 + \frac{t^2}{n} } \right )^{ \frac{1}{2}(n-1) }e^{-u} \frac{2}{1 + \frac{t^2}{n}} du \\
= \frac{ 2^{ \frac{1}{2} (n-1) + 1 } }{ \left ( 1 + \frac{t^2}{n} \right )^{ \frac{1}{2}(n-1) + 1 } } \int _{0}^{\infty} u^{ \frac{1}{2}(n-1)} e^{-u}du \\
= \frac{ 2^{ \frac{1}{2} (n+1) } }{ \left ( 1 + \frac{t^2}{n} \right )^{ \frac{1}{2}(n+1)} } \int _{0}^{\infty} u^{ \frac{1}{2}(n-1)} e^{-u}du
$$
ここで、ガンマ関数の定義より、
$$ \Gamma ( \alpha ) = \int_{0}^{\infty} u^{ \alpha – 1} e^{-u}du \\
\alpha – 1 = \frac{1}{2}(n-1) \\
\alpha = \frac{1}{2}(n+1)
$$
であるから、これを考慮すると、
$$ = \frac{ 2^{ \frac{1}{2} (n+1) } }{ \left ( 1 + \frac{t^2}{n} \right )^{ \frac{1}{2}(n+1)} } \Gamma \left ( \frac{1}{2} (n+1) \right ) $$
となる。
以上より、tの密度関数は
= \frac{ 2^{ \frac{1}{2} (n+1) } }{ \left ( 1 + \frac{t^2}{n} \right )^{ \frac{1}{2}(n+1)} } \Gamma \left ( \frac{1}{2} (n+1) \right ) \frac{1}{\sqrt {2\pi} 2^{ \frac{n}{2} } \Gamma \left ( \frac{n}{2} \right ) \sqrt {n}} \\\\
= \frac{ \Gamma \left ( \frac{n+1}{2} \right ) }{ \sqrt{n \pi} \Gamma \left ( \frac{n}{2} \right ) \left ( 1 + \frac{t^2}{n} \right )^{ \frac{n+1}{2}} }
$$
これはt分布の密度関数と同じである。
t分布の平均
$$ E \left ( X \right ) = \int _{-\infty}^{\infty} x \frac{ \Gamma \left ( \frac{n+1}{2} \right ) }{ \sqrt {n \pi} \Gamma \left ( \frac{n}{2} \right ) \left ( 1 + \frac{x^2}{n} \right )^{\frac{n+1}{2}} } dx $$
奇関数であることから
$$ = 0 $$
となる。
t分布の分散
分散は
$$ V(X) = E \left ( X^2 \right ) – \left [ E(X) \right ]^2 \\
= E \left ( X^2 \right ) $$
より求まる。
= \int _{-\infty}^{0} x^2 \frac{ \Gamma \left ( \frac{n+1}{2} \right ) }{ \sqrt {n \pi} \Gamma \left ( \frac{n}{2} \right ) \left ( 1 + \frac{x^2}{n} \right )^{\frac{n+1}{2}} } dx + \int _{0}^{\infty} x^2 \frac{ \Gamma \left ( \frac{n+1}{2} \right ) }{ \sqrt {n \pi} \Gamma \left ( \frac{n}{2} \right ) \left ( 1 + \frac{x^2}{n} \right )^{\frac{n+1}{2}} } dx
$$
偶関数であることから以下のように表される。
$$ = 2 \int _{0}^{\infty} x^2 \frac{ \Gamma \left ( \frac{n+1}{2} \right ) }{ \sqrt {n \pi} \Gamma \left ( \frac{n}{2} \right ) \left ( 1 + \frac{x^2}{n} \right )^{\frac{n+1}{2}} } dx \\
= 2 \frac{ \Gamma \left ( \frac{n+1}{2} \right ) }{ \sqrt {n \pi} \Gamma \left ( \frac{n}{2} \right )} \int _{0}^{\infty} \frac{x^2}{ \left ( 1 + \frac{x^2}{n} \right )^{\frac{n+1}{2}} }dx
$$
ここで、\( y = \frac{1}{1+\frac{x^2}{n}} \)により変数変換を行う。
なお、\( \left ( 1 + \frac{x^2}{n} \right ) = \frac{1}{y} \)、\( x = \left [ \frac{(1-y)n}{y} \right ] ^{\frac{1}{2}} \)、
\( \frac{dx}{dy} = \frac{ (1-y)^{-\frac{1}{2}} n^{\frac{1}{2}}(-1)y^{-\frac{3}{2}}}{2} \)となる。
= 2\frac{ \Gamma \left ( \frac{n+1}{2} \right ) n^{\frac{3}{2}} }{ \sqrt {n \pi} \Gamma \left ( \frac{n}{2} \right )} \int _{0}^{\infty} \frac{(1-y)^{\frac{1}{2}} y^{\frac{n}{2}-2} }{2}dy
$$
ベータ関数( \( B( \alpha, \beta ) = \int_0^{1} t^{\alpha – 1}(1-t)^{ \beta – 1} dt \) )より、
$$ = \frac{ \Gamma \left ( \frac{n+1}{2} \right ) n^{\frac{3}{2}} }{ \sqrt {n \pi} \Gamma \left ( \frac{n}{2} \right )} B\left ( \frac{n-2}{2}, \frac{3}{2} \right ) $$
ベータ関数とガンマ関数の関係より、
$$ B\left ( \frac{n-2}{2}, \frac{3}{2} \right ) = \frac{ \Gamma \left ( \frac{n-2}{2} \right ) \Gamma \left ( \frac{3}{2} \right ) }{ \Gamma \left ( \frac{n-2}{2} + \frac{3}{2} \right ) } \frac{1}{2} \\
= \frac{ \Gamma \left ( \frac{n-2}{2} \right ) \Gamma \left ( \frac{3}{2} \right ) }{ \Gamma \left ( \frac{n}{2} + \frac{1}{2} \right ) }
$$
よって、
$$ = \frac{ \Gamma \left ( \frac{n+1}{2} \right ) n^{\frac{3}{2}} }{ \sqrt {n \pi} \Gamma \left ( \frac{n}{2} \right )} \frac{ \Gamma \left ( \frac{n-2}{2} \right ) \Gamma \left ( \frac{3}{2} \right ) }{ \Gamma \left ( \frac{n}{2} + \frac{1}{2} \right ) } $$
ガンマ関数は\( \Gamma (n) = (n-1) \Gamma (n-1) \)となることから、\( \Gamma (n+1) = n \Gamma (n) \)あるいは\( \Gamma \left( \frac{n}{2} – 1 \right) = \frac{ \Gamma \left ( \frac{n}{2}
\right ) }{\frac{n}{2} – 1} \)であることを用いると、
$$ = \frac{n^{ \frac{3}{2}} \Gamma \left ( \frac{n}{2} -1 \right ) \Gamma \left ( \frac{n}{2} + 1 \right ) }{ n^{\frac{1}{2}} \sqrt{\pi} \Gamma \left ( \frac{n}{2} \right ) } \\
= \frac{n \Gamma \left ( \frac{n}{2} \right ) }{ \pi^{\frac{1}{2}} \Gamma \left ( \frac{n}{2} \right ) \left ( \frac{n}{2} – 1 \right )} \frac{1}{2} \Gamma \left ( \frac{n}{2} \right ) \\
= \frac{n}{n-2}
$$
となる。
よって、
$$ V(X) = \frac{n}{n-2} $$
3.F分布
以下の確率密度関数で与えられる分布をF分布と呼ぶ。
$$ f(x;m;n) = \frac{ \Gamma \left ( \frac{m+n}{2} \right ) m^{ \frac{m}{2} } n^{ \frac{n}{2} } }{ \Gamma \left ( \frac{m}{2} \right ) \Gamma \left ( \frac{n}{2} \right ) } \frac{ x^{ \frac{m}{2} -1}}{ (mx+n)^{ \frac{m+n}{2} } } \\
x > 0 \\
m, n = 1, 2, \dots
$$
定理:Xは\( \chi^2(m) \)に、Yは\( \chi^2(n) \)に独立に従うとする。このとき、\( F = \frac{ \frac{1}{m}X }{ \frac{1}{n}Y } \)は\( F(m, n) \)に従う。
ここで、\( (X, Y) \rightarrow (F, U) \)と確率の変数変換を行う。
\(
\begin{cases}
F = \frac{ \frac{1}{m}X }{ \frac{1}{n}Y } \\
U = Y \\
\end{cases}
\)
また、\( X = \frac{1}{n}YFM \)、\( Y = U \)となる。
よって確率の変数変換の際のヤコビアンは、
$$ \begin{bmatrix} \frac{\partial X}{\partial F} & \frac{\partial X}{\partial U} \\ \frac{\partial Y}{\partial F} & \frac{\partial Y}{\partial U} \end{bmatrix} = \begin{bmatrix} \frac{1}{n}Um & 0 \\ 0 & 1 \end{bmatrix} = \frac{m}{n}U $$
となる。
FとUの結合分布の密度関数は
$$ h(x, y) = \frac{ x^{ \frac{m}{2} -1} e^{ – \frac{x}{2} }} { 2^{ \frac{m}{2}} \Gamma \left ( \frac{m}{2} \right )} \frac{ y^{ \frac{n}{2} -1} e^{ – \frac{y}{2} }} { 2^{ \frac{n}{2}} \Gamma \left ( \frac{n}{2} \right )} $$
となる。
確率の変数変換を行い整理すると、
$$ g(f,u) = h(x, y) |J | \\
= h \left ( \frac{1}{n}ufm , u \right ) \left | \frac{m}{n}u \right | \\
= \frac{ u^{\frac{m+n}{2} -1} n^{-\frac{m}{2}} m^{\frac{m}{2}} f^{\frac{m}{2} -1} e^{-\frac{u}{2} \left ( \frac{mf}{n} + 1 \right ) } }{ 2^{ \frac{m}{2} } 2^{ \frac{n}{2} } \Gamma \left ( \frac{m}{2} \right ) \Gamma \left ( \frac{n}{2} \right ) }
$$
ここでfを固定して、\( t = \frac{1}{2} \left ( \frac{mf}{n} + 1 \right ) u \)として変数変換を行う。なお、\( u = \frac{2t}{ \frac{mf}{n}+1 } \)、\( \frac{du}{dt} = \frac{2}{ \frac{mf}{n} + 1 } \)となる。
= \frac{ n^{-\frac{m}{2}} m^{\frac{m}{2}} f^{\frac{m}{2} -1} }{ 2^{ \frac{m}{2} } 2^{ \frac{n}{2} } \Gamma \left ( \frac{m}{2} \right ) \Gamma \left ( \frac{n}{2} \right ) } \int_0^{\infty} e^{-\frac{u}{2} \left ( \frac{mf}{n} + 1 \right ) } u^{\frac{m+n}{2} -1} du
$$
ここで積分の中についてのみ注目すると、
= \int_0^{\infty} e^{-t} \frac{2}{ \frac{mf}{n} + 1 } \left ( \frac{2t}{ \frac{mf}{n} + 1} \right )^{ \frac{m+n}{2}-1 }dt \\\\
= \left ( \frac{2n}{mf+n} \right )^{\frac{m+n}{2}} \int_0^{\infty} t^{ \frac{m+n}{2}-1}e^{-t}dt
$$
よって、
ガンマ関数の定義より、
$$ \Gamma ( \alpha ) = \int_{0}^{\infty} u^{ \alpha – 1} e^{-u}du \\
\alpha – 1 = \frac{m+n}{2} – 1 \\
\alpha = \frac{m+n}{2}
$$
であるから、これを考慮し整理する。
= \frac{ \Gamma \left ( \frac{m+n}{2} \right ) m^{ \frac{m}{2} } n^{ \frac{n}{2} } }{ \Gamma \left ( \frac{m}{2} \right ) \Gamma \left ( \frac{n}{2} \right ) } \frac{ f^{ \frac{m}{2} -1}}{ (mf+n)^{ \frac{m+n}{2} } }
$$
これはF分布の確率密度関数である。
F分布の平均
= \int_0^{\infty} \frac{ \Gamma \left ( \frac{m+n}{2} \right ) m^{ \frac{m}{2} } n^{ \frac{n}{2} } }{ \Gamma \left ( \frac{m}{2} \right ) \Gamma \left ( \frac{n}{2} \right ) } \frac{ x^{ \frac{m}{2}}}{ (mx+n)^{ \frac{m+n}{2} } } dx
$$
ここで、\( y = \frac{x}{mx+n} \)と変数変換すると、\( x = \frac{ny}{1-my} \)、\( \frac{dx}{dy} = \frac{n}{(1-my)^2} \)、\( mx + n = \frac{nym}{1-my} + n = \frac{n}{1-my} \)であるから、これらを代入すると、
= \int_0^{\infty} \frac{ \Gamma \left ( \frac{m+n}{2} \right ) m^{ \frac{m}{2} } n^{ \frac{n}{2} } }{ \Gamma \left ( \frac{m}{2} \right ) \Gamma \left ( \frac{n}{2} \right ) } y^{\frac{m+n}{2}} \left ( \frac{ny}{1-my} \right )^{-\frac{n}{2}} \frac{1}{n} \left ( \frac{n}{1-my} \right )^2 dy
$$
ここで、\( z=my \)と変数変換すると、\( y = \frac{z}{m} \)、\( \frac{dy}{dz} = \frac{1}{m} \)であるから、これらを代入すると、
= \frac{ \Gamma \left ( \frac{m+n}{2} \right ) }{ \Gamma \left ( \frac{m}{2} \right ) \Gamma \left ( \frac{n}{2} \right ) }m^{-1}n \int_0^{\infty} z^{ \frac{m}{2}}(1-z)^{\frac{n}{2}-2}dz
$$
ベータ関数、\( B(\alpha , \beta) = \int_0^{1} t^{\alpha – 1}(1-t)^{\beta -1}dt \)の定義より、\( \alpha = \frac{m}{2} + 1 \)、\( \beta = \frac{n}{2} -1 \)であるから、
$$ B \left ( \frac{m}{2}+1, \frac{n}{2} -1 \right ) = \int_0^{\infty} z^{ \frac{m}{2}}(1-z)^{\frac{n}{2}-2}dz $$
ベータ関数とガンマ関数の関係式より、
$$ B \left ( \frac{m}{2}+1, \frac{n}{2} -1 \right ) = \frac{ \Gamma \left ( \frac{m}{2} + 1 \right ) \Gamma \left ( \frac{n}{2} – 1 \right ) }{ \Gamma \left ( \frac{m+n}{2} \right ) } $$
となる。
よって、
$$ E(X) \\
= \frac{ \Gamma \left ( \frac{m+n}{2} \right ) }{ \Gamma \left ( \frac{m}{2} \right ) \Gamma \left ( \frac{n}{2} \right ) }m^{-1}n \frac{ \Gamma \left ( \frac{m}{2} + 1 \right ) \Gamma \left ( \frac{n}{2} – 1 \right ) }{ \Gamma \left ( \frac{m+n}{2} \right ) } \\
= \frac{n}{n-2}
$$
となる。
F分布の分散
分散は
$$ V(X) = E \left ( X^2 \right ) – \left [ E(X) \right ]^2 $$
より求まる。
= \frac{ \Gamma \left ( \frac{m+n}{2} \right ) m^{ \frac{m}{2} } n^{ \frac{n}{2} } }{ \Gamma \left ( \frac{m}{2} \right ) \Gamma \left ( \frac{n}{2} \right ) } \int_0^{\infty} \frac{ x^{ \frac{m}{2} -1}}{ (mx+n)^{ \frac{m+n}{2} } } dx
$$
ここで、先ほどと同様に変数変換を行うが、ここでは積分以降にのみ注目する。
= \int_0^{\infty} \left ( \frac{ny}{1-my} \right )^{ \frac{m}{2}+1 } \left ( \frac{n}{1-my} \right )^{ -\frac{m+n}{2}}\frac{1}{n} \left ( \frac{n}{1-my} \right )^{2} dy \\\\
= \int_0^{\infty} \left ( \frac{ny}{1-my} \right )^{ -\frac{n}{2}+1 } \frac{1}{n} \left ( \frac{n}{1-my} \right )^{2} dy
$$
ここで、\( z = my \)と変数変換を行う。なお、\( y = \frac{z}{m} \)、\( \frac{dy}{dz} = \frac{1}{m} \)であるから、これらを代入すると、
= m^{ -\frac{m}{2} -2 }n^{- \frac{n}{2} + 2} \int_0^{\infty} z^{ \frac{m}{2} +1 }(1-z)^{ \frac{n}{2} -3 }dz
$$
ベータ関数、\( B(\alpha , \beta) = \int_0^{1} t^{\alpha – 1}(1-t)^{\beta -1}dt \)の定義より、\( \alpha = \frac{m}{2} + 2 \)、\( \beta = \frac{n}{2} -2 \)であるから、
よって、
ベータ関数とガンマ関数の関係式より、
$$ B \left ( \frac{m}{2}+2, \frac{n}{2} -2 \right ) = \frac{ \Gamma \left ( \frac{m}{2} + 2 \right ) \Gamma \left ( \frac{n}{2} – 2 \right ) }{ \Gamma \left ( \frac{m+n}{2} \right ) } $$
となる。
よって、
= \frac{n^2}{m^2} \frac{ \Gamma \left ( \frac{m+n}{2} \right ) }{ \Gamma \left ( \frac{m}{2} \right ) \Gamma \left ( \frac{n}{2} \right ) } \frac{ \left ( \frac{m}{2} + 2 \right ) \frac{m}{2} \Gamma \left ( \frac{m}{2} \right ) }{ \Gamma \left ( \frac{m+n}{2} \right ) } \frac{ \Gamma \left ( \frac{n}{2} \right ) }{ \left ( \frac{n}{2} – 2 \right ) \left ( \frac{n}{2} -1 \right ) } \\\\
= \frac{n^2 \left ( \frac{m+2}{2} \right ) \frac{m}{2} }{m^2 \left ( \frac{n-4}{2} \right ) \left ( \frac{n-2}{2} \right ) } \\\\
= \frac{n^2(m+2)}{m(n-4)(n-2)}
$$
分散の式にあてはめると、
$$ V(X) = E \left ( X^2 \right ) – \left [ E(X) \right ]^2 \\
= \frac{n^2(m+2)}{m(n-4)(n-2)} – \frac{n^2}{(n-2)^2} \\
= \frac{2n^2(n+m-2)}{m(n-4)(n-2)^2}
$$
となる。
参考文献
[1] Distributions related to the normal distribution
[2] 鈴木・山田 (1996), 『数理統計学―基礎から学ぶデータ解析』, 内田老鶴圃