A4用紙1枚にまとめるイメージでメモを残そうという取り組みです。
今回はメディアミックスモデリングに関して仕事があった際に参照できるメモの一つとして残します。
先日、Python/STAN Implementation of Multiplicative Marketing Mix Modelに参考文献としてBayesian Methods for Media Mix Modeling with Carryover and Shape Effectsの存在を知りました。時系列の重回帰の一種じゃないかと思っていたんですが、天下のGoogle様がどのようにマーケティングの成果を測ろうとしているのか、この論文から知ってみようと思います。
ちなみに、Python/STAN Implementation of Multiplicative Marketing Mix Modelの写経したものはMarketingMixModelingに残しています。
このコードでマーケティングにおけるチャネルごとのROAS(Return On Advertising Spend)を推定することができます。
以下の図はコードを回すことで得られるものですが、チャネルごとのROASの事後分布となります。
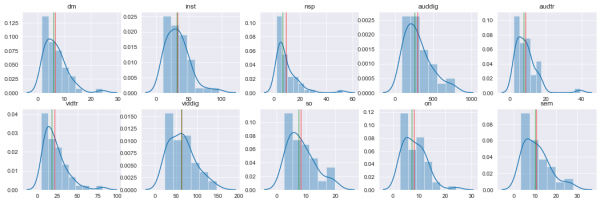
この図もコードを回すことで得られるものですが、広告などの支出に関する売上の関数をフィットしたものになります。精度高くこれらの関数を求めれば、過剰に広告に投資している可能性のあるチャネルを見つけることが可能になります。
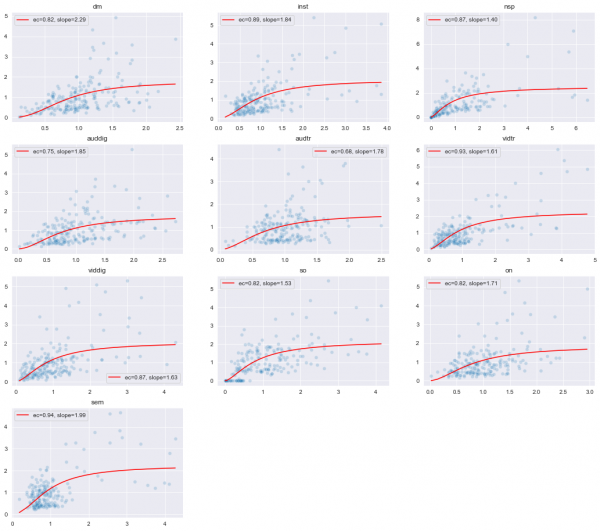
目次
Abstract
Introduction
Model Specification
Estimating the Bayesian Model
Attribution Metrics and Optimal Media Mix
Application to a Simulated Data Set
Impact of Sample Size on Estimation Accuracy
Choice of Priors
Application to Real Data and Model Selection
Conclusion
Abstract
ROASやmROASに関するアトリビューション分析をベイズモデリングで行い、事後分布から効果を推定している。
広告関連のデータが、売上などに対して、数ヶ月後に遅れて効果が現れるキャリーオーバー効果の想定、支出を増やしても効果がなくなる収獲低減の想定などをモデルに置いている。
モデルの識別に関してはBICを評価基準として用いている。
Introduction
- Media mix models(MMM)はメディア支出が売上にどのように影響を与えるのかを理解するために、最適なメディア投資を行うための支出の配分を決めるために使われる。
- 扱うデータとしては売上、物価、プロダクトの分布、様々なメディアの支出、マクロ経済や天候、季節性、競合の情報などの外部要因が含まれる。
- RCTが難しいため、あるいは傾向スコアなどのモデリングもデータが少なく難しいため、回帰分析が行われることが多い。
- 線形回帰だと、広告がサチっている効果(広告が飽和している状態)や収獲低減の効果も表現できない。
- 広告にはキャリーオーバー効果と言って、売上への効果が遅れて現れるという可能性が広く信じられている。
- 事前分布に広告に関する様々なノウハウを反映させることで、データ数に比して推定するパラメータの数が多い分析に向きあう。
Model Specification
- モデル構築には週次データが使われるケースが多い。
- 売上のデータ、メディア支出のデータ、コントロール変数として売上と関係してそうなデータが扱われる。コントロール変数は業界によって異なる。
- キャリーオーバー効果
$$ adstock(x_{t-L+1, m}, \dots, x_{t, m} ; w_{m} ,L) = \frac{\sum_{t=0}^{L-1} w_m(l) x_{t-l, m} }{\sum_{l=0}^{L-1} w_m(l)} $$
\( w_m(l) \)は非負のウェイトでラグ期間の関数になっている。
\( L \)はキャリーオーバー効果の最大期間。
\( x_{t, m} \)はある期間のあるメディアへの支出。
論文ではL=13とされている。
ウェイトの関数について、メディアの売上に対する効果は徐々に減っていくが、効果が遅れて生じることもあるので、効果のピークをずらした表現も扱われている。
ウェイトの関数で最初にピークがくる場合、$$ w_{m}^{g} (l; \alpha_{m}) = \alpha_{m}^{l}, \\ l = 0, \dots, L-1 , \\ 0 < \alpha_m < 1 $$ウェイトの関数で遅れてピークがくる場合、
$$ w_{m}^{d} (l; \alpha_{m}, \theta_m) = \alpha_{m}^{(l – \theta)^2}, \\ l = 0, \dots, L-1 , \\ 0 < \alpha_m < 1 ,\\ 0 \leq \theta_m \leq L -1 $$となる。
\( \alpha_m \)はメディアの効果の、ある期から次の期への維持率。
\( \theta_m \)は遅れてピークが現れる程度に関するパラメータ。 - 形状効果
$$Hill(x_{t,m};\mathcal{K}_m, \mathcal{S}_m) = \frac{1}{1+ \left (
\frac{x_{t, m}}{\mathcal{K}_m} \right )^{- \mathcal{S}_m} }, \\ x_{t, m} \geq 0 $$\( x_{t, m} \)はある期間のあるメディアへの支出。
\( \mathcal{S}_m \)は形状に関するパラメータで傾きに関わるもの。
\( \mathcal{K}_m \)は形状に関するパラメータでサチるポイントに関わるもの。
分子に\( \mathcal{K}_m ^{\mathcal{S}_m} \)を足して引くことで、$$ \beta_{m} Hill_{m} (x_{t, m}) = \beta_{m} – \frac{\mathcal{K}_m^{\mathcal{S}_m}\beta_{m}}{x_{t,m}^{\mathcal{S}_m}+\mathcal{K}_m^{\mathcal{S}_m}} $$に変換できる。
なお、\( \beta_m \)は各メディアの回帰係数となる。これでもって各メディア支出の売上に対する効果を見れる。パラメータの大きさによって様々な形状をとりうる。 - キャリーオーバー効果と形状効果をモデルで一緒に表現する。
シンプルにするためにメディア間のシナジー効果を無視している。$$ y_t = \tau + \sum_{m=1}^{M} \beta_m Hill(x_{t, m }^{*}; \mathcal{K}_m,\mathcal{S}_m) + \sum_{c=1}^{C} \gamma_{c}z_{t, c} + \epsilon_t $$\( y_t \)は売上。
\( x_{t, m }^{*} = adstock(x_{t-L+1, m}, \dots, x_{t, m} ; w_{m}, L) \)は前述の広告支出のキャリーオーバー効果を表現したもの。
\( \tau \)は広告支出によらないベースラインの売上。
\( z_{t,c} \)はコントロール変数。
\( \gamma_c \)はコントロール変数の係数。
\( \epsilon_t \)はホワイトノイズ。
Estimating the Bayesian Model
- 階層ベイズに拡張することもできる。
- ハイパーパラメータはメディアの効果が非負であるとか、割合は0から1だとか色々と事前情報として設定する。
Attribution Metrics and Optimal Media Mix
- 経路ごとのROSAやmROASを計算してメディアの最適化をしたい。
- メディアに投資することでの予測売上と、投資なかった場合の売上の差分でもって成果を測る。
- ROASの定義式
$$ ROAS_{m} = \frac{\sum_{t_{0} \leq t \leq t_{1} + L – 1 } \hat Y_{t}^{m} (x_{t-L+1, m}, \dots, x_{t, m}; \Phi) – \hat Y_{t}^{m} (\tilde{x}_{t-L+1, m}, \dots, \tilde{x}_{t, m}; \Phi) }{\sum_{t_{0} \leq t \leq t_{1}} x_{t, m} } $$
\( \hat{Y} \)は売上の予測。
\( \tilde{x} \)はメディアの支出の変化。 - mROASの定義式
$$ mROAS_{m} = \frac{\sum_{t_{0} \leq t \leq t_{1} + L – 1 } \hat Y_{t}^{m} (\tilde{\tilde{x}}_{t-L+1, m}, \dots, \tilde{\tilde{x}}_{t, m}; \Phi) – \hat Y_{t}^{m} (x_{t-L+1, m}, \dots, x_{t, m}; \Phi) }{ 0.01 \times \sum_{t_{0} \leq t \leq t_{1}} x_{t, m} } $$
\( \hat{Y} \)は売上の予測。
\( \tilde{\tilde{x}} \)はメディアの支出の1%の変化。 - ROASの分布は事後分布と上述の定義式から得られる。
- メディアミックスの最適化
予算という制約付きの極値問題を解く。ラグランジュ未定乗数法を用いる。
Application to a Simulated Data Set
- シミュレーションしたデータを使っている。2年間の週次のデータで、売上、3つのメディア、一つのコントロール変数からなる。
Impact of Sample Size on Estimation Accuracy
- 単一のデータセットのみで評価することが難しいので、それぞれが独立した500個のデータセットを生成し、それぞれ推定をしている。
Choice of Priors
- サンプルサイズが小さい場合、事後分布が事前分布の影響を大きく受けるため、事前分布に関して色々と考察している。
- \( \beta \)に関する事前分布。設定次第で結構変わる。メディアの支出にかかってくるので分析に与える影響は大きい。
- \( \mathcal{K}_m \)に関する事前分布。要はサチるポイントに関するもの。設定次第でグラフの挙動が結構変わる。
Application to Real Data and Model Selection
- シャンプーの広告主の実際のデータを使って分析。
- 2.5年の週次データで、反応変数として売上、メディアデータとしてTV・雑誌・ディスプレイ・YouTube・検索、コントロール変数として小売のデータ(平均オンスあたり価格)・重み付けされた全商品の流通量や広告量が扱われている。
- BICを頼りにモデルを選択した。BICは事後分布のデータから計算できる。
Conclusion
- メディアミックスモデルはモデルの識別によって結果が大きく変わる。
- ベイズモデルでキャリーオーバー効果や形状効果を考慮したモデルを求め、それらの事後分布からROASやmROASを計算した。
- データ数が少ないとバイアスの伴った推定となる。事前情報の選定にも慎重になるべき。
- BICでモデルを識別した結果、キャリーオーバー効果や形状効果を想定した設定が選ばれた。
- 残差に自己相関があったため、今回のモデルはまだ不完全で改善の余地がある。