ディリクレNBDモデルのマーケティング分野での適用に関して色々調べてみた

どの企業のマーケティング担当者も、自分が属する市場や自分の会社の商品の需要予測ないし購買行動の予測に関心があると思います。それらを予測できる手法として、ディリクレNBDモデルが候補にあがると思います。
以前、『確率思考の戦略論 USJでも実証された数学マーケティングの力』を読んだ際に、需要のシミュレーションにディリクレNBDモデルが使えるということを知りましたが、繰り返し利用するサービスや消費財向けのアプローチなのかなと思って、自分が扱うサービスへの適用可能性の低さから距離を置いてきました。
ところが、文献によると様々な分野でディリクレNBDモデルを使って生命保険やクレジットカードなどのサービス市場需要の予測がうまくいっているケースがあるらしく、真剣に向き合ってみようと思い調べてみることにしました。

歴史

マーケティングの分野では、消費者の繰り返し購買行動やダブルジョパディの法則など様々な現象を説明するための研究と実践がなされてきました。
そのために確率的なモデルが色々と適用されていきました。

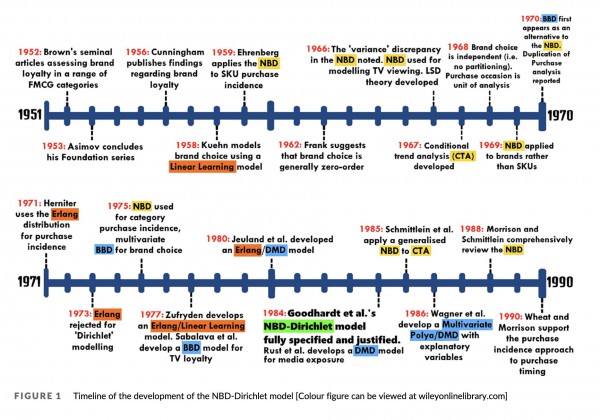
“The Dirichlet model in marketing”という論文の図を引用しますが、1952年ごろからブランドロイヤルティーの研究が始まり、1958年には線形モデルが用いられ、1959年にはNBD(Negative Binomial Distribution：負の二項分布)を用いた購買予測などがなされるようになりました。
それらのアプローチを様々な対象に適用しつつ、1975年にはBBD(Beta Binomial Distribution：ベータ二項分布)が、ついに1984年にはNBD-DirichletモデルがGoodhardtらによって考案されるに至りました。

理論の概要

本家の論文（The Dirichlet: A Comprehensive Model of Buying Behaviour）や“Calculation of Theoretical Brand Performance Measures from the Parameters of the Dirichlet Model”を読まれることをお勧めしますが、この理論が想定しているものは以下の通りです。

・各々の消費者がポワソン過程に従って、負の二項分布に従い購買行動をする。
・消費者ごとの購買率はガンマ分布に従う。
・消費者の利用可能なブランドの選択は多項分布に従う。
・ブランドの選択確率自体は様々な消費者ごとに、多変量ベータ分布、あるいはディリクレ分布に従う。

なお、ディリクレモデルは負の二項分布とディリクレ多変量分布の二つの確率密度関数の結合からなり、二つの分布はそれぞれ独立であることを想定しています。
マーケットにおける購買自体の行動をつかさどる分布（負の二項分布）と、何を選ぶかをつかさどる分布（ディリクレ多変量分布）が独立しているということになります。

まず、負の二項分布についてですが、確率密度関数は以下の通りとなります。
$$ f_{\gamma, \beta}(k) = \frac{\Gamma (\gamma + k)}{\Gamma(\gamma)k!}\frac{\beta^k}{(1+\beta)^{\gamma + k}} \\ \textrm{ for } k = 0, 1, 2,…$$

負の二項分布は二つのパラメータを持ちます。
・形状（shape）パラメータ（$\gamma$）
・尺度（scale）パラメータ（$\beta$）

続いて、ディリクレ多変量分布ですが、確率密度関数は以下の通りとなります。

$$ f_{\alpha_1, \alpha_2, \dots, \alpha_h}(r_1, r_2, \dots, r_h | r_1 + r_2 + \dots + r_h = k ) \\
\frac{\Gamma \left ( \sum_{j=1}^{h} \alpha_j \right ) k! }{ \Gamma \left ( \sum_{j=1}^{h} \alpha_j + k \right ) } \prod_{j=1}^{h} \frac{\Gamma \left ( \alpha_j + r_j \right ) }{r_j! \Gamma \left ( \alpha_j \right )}$$

$r_h$などはそのマーケットにおける特定ブランドの購買率で、ブランド数がhだけあるとしています。
なお、
$$ r_1 + r_2 + \dots + r_h = k $$
で、足し合わせるとkがマーケット自体の購買率になるようになっています。ディリクレ多変量分布はブランドの数だけ、h個の正のパラメータ$ \alpha_1,\alpha_2, \dots, \alpha_h $を持ちます。

ディリクレモデルは、以上の負の二項分布とディリクレ多変量分布を結合したもので、確率密度関数は以下の通りになります。

$$ f_{\gamma, \beta, \alpha_1, \alpha_2, \dots, \alpha_h}(r_1, r_2, \dots, r_h ) = \\ f_{\gamma, \beta}(k) f_{\alpha_1, \alpha_2, \dots, \alpha_h}(r_1, r_2, \dots, r_h | r_1 + r_2 + \dots + r_h = k )$$

この確率密度関数に色々かけて期待値を計算することで以下のようなものを算出することができます。
・あるブランドの購買者ごとの、あるブランドの購買の数の理論値
・プロダクトクラスでの購買の数の平均値
・あるブランドのみを買う母集団の割合
・購買者の平均購買頻度

諸々の式の導出は「[確率思考の戦略論] 1.確率理論の導入とプレファレンスの数学的説明」に詳しく書かれているので、見てみることをお勧めします。
数理統計学の知識とか、ベータ関数・ガンマ関数などの知識があれば式変形などに関してスムーズに理解できると思います。

ただ、この手法自体への批判などもないわけではなく、先ほどあげた論文、“The Dirichlet model in marketing”では、消費者行動を理解するのにつながるモデルではないとか、意思決定を扱っているモデルではないとする批判などがあるようです。ただ、幅広いマーケットで予測されてきた実績もあることから、モデルの限界を知りつつ適用するマーケットを増やしていくことが実務家に求められているのかなと思われます。

適用例

ディリクレモデルが様々な市場で適用されている事例が、『ディリクレモデルの境界条件 ― サービスへの適用可能性と限界 ―』という論文に記されていました。

当初は、インスタントコーヒー市場、衣料用洗剤市場、シャンプー市場などの最寄品（計画的に購入されることが少なく、単価は低く、何度も繰り返し購入される製品・サービス）のみで近似できるとされていましたが、
近年では銀行市場、クレジットカード市場、ガソリンスタンド市場、スーパーマーケット市場、テレビ番組市場、ファーストフード市場、オーケストラ市場、フットボールリーグ市場、野球市場などのサービス業や、スポーツウェアや自動車などの比較的高額な市場においても近似できるとされています。

データについて

ディリクレモデルの理論値を計算するには、4つのデータが必要とされています。
・1.そのカテゴリを購買した人々の全体に占める割合
・2.カテゴリに占める、いずれかの製品を購買した人々に対して記録された当該製品カテゴリの購買回数の平均
・3.各ブランドを一度でも購入した人々の割合
・4.各ブランドを購買した人々による各ブランドの購買回数の平均値

これらのデータはアンケートなどで収集する必要があるため、ディリクレモデルは総じて時間もお金もかかる手法であると言うこともできると思います。先ほどあげた、『ディリクレモデルの境界条件 ― サービスへの適用可能性と限界 ―』にはWEB調査でどんなアンケートを集めるのかの詳細まで書かれているので、自社の属するマーケットでこのモデルを適用する際は、それらを参考にすると良いと思います。

実践するコード

コードに関しては、こちらのColab（2_nb.ipynb）を書かれている方がおられたので、それを試すのも良いと思います。

ライブラリに関して、2016年と決して新しくないですが、R言語ではNBDdirichletというライブラリがあります。手法が1984年のものですから別に問題はないと思います。

# install.packages("NBDdirichlet")

library(NBDdirichlet)

cat.pen <- 0.56 # 市場浸透度
cat.buyrate <- 2.6 # 購買頻度
brand.share <- c(0.25, 0.19, 0.1, 0.1, 0.09, 0.08, 0.03, 0.02) # ブランドのマーケットシェア
brand.pen.obs <- c(0.2,0.17,0.09,0.08,0.08,0.07,0.03,0.02) # ブランド浸透度
brand.name <- c("Colgate DC", "Macleans","Close Up","Signal","ultrabrite",
                "Gibbs SR","Boots Priv. Label","Sainsbury Priv. Lab.") # ブランド名

dobj <- dirichlet(cat.pen, cat.buyrate, brand.share, brand.pen.obs, brand.name)
print(dobj)
summary(dobj)

# install.packages("NBDdirichlet")

library(NBDdirichlet)

cat.pen <- 0.56 # 市場浸透度

cat.buyrate <- 2.6 # 購買頻度

brand.share <- c(0.25, 0.19, 0.1, 0.1, 0.09, 0.08, 0.03, 0.02) # ブランドのマーケットシェア

brand.pen.obs <- c(0.2,0.17,0.09,0.08,0.08,0.07,0.03,0.02) # ブランド浸透度

brand.name <- c("Colgate DC", "Macleans","Close Up","Signal","ultrabrite",

"Gibbs SR","Boots Priv. Label","Sainsbury Priv. Lab.") # ブランド名

dobj <- dirichlet(cat.pen, cat.buyrate, brand.share, brand.pen.obs, brand.name)

print(dobj)

summary(dobj)

こちらを実行した結果は、以下の通りです。

> print(dobj)
Number of Brands in the Category = 8 
Brand List : Colgate DC : Macleans : Close Up : Signal : ultrabrite : Gibbs SR : Boots Priv. Label : Sainsbury Priv. Lab.
Brands' Market Shares: 0.25 0.19 0.1 0.1 0.09 0.08 0.03 0.02 
Brands' Penetration:   0.2 0.17 0.09 0.08 0.08 0.07 0.03 0.02 
Multiple of Base Time Period: 1 , Current M = 1.456 

Category Penetration = 0.56 , with Buying Rate = 2.6 
Estimated Dirichlet Model Parameters:
NBD: M = 1.46 ,  K = 0.78 ;  Dirichlet: S = 1.3

> print(dobj)

Number of Brands in the Category = 8

Brand List : Colgate DC : Macleans : Close Up : Signal : ultrabrite : Gibbs SR : Boots Priv. Label : Sainsbury Priv. Lab.

Brands' Market Shares: 0.25 0.19 0.1 0.1 0.09 0.08 0.03 0.02

Brands' Penetration: 0.2 0.17 0.09 0.08 0.08 0.07 0.03 0.02

Multiple of Base Time Period: 1 , Current M = 1.456

Category Penetration = 0.56 , with Buying Rate = 2.6

Estimated Dirichlet Model Parameters:

NBD: M = 1.46 , K = 0.78 ; Dirichlet: S = 1.3

このdirichlet関数を使うことで、データを与えるだけで、ディリクレモデルのパラメータMやKやSが簡単に求まりました。

summaryで推定した諸々の値を確認できます。引数で色々と調整するので、実際に使う際はリファレンス（Package ‘NBDdirichlet’）を見てください。頻度のカットオフ値やヘビーユーザーの域値や、ブランド重複を見る際の基準ブランドなどを指定できます。

・buy：理論的なブランド浸透度、購買率、そのブランドの買い手によるマーケット内での購買率
・freq：そのブランドの購買の数の分布（以下の場合、6以上はまとめられている）
・heavy：特定の頻度の買い手におけるマーケットでの理論的なブランド浸透度、購買率
・dup：特定のブランドの購買者が他のブランドも購買している割合

> summary(dobj)
$buy
                     pen.brand pur.brand pur.cat
Colgate DC                0.20      1.82    3.16
Macleans                  0.16      1.76    3.22
Close Up                  0.09      1.68    3.30
Signal                    0.09      1.68    3.30
ultrabrite                0.08      1.67    3.31
Gibbs SR                  0.07      1.66    3.32
Boots Priv. Label         0.03      1.62    3.37
Sainsbury Priv. Lab.      0.02      1.61    3.38

$freq
                        0    1    2    3    4 5   6+
Colgate DC           0.80 0.12 0.04 0.02 0.01 0 0.01
Macleans             0.84 0.10 0.03 0.01 0.01 0 0.00
Close Up             0.91 0.06 0.02 0.01 0.00 0 0.00
Signal               0.91 0.06 0.02 0.01 0.00 0 0.00
ultrabrite           0.92 0.05 0.02 0.01 0.00 0 0.00
Gibbs SR             0.93 0.05 0.01 0.01 0.00 0 0.00
Boots Priv. Label    0.97 0.02 0.01 0.00 0.00 0 0.00
Sainsbury Priv. Lab. 0.98 0.01 0.00 0.00 0.00 0 0.00

$heavy
                     Penetration Avg Purchase Freq
Colgate DC                  0.34              1.61
Macleans                    0.27              1.57
Close Up                    0.15              1.51
Signal                      0.15              1.51
ultrabrite                  0.13              1.50
Gibbs SR                    0.12              1.49
Boots Priv. Label           0.05              1.46
Sainsbury Priv. Lab.        0.03              1.45

$dup
          Colgate DC             Macleans             Close Up               Signal 
                1.00                 0.19                 0.10                 0.10 
          ultrabrite             Gibbs SR    Boots Priv. Label Sainsbury Priv. Lab. 
                0.09                 0.08                 0.03                 0.02

> summary(dobj)

$buy

pen.brand pur.brand pur.cat

Colgate DC 0.20 1.82 3.16

Macleans 0.16 1.76 3.22

Close Up 0.09 1.68 3.30

Signal 0.09 1.68 3.30

ultrabrite 0.08 1.67 3.31

Gibbs SR 0.07 1.66 3.32

Boots Priv. Label 0.03 1.62 3.37

Sainsbury Priv. Lab. 0.02 1.61 3.38

$freq

0 1 2 3 4 5 6+

Colgate DC 0.80 0.12 0.04 0.02 0.01 0 0.01

Macleans 0.84 0.10 0.03 0.01 0.01 0 0.00

Close Up 0.91 0.06 0.02 0.01 0.00 0 0.00

Signal 0.91 0.06 0.02 0.01 0.00 0 0.00

ultrabrite 0.92 0.05 0.02 0.01 0.00 0 0.00

Gibbs SR 0.93 0.05 0.01 0.01 0.00 0 0.00

Boots Priv. Label 0.97 0.02 0.01 0.00 0.00 0 0.00

Sainsbury Priv. Lab. 0.98 0.01 0.00 0.00 0.00 0 0.00

$heavy

Penetration Avg Purchase Freq

Colgate DC 0.34 1.61

Macleans 0.27 1.57

Close Up 0.15 1.51

Signal 0.15 1.51

ultrabrite 0.13 1.50

Gibbs SR 0.12 1.49

Boots Priv. Label 0.05 1.46

Sainsbury Priv. Lab. 0.03 1.45

$dup

Colgate DC Macleans Close Up Signal

1.00 0.19 0.10 0.10

ultrabrite Gibbs SR Boots Priv. Label Sainsbury Priv. Lab.

0.09 0.08 0.03 0.02

この推定結果を使って、売上がどれくらいになるかが高精度にわかるのであれば、ブランドの浸透度が上がるような施策を打つことで、あるいは競合がそれらを打つことで売上がどう変わっていくかをシミュレーションすることもできるかもしれません。
その背景にはダブルジョパディの法則などがあると思うと結構面白そうですね。

参考文献

・The Dirichlet: A Comprehensive Model of Buying Behaviour
・Calculation of Theoretical Brand Performance Measures from the Parameters of the Dirichlet Model
・The Dirichlet model in marketing
・NBDdirichlet-package: NBD-Dirichlet model of consumer buying behavior
・Package ‘NBDdirichlet’
・ディリクレモデルの境界条件 ― サービスへの適用可能性と限界 ―
・[確率思考の戦略論] 1.確率理論の導入とプレファレンスの数学的説明
・Negative Binomial distribution
・Dirichlet distribution

ディリクレNBDモデルのマーケティング分野での適用に関して色々調べてみた

目次

歴史

理論の概要

適用例

データについて

実践するコード

参考文献

コメントを残すコメントをキャンセル

目次

歴史

理論の概要

適用例

データについて

実践するコード

参考文献

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル