はじめに
今回は、rstanarmというパッケージを用いて赤ワインデータを色々といじってみようと思います。
マーケティングの意思決定のための分析などでベイズ統計を使う場面が多々あるのですが、似たような属性のデータがあるのであれば、
一つ一つstanコードを書くのではなく、Rの関数でサクッと実行して試行錯誤していくという形に持っていけたらいいなぁと感じていました。
本気を出すところではstanを、ルーティンワーク的なタスクではrstanarmをみたいな形で使い分けれると良いのではないでしょうか。
rstanarmとは
バックエンドの計算をStanに実行させて、統計モデルの推定を行うためのパッケージ。R上でlm関数のように簡単にベイズ推定を行うことができる。対象ユーザーはベイズ推定に慣れ親しんでいない頻度主義系のソフトウェアユーザー。
詳しくはこちら。
インストールする
まずはrstanarmのインストールするのですが、コケまくりました。そのため、バージョンを下げてみることにします。
|
1 |
devtools::install_version("rstanarm", version = "2.17.3", repos = "http://cran.us.r-project.org") |
ここに過去のバージョンがありますが、2.17.4だと動かなかったものの、2.17.3なら動きました。
rstanarmのサンプルを回してみる
今回は、以下の文献を参考にして、大人のIrisとも言える、ワインデータを扱い、質の高いワインかどうかを決める要素を探ります。
How to Use the rstanarm Package | Jonah Gabry and Ben Goodrich
こちらの文献には、ベイズ分析の4つのステップとして以下があげられています。
- 1.同時分布の特定(同時分布は事前分布と条件付きの尤度をかけ合わせたもの。)
- 2.MCMCで事後分布を描く
- 3.モデルがフィットしているか評価する
- 4.事後予測分布を描き、結果に影響を与える予測項を確認する。
これらのステップをできるだけ素早くできると良いですね。
まずはデータを読み込んで、スケーリングしておきます。(可視化結果は前回と同じなので、載せません。)
加えて、6点以上の評価であれば1を取る二項変数を作成しておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
library(tidyverse) library(GGally) library(rstanarm) library(shinystan) library(loo) wine_dataset <- read.csv("http://ieor.berkeley.edu/~ieor265/homeworks/winequality-red.csv", sep=";" ) #可視化 wine_dataset_vis <- wine_dataset ggpairs(wine_dataset_vis) wine_dataset <- wine_dataset %>% mutate( y = if_else(condition = quality > 6, 1, 0 )) wine_dataset <- wine_dataset %>% mutate_at(funs(scale(.)), .vars = c(1:11)) wine_dataset <- wine_dataset %>% select(-quality) |
GLMでロジスティックモデルを推定し、rstanarmで推定した結果と比較します。rstanarmでは傾きや切片の事前分布にスチューデントのt分布を、尤度にロジスティック分布を設定しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# GLM Estimation ---------------------------------------------------------- wine_glm_1 <- glm(y ~ fixed.acidity + volatile.acidity + citric.acid + residual.sugar + chlorides + free.sulfur.dioxide + total.sulfur.dioxide + density + pH + sulphates + alcohol, data = wine_dataset, family = binomial(link = "logit")) # Bayesian Estimation with rstanarm --------------------------------------- wine_bglm_1 <- stan_glm(y ~ fixed.acidity + volatile.acidity + citric.acid + residual.sugar + chlorides + free.sulfur.dioxide + total.sulfur.dioxide + density + pH + sulphates + alcohol, data = wine_dataset, family = binomial(link = "logit"), prior = student_t(df = 7), prior_intercept = student_t(df = 7), chains = 4, cores = 4, seed = 123) #glmの結果との確認 cbind("model_glm" = coef(wine_glm_1), "model_bayesianglm" = coef(wine_bglm_1 )) model_glm model_bayesianglm (Intercept) -2.81452789 -2.85848089 fixed.acidity 0.47871946 0.48115910 volatile.acidity -0.46215347 -0.46939630 citric.acid 0.11060698 0.10547044 residual.sugar 0.33762729 0.32948671 chlorides -0.41494490 -0.43932815 free.sulfur.dioxide 0.11318519 0.11910296 total.sulfur.dioxide -0.54377987 -0.56297397 density -0.48655012 -0.47686448 pH 0.03461116 0.03067029 sulphates 0.63563064 0.64074793 alcohol 0.80280901 0.82144931 |
ほとんど係数の大きさが同じであることが確認できます。
ベイズ推定の良いところは事後分布から関心のある係数に関しての取りうる値などをシミュレーションできるところですが、
posterior_interval関数で簡単に計算することができます。
|
1 2 3 4 5 6 |
> round(posterior_interval(wine_bglm_1, prob = 0.95, pars = "fixed.acidity"), 2) 2.5% 97.5% fixed.acidity 0.03 0.9 > round(posterior_interval(wine_bglm_1, prob = 0.95, pars = "volatile.acidity"), 2) 2.5% 97.5% volatile.acidity -0.76 -0.2 |
肝心のMCMCの収束診断ですが、shinystanを使います。
やや余談ですが、他のデータセットでshinystanを用いた際に、予測結果にNAsが含まれている場合に、
shinystanが起動しないという問題があり、以下のようなエラー文が吐かれます。
|
1 |
Error in validate_y(y) : NAs not allowed in 'y'. |
調べたところ、こちらのgithubにあるように、
|
1 |
launch_shinystan(womensrole_bglm_1,ppd=FALSE) |
のように引数でppd=FALSEのように設定することで、立ち上げることができました。
3つの基準をクリアしているため、収束しています。
rstanarmの良い点の一つとして、モデルのアップデートが容易に行える点があげられると思いますが、実際、以下のように先程のモデルに変数を追加して推定することができます。
今回は、alcoholを二乗したものを新しい変数として加えます。
|
1 2 |
#モデルのアップデート (wine_bglm_2 <- update(wine_bglm_1, formula. = . ~ . + I(alcohol^2))) |
次に、looパッケージを用いて、更新したモデルと元のモデルの性能の比較を行います。
looパッケージは統計モデルの予測精度の指標として扱われる、WAIC(Widely Applicable Information Criterion)を計算するためのパッケージで、WICは事後分布から得られる対数尤度の平均や分散からなる値として表されます。looはleave-one-out cross-validationのleave-one-outの頭文字。
さっそく入れようと思ったところ、
|
1 |
Error: is.data.frame(data) || is.matrix(data) is not TRUE |
というエラーが出ました。
こちらでも議論されていましたが、
|
1 2 |
remove.packages("loo") devtools::install_github("stan-dev/loo", ref = "v1.1.0") |
でバージョンを2.0.0から1.1.0に落としたら動きました。
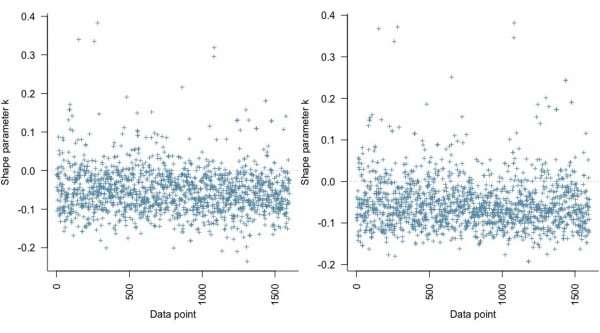
ここで、事後分布が特定のサンプルデータに対して敏感であるかどうかをlooパッケージを用いて可視化します。
|
1 2 3 4 5 6 |
loo_bglm_1 <- loo(wine_bglm_1) loo_bglm_2 <- loo(wine_bglm_2) par(mfrow = 1:2, mar = c(5,3.8,1,0) + 0.1, las = 3) plot(loo_bglm_1, label_points = TRUE) plot(loo_bglm_2, label_points = TRUE) |
縦軸のshape parameter kは推定の信頼性の指標とされ、大きければ大きいほど信頼できないと見なし、横軸は今回推定したワインデータのデータの番号で、左が元のモデル、右が変数を追加したモデルのものです。
どうやらどちらも0.4未満のkに収まっているようです。参考情報の事例では0.5を超えていましたが、moderate outliersと説明されていたので、今回の推定は問題ないと思われます。
続いてモデルの比較を行います。
|
1 2 3 4 |
> #モデルの比較 > compare_models(loo_bglm_1, loo_bglm_2) elpd_diff se 5.4 2.8 |
elpd_diffに関しては右のモデルの精度が高ければ正の値を、低ければ負の値を取るようになっています。標準誤差も返されます。
どうやら変数を追加したモデルの方が、ちょっとだけ良さそうです。
続いて、事後予測分布から、どの変数がどのように予測に影響を与えるのかを確かめます。
比較のためにデータを2つほど作成し、両者において一つだけ変数が違うという状況下での、予測される確率の比較を行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
#パラメータを比較して変数が与える影響を確認する。 newdata <- data.frame(fixed.acidity = c(8.319637,8.319637) , volatile.acidity = c(0.5278205,0.5278205) , citric.acid = c(0.2709756,0.2709756), residual.sugar = c(2.538806,2.538806), chlorides = c(0.08746654,0.08746654) , free.sulfur.dioxide = c(15.87492,15.87492), total.sulfur.dioxide = c(46.46779,46.46779), density = c(0.9967467,0.9967467), pH = c(3.311113,3.311113), sulphates = c(0.6581488,0.6581488), alcohol = c(15.42298,14.42298), 'I(alcohol^2)' = c(15.42298^2,14.42298^2) ) y_rep <- posterior_predict(wine_bglm_2, newdata) summary(y_rep) summary(apply(y_rep, 1, diff)) > summary(y_rep) 1 2 Min. :0.0000 Min. :0.0000 1st Qu.:0.0000 1st Qu.:0.0000 Median :0.0000 Median :0.0000 Mean :0.2402 Mean :0.2717 3rd Qu.:0.0000 3rd Qu.:1.0000 Max. :1.0000 Max. :1.0000 > > summary(apply(y_rep, 1, diff)) Min. 1st Qu. Median Mean 3rd Qu. Max. -1.0000 0.0000 0.0000 0.0315 0.0000 1.0000 |
他の要素をある一定水準で保った際に、alcoholだけ1度下げることで、平均3%ほど高い評価が得られる確率が高まるという考察となります。
以上で、rstanarmの一連の使い方となるのですが、
一部の関数においては、階層ベイズモデルも行えるので、試してみようと思います。
ただ、階層ベイズにするにも、赤ワインのデータしかないので、グループ変数をどうにか作らないといけません。
あまりやりたくはありませんが、データがないので、説明変数を元にk-means(K=3)によるクラスタリングを行い、それをグループ変数とします。
stan_glmer関数を使えば、以下のような簡単な記述で定数項や係数がグループごとに異なるパラメータの分布に従うとする階層ベイズモデルを推定できます。
|
1 2 3 4 5 6 |
stan_glmer(非説明変数 ~ 変数 + ( 変数 - 1 | グループ変数 ), data = wine_dataset_hc, family = binomial(link = "logit"), prior = student_t(df = 7), prior_intercept = student_t(df = 7), chains = 4,cores = 4, seed = 123,iter = 500) |
今回は、切片だけがグループごとに異なるモデル、傾きだけがグループごとに異なるモデル、切片も傾きも異なるモデルを作成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
# Hierachical_Models ------------------------------------------------------ wine_dataset_hc <- wine_dataset wine_dataset_hc$wine_cluster <- as.numeric(kmeans(wine_dataset_hc %>% select(1:11) ,3)$cluster) wine_dataset_hc %>% group_by(wine_cluster) %>% summarize(mean(as.numeric(y)),n()) # Hierarchical Models(Varying Intercept) ------------------------------------------------------- wine_bglm_3 <- stan_glmer(y ~ fixed.acidity + volatile.acidity + citric.acid + residual.sugar + chlorides + free.sulfur.dioxide + total.sulfur.dioxide + density + pH + sulphates + alcohol + ( 1 | wine_cluster ), data = wine_dataset_hc, family = binomial(link = "logit"), prior = student_t(df = 7), prior_intercept = student_t(df = 7), chains = 4,cores = 4, seed = 123,iter = 500) coef(wine_bglm_3) # Hierarchical Models(Varying Slope) --------------------------------------------------------- wine_bglm_4 <- stan_glmer(y ~ fixed.acidity + volatile.acidity + citric.acid + residual.sugar + chlorides + free.sulfur.dioxide + total.sulfur.dioxide + density + pH + sulphates + alcohol + ( fixed.acidity + volatile.acidity + citric.acid + residual.sugar + chlorides + free.sulfur.dioxide + total.sulfur.dioxide + density + pH + sulphates + alcohol - 1 | wine_cluster ), data = wine_dataset_hc, family = binomial(link = "logit"), prior = student_t(df = 7), prior_intercept = student_t(df = 7), chains = 4,cores = 4, seed = 123,iter = 500) coef(wine_bglm_4) # Hierarchical Models(Varying Intercept and Slope) ------------------------------------------- wine_bglm_5 <- stan_glmer(y ~ fixed.acidity + volatile.acidity + citric.acid + residual.sugar + chlorides + free.sulfur.dioxide + total.sulfur.dioxide + density + pH + sulphates + alcohol + ( fixed.acidity + volatile.acidity + citric.acid + residual.sugar + chlorides + free.sulfur.dioxide + total.sulfur.dioxide + density + pH + sulphates + alcohol | wine_cluster ), data = wine_dataset_hc, family = binomial(link = "logit"), prior = student_t(df = 7), prior_intercept = student_t(df = 7), chains = 4,cores = 4, seed = 123,iter = 500) coef(wine_bglm_5) loo_bglm_1 <- loo(wine_bglm_1) loo_bglm_3 <- loo(wine_bglm_3) loo_bglm_4 <- loo(wine_bglm_4) loo_bglm_5 <- loo(wine_bglm_5) |
先程紹介した、looパッケージを使って、ベースとなるモデルとの比較を行います。
|
1 2 3 4 5 6 7 8 9 10 |
> #モデルの比較 > compare_models(loo_bglm_1, loo_bglm_3) elpd_diff se -0.8 0.5 > compare_models(loo_bglm_1, loo_bglm_4) elpd_diff se 1.2 2.5 > compare_models(loo_bglm_1, loo_bglm_5) elpd_diff se 1.0 2.5 |
うーん、残念ながらどのモデルもベースモデルよりも圧倒的に強いものは無さそうです。
感想
まだまだrstanarmの関数やら機能やら定義を全て把握しきれていないですが、そこらへんがクリアーになれば、これまでのstanでの推定業務において生産性が高まる可能性を感じました。
簡単な階層ベイズモデルくらいなら、非常に直感的に書ける点や、変数の追加によるモデルのアップデートが容易な点などはポイント高いなぁと思います。
とはいえ、実務としてマニュアルでstanコードを作成していくのは必須なので、このパッケージを使うことによって、stanコードの改善に時間をより一層割けるようになるなら、それが一番だと思いました。
あと、「ベイズ初めてです!」という新入りの方とかには慣れ親しんでもらうには良さそうですね。lm関数レベルで実行できてしまうので。
今回、mc-stan.orgの配下にあるページなどを漁る過程で、ベイズ推定結果の可視化などで知らないことにも色々と出会えたので、今後も読み進めていきます。
追記
2018-09-10: Stanを使って変数選択したいにprojpredというパッケージが紹介されており、これを使えば、情報量基準に従った変数選択を簡単に行えるそうです。こうなると、「ベイズ推定に慣れ親しんでいない頻度主義系のソフトウェアユーザー」に限らず多くの人が幸せになれるパッケージなのかもしれませんね。
参考情報
Using the loo package (version >= 2.0.0)
Leave-one-outクロスバリデーションの2つのデメリット、からの解決方法
stan_glmer | Bayesian Generalized Linear Models With Group-Specific Terms Via Stan
WAICを計算してみる
Package ‘bayesm’
Hierarchical Partial Pooling for Repeated Binary Trials
Leave-one-out cross-validation for non-factorizable models
priors | Prior Distributions And Options
StanとRでベイズ統計モデリング (Wonderful R)