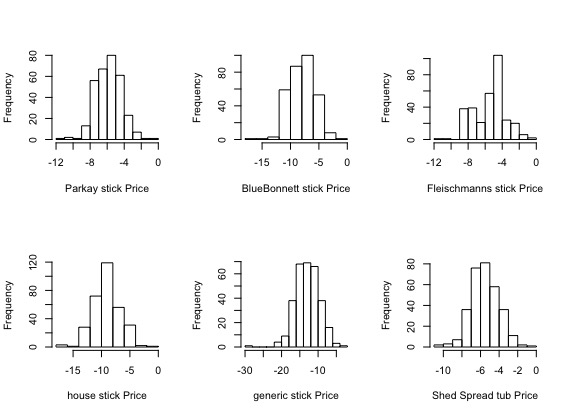
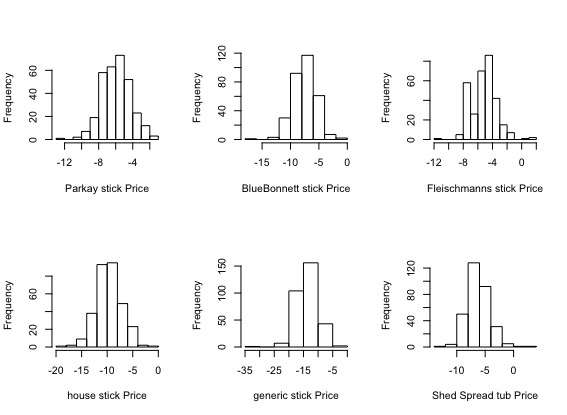
前回の分析では、価格への反応係数の事前分布が正規分布を仮定したモデルを用いていましたが、事後分布から多峰性が観察されました。そこで今回は、各個人の価格への反応係数の事前分布が混合ガウス分布に従うとした場合の事例を扱いたいと思います。
データのおさらい
データ自体は前回のブログと同じですが、先日のTokyo.Rで松浦さんがオススメしていたGGallyパッケージのggpairs関数を用いて、今回扱うデータを可視化してみます。
まず、購買したマーガリンのブランド選択(6ブランド分)と、購入した価格(ドル)からなるデータセットの可視化をすると以下のようになります。
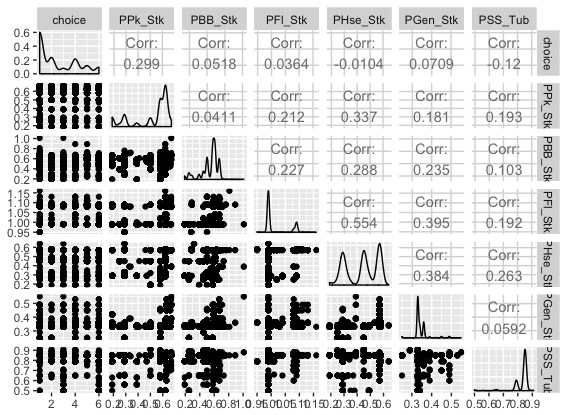
1つ目のブランドが最も多く選択されているようです。購入価格の分布は、ブランドによって多峰性がありそうです。
続いて、家計ごとの属性(家族構成、学歴、職位、退職の有無など)からなるデータセットの可視化をすると以下のようになります。
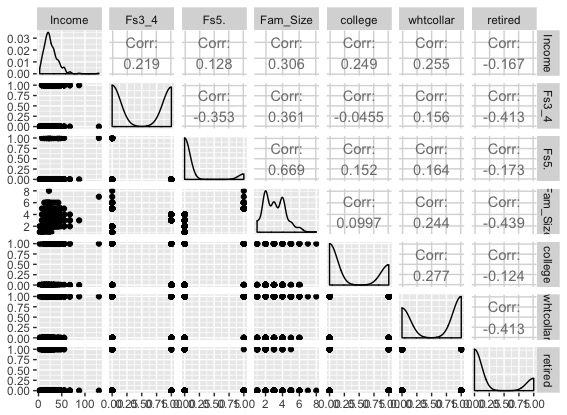
ほとんどダミー変数なので面白みには欠いていますね。ホワイトカラーの家計が多く、退職していない家計が多く、学歴が低い人が多いようです。年収に関しては対数正規分布に従ってそうです。
モデル
前回と同様に、「Bayesian Statistics and Marketing」の5章に載っている混合ガウスを想定した階層ベイズモデルを扱います。
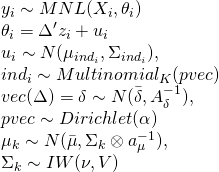
yi ∼ MNL(Xi, βi) は購買レコードごとの意思決定が多項ロジスティック回帰モデルに従うということを意味し、βiは(説明変数の数×1)のベクトルとなります。
βi = Z∆[i,] + ui は購買レコードごとの価格にかかってくる係数で、その係数が家計の属性データに係数Δ(家計の数×属性データからなる説明変数の数)をかけ合わせたものと潜在的な項の和となります。なお、ここでの属性データには定数項を含めていません。係数Δは平均deltabar、分散A_delta^-1の多変量正規分布に従います。一方で、潜在的な項は平均µind、分散Σindの多変量正規分布に従います。この平均や分散に振られているindが、混合正規分布のパラメータの通し番号となり、多項分布に従います。この多項分布の割当確率がディリクレ分布に従います。最後に混合正規分布の各パラメータは、平均は正規分布に分散は逆ウィシャート分布に従います。
前回との大きな違いは、価格の係数の一部である、潜在的な項において、混合正規分布が仮定されているところになります。
ちなみに、モデルに関しての詳細はbayesmパッケージのマニュアルの61ページ目に記載されていました。
今回のモデルのDAG
Pythonのdaftというモジュールを使うことで、非常に簡単に今回のモデルのDAG(有向非巡回グラフ)を描くことができます。
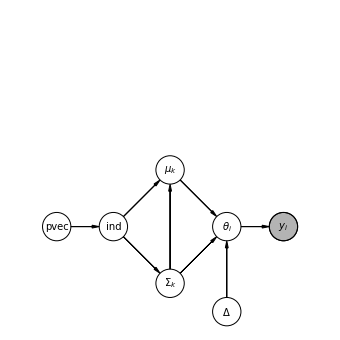
今回はこちらのPythonコードで描けました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
import daft from matplotlib import rc pgm = daft.PGM(shape=[6,6]) # Nodes pgm.add_node(daft.Node("pvec", r"pvec",1, 2)) # 名前 ラベル 座標(横、縦) pgm.add_node(daft.Node("ind", r"ind",2, 2)) pgm.add_node(daft.Node("sigma", r"$\Sigma_k$",3, 1)) pgm.add_node(daft.Node("mu", r"$\mu_k$",3, 3)) pgm.add_node(daft.Node("theta", r"$\theta_i$",4, 2)) pgm.add_node(daft.Node("delta", r"$\Delta$",4, 0.5)) pgm.add_node(daft.Node("y", r"$y_i$",5, 2,observed=True)) # Edges pgm.add_edge("pvec", "ind") pgm.add_edge("ind", "sigma") pgm.add_edge("ind", "mu") pgm.add_edge("sigma", "mu") pgm.add_edge("sigma", "theta") pgm.add_edge("mu", "theta") pgm.add_edge("delta", "theta") pgm.add_edge("theta", "y") pgm.render() pgm.figure.savefig("Hierachical_Models_ForMixtureNormal.png") |
stanコード
今回扱ったstanコードとなります。誤りがある場合はお知らせしていただけると幸いです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
data{ int<lower=0> N_x; // 購買レコードの数 int<lower=0> N_z; // 家計の数 int<lower=0> p_x; // 購買レコードの項目数 int<lower=0> p_z; // 家計の属性データの項目数 int y[N_x]; // 選択肢 matrix[N_x, p_x] X; // 説明変数 matrix[N_z, p_z] Z; // 家計の属性データ int<lower=0> hhid[N_x]; // 家計ID int K; // 混合ガウス分布の要素数 } transformed data{ real nu; matrix[p_x, p_x] I; // 購買レコードの説明変数の数の正方行列 matrix[p_x, p_x] J; // 属性データの説明変数の数の正方行列 nu = p_x + 3; // 説明変数の項に3を足す I = diag_matrix(rep_vector(1, p_x)); // 1を繰り返しp_x個並べた対角行列を作成 J = diag_matrix(rep_vector(1, p_x)); } parameters{ vector[p_x] theta_ast[N_z]; // 説明変数の数だけある、購買ごとのパラメータ matrix[p_z, p_x] Delta; // 属性データの説明変数の数×購買データの説明変数の数だけのパラメータ vector[p_x] u[N_z]; // 購買レコードごとのパラメータ vector[p_x] mu[K]; // 混合分布を構成する平均値 cov_matrix[p_x] Sigma[K]; // 共分散行列 simplex[K] pi[N_z]; // シンプレックス(各要素が[0,1]の範囲で合計が1という条件を満たす。) } transformed parameters{ vector[p_x] theta[N_z]; #家計の数だけの係数ベクトル for(i in 1:N_z){ // 家計の数だけ繰り返す theta[i] = theta_ast[i] + Delta' * Z[i]'; // 係数は家計属性ごとの特徴に異質なDeltaとbeta_astの和で決まる } } model{ real ps[K]; // 混合正規分布の対数 for(i in 1:N_x){ // 購買レコードの数だけ繰り返す y[i] ~ categorical(softmax(theta[hhid[i]] .* to_vector(X[i]))); //カテゴリカル分布にsoftmaxを組み合わせて多項ロジスティック回帰を行う pi[hhid[i]] ~ dirichlet(rep_vector(2, K)); for(k in 1:K){ // 混合分布の構成要素の数だけ繰り返す ps[k] = log(pi[hhid[i]][k]) + multi_normal_lpdf(theta_ast[hhid[i]] | mu[k], Sigma[k]); } target += log_sum_exp(ps); // 離散パラメータを消去した形で対数尤度を表現する際に必要な計算(周辺化消去)。 } for(k in 1:K){ // 混合パラメータの数だけ繰り返す mu[k] ~ multi_normal(rep_vector(0, p_x), 100*Sigma[k]); Sigma[k] ~ inv_wishart(nu, nu*I); } for(i in 1:p_z){ // 家計の属性データの数だけ繰り返す Delta[i] ~ multi_normal_cholesky(rep_vector(0, p_x), 100*J); } } |
stanをキックするためのコードです。先人が書かれた混合ガウスのスクリプトをHMCで実行した際に26時間ほどかかったので、今回はより複雑なモデルであることから、変分ベイズ法による推定を行ってみることにしました。松浦さんの教科書にあるように、vb関数を用いて変分ベイズ推論を行っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 |
library(bayesm) library(tidyverse) library(rstan) library(GGally) rstan_options(auto_write = TRUE) options(mc.cores = parallel::detectCores()) data("margarine") #1,2,3,4,5,7の商品に関してデータを抽出し、家計IDごとにカウントし、5件以上のものに絞る。 hhid_selected <- margarine$choicePrice %>% filter(choice %in% c(1,2,3,4,5,7)) %>% group_by(hhid) %>% summarise(purc_cnt = n()) %>% filter(purc_cnt >= 5) #今回扱う商品のカラムだけを抽出し、先ほど絞ったユーザーのリストに合致するデータでフィルターする。 choicePrice.selected <- margarine$choicePrice %>% filter(choice %in% c(1,2,3,4,5,7) & hhid %in% hhid_selected$hhid) #並べにくいので7を6に置き換える。 choicePrice.selected$choice[choicePrice.selected$choice == 7] <- 6 #家計ごとに関する属性データの抽出 demos.selected <- margarine$demos %>% filter(hhid %in% hhid_selected$hhid) #データサイズ N <- nrow(choicePrice.selected) #選択肢の数(特に使っているデータではない。) p <- n_distinct(choicePrice.selected$choice) #被説明変数 y <- choicePrice.selected$choice #説明変数 X <- choicePrice.selected %>% select(3,4,5,6,7,9) #家計の属性データから家計IDを除く Z <- demos.selected %>% select(-hhid) #可視化 ggpairs(choicePrice.selected %>% select(2,3,4,5,6,7,9)) ggpairs(Z) #家計の属性データから家計IDを抽出し、1から行数までのインデックスを付与する。 hhid_index <- demos.selected %>% select(hhid) %>% mutate(ind = seq(1,nrow(demos.selected))) #購買データの家計IDを抽出し、先ほどのインデックスとjoinする hhid_x <- choicePrice.selected %>% select(hhid) %>% left_join(hhid_index) #stanで扱うデータリストの作成 d.dat <- list(N_x=nrow(X), N_z=nrow(Z), p_x=ncol(X), p_z=ncol(Z), y=y, X=X, Z=Z, hhid = hhid_x$ind, K = 3) #推定 stanmodel <- stan_model(file = "Hierarchical_Mixture.stan") d.fit_vb <- vb(stanmodel, data=d.dat, seed=123) |
実行結果
今回はK={1,3,5,10}の混合要素数で推定を行いました。
Kが小さいと散らばりが比較的小さそうに見えます。逆に、Kが大きくなると散らばりが出てくるようです。
おわりに
2回に渡って、マーケティングデータを用いたベイズ統計モデリングを学んできましたが、数式からstanコードに落とし込む作業の際に、stanの関数をある程度知らないとやりにくいという至極当然なことを実感しました。これまでに使ってきたstanの関数は限られたものしか扱っていなかったと言えます。特に今回は離散パラメータをstanで扱うパーツがあったので、先行研究や松浦さんの本を読みながらの手探りが多かったです。
あと、複雑な階層ベイズモデルを扱う際に、頭の中を整理しないと手が止まってしまう感じがあったので、数式と対応するコードを横に並べながら進めました。
マーケティングにおいては、顧客の属性ごとに多峰性のあるような事例を扱うことが多く、かつ各々のサンプルサイズも期待できないことが多いので、今回の学びを分析業務で試してみたいと思います。
参考情報
Bayesian Statistics and Marketing (Wiley Series in Probability and Statistics)
Package ‘bayesm’
Multivariate Gaussian Mixture Model done properly
StanとRでベイズ統計モデリング (Wonderful R)
機械学習スタートアップシリーズ ベイズ推論による機械学習入門 (KS情報科学専門書)
daftでグラフィカルモデル