はじめに
ゴールデンウィークで実家に持ち込む本としてチョイスしたのが、2005年出版の「Bayesian Statistics and Marketing」です。大学院のときに購入して、ちょっとしか読んでませんでした。
この本は、字面の通りマーケティング関連の分析に関してベイズ統計を使ってアプローチするというもので、この書籍のために作られた、Rのbayesmというパッケージの紹介もあり、理論だけでなくRで実践することもできます。1章から7章までの全ての分析事例に対して実行可能な関数が用意されています。(CRANにあるdocumentも120p程度と割と大きめのパッケージです。)
和書で言うと、東北大学の照井先生の「ベイズモデリングによるマーケティング分析」などがありますが、その82pでもBayesian Statistics and Marketingとbayesmパッケージが紹介されています。
今回は、5章に載っている階層ベイズモデルを用いた、家計の異質性を考慮したブランド選択モデルの分析を紹介します。加えて、GitHubでstanによる再現を試みている方がいらっしゃったので、その方のコードの紹介も行います。
最近はこれまで以上にベイズ統計が流行ってきていますが、マーケティング×ベイズの書籍は限られている印象なので、少しでもリサーチのお役に立てれば幸いです。
目的
マーガリンの購買データから、ブランドごと、家計ごとのマーガリン価格に対しての反応の違いを明らかにしたい。
データ
bayesmパッケージにある、margarineデータ。data(margarine)で呼び出せ、詳細はcranのドキュメントに載っています。
Household Panel Data on Margarine Purchasesには、516家計の購買データと、家計ごとのデモグラフィック情報が収められています。1991年の論文のデータとなるので、かなり昔のデータです。
- 購買データは価格(USドル)と選択したブランドのID(10種類)
- デモグラフィック情報はfamily size(家族構成)、学歴、職位、退職の有無などのダミー変数
今回の事例では、5回以上購買した家計に限定して分析しているため、
313家計・3405の購買レコードからなるデータセットとなります。
モデル
- 家計ごとに異なる、マーガリン価格に対する反応を想定。各マーガリンのブランドの価格に対するパラメータの数は家計の数だけある。
- 価格に対する反応は家計の属性によっても決まる。
という前提に立ち、以下のセッティングで推論していきます。 - 6つのブランド選択に関する多項ロジスティックモデル(カテゴリカル分布とsoftmax関数の適用)
- 1階層目はブランドごとの価格を説明変数とし、価格に対する反応係数をかけ合わせたものを多項ロジスティックモデルの入力とする。
- 2階層目はブランドの価格に対する反応係数が家計ごとの定数項と属性データに属性ごとの係数をかけ合わせたものからなる。
- 家計ごとの定数項は平均0、分散V_betaの正規分布に従う。
- 属性ごとの係数は平均vec(delta_bar)、分散V_betaクロネッカーのデルタA^(-1)の正規分布に従う。
- 分散V_betaは平均υ、分散Vの逆ウィシャート分布に従う。
- A = 0.01、υ = 6 + 3 = 9、V = υI(Iは単位行列)
コード
kefitsさんがいくつかの章に登場するbayesmでの実践例をstanに書き直されているようですので、そちらのコードで学ばせていただこうと思います。
https://github.com/kefits/Bayesian-Statistics-and-Marketing
以下が、stanのコードとなっています。ここでは、Hierarchical_MNL.stanとして保存します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
data{ int<lower=0> N_x; // 購買レコードの数 int<lower=0> N_z; // 家計の数 int<lower=0> p_x; // 購買レコードの項目数 int<lower=0> p_z; // 家計の属性データの項目数 int y[N_x]; // 選択肢 matrix[N_x, p_x] X; // 説明変数 matrix[N_z, p_z] Z; // 家計の属性データ int<lower=0> hhid[N_x]; // 家計ID } transformed data{ real nu; matrix[p_x, p_x] I; // 説明変数の数の正方行列 nu = p_x + 3; // 説明変数の項に3を足す I = diag_matrix(rep_vector(1, p_x)); // 1を繰り返しp_x個並べた対角行列を作成 } parameters{ vector[p_x] beta_ast[N_z]; // 説明変数の数だけある、家計ごとのパラメータ matrix[p_z, p_x] Delta; // 属性データの説明変数の数×購買データの説明変数の数だけのパラメータ cov_matrix[p_x] V_b; // 共分散行列 } transformed parameters{ vector[p_x] beta[N_z]; #家計の数だけの係数ベクトル matrix[p_x, p_x] L_b; #共分散行列(beta(家計ごとの係数の共分散)) matrix[p_x, p_x] L_d; #共分散行列(delta(属性データの係数の共分散)) L_b = cholesky_decompose(V_b); // 共分散行列のコレスキー因子をもとめる L_d = cholesky_decompose(100*V_b); // 共分散行列に0.01で割ったもののコレスキー因子をもとめる for(i in 1:N_z){ beta[i] = beta_ast[i] + Delta' * Z[i]'; // 係数は家計属性ごとの特徴に異質なDeltaとbeta_astの和で決まる } } model{ for(i in 1:N_x){ y[i] ~ categorical(softmax(beta[hhid[i]] .* to_vector(X[i]))); //カテゴリカル分布にsoftmaxを組み合わせて多項ロジスティック回帰を行う } for(i in 1:p_z){ Delta[i] ~ multi_normal_cholesky(rep_vector(0, p_x), L_d); // コレスキー因子(L_d)を引数にとる多変量正規分布(推定の高速化のために用いることがある。) } beta_ast ~ multi_normal_cholesky(rep_vector(0, p_x), L_b); // コレスキー因子(L_b)を引数にとる多変量正規分布 V_b ~ inv_wishart(nu, nu*I); // 正規分布の共分散行列の共役事前分布として逆ウィシャート分布を利用 } |
以下はstanをキックするためのRコードです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
library(bayesm) library(dplyr) library(rstan) rstan_options(auto_write = TRUE) options(mc.cores = parallel::detectCores()) data("margarine") #1,2,3,4,5,7の商品に関してデータを抽出し、家計IDごとにカウントし、5件以上のものに絞る。 hhid_selected <- margarine$choicePrice %>% filter(choice %in% c(1,2,3,4,5,7)) %>% group_by(hhid) %>% summarise(purc_cnt = n()) %>% filter(purc_cnt >= 5) #今回扱う商品のカラムだけを抽出し、先ほど絞ったユーザーのリストに合致するデータでフィルターする。 choicePrice.selected <- margarine$choicePrice %>% filter(choice %in% c(1,2,3,4,5,7) & hhid %in% hhid_selected$hhid) #並べにくいので7を6に置き換える。 choicePrice.selected$choice[choicePrice.selected$choice == 7] <- 6 #家計ごとに関する属性データの抽出 demos.selected <- margarine$demos %>% filter(hhid %in% hhid_selected$hhid) #データサイズ N <- nrow(choicePrice.selected) #選択肢の数(特に使っているデータではない。) p <- n_distinct(choicePrice.selected$choice) #被説明変数 y <- choicePrice.selected$choice #説明変数 X <- choicePrice.selected %>% select(3,4,5,6,7,9) #家計の属性データから家計IDを除く Z <- demos.selected %>% select(-hhid) #定数項を1列目に追加する Z <- data.frame(intercept = rep(1, nrow(Z))) %>% bind_cols(Z) #家計の属性データから家計IDを抽出し、1から行数までのインデックスを付与する。 hhid_index <- demos.selected %>% select(hhid) %>% mutate(ind = seq(1,nrow(demos.selected))) #購買データの家計IDを抽出し、先ほどのインデックスとjoinする hhid_x <- choicePrice.selected %>% select(hhid) %>% left_join(hhid_index) #stanで扱うデータリストの作成 d.dat <- list(N_x=nrow(X), N_z=nrow(Z), p_x=ncol(X), p_z=ncol(Z), y=y, X=X, Z=Z, hhid = hhid_x$ind) #推定 d.fit <- stan("../Chapter5/Hierarchical_MNL.stan", data = d.dat, iter = 500, chains = 4) |
実行結果
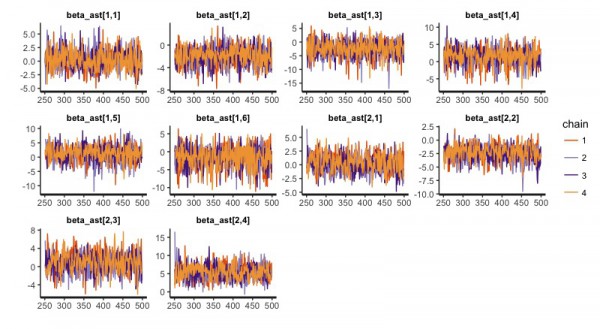
Core i5、8GBメモリのMacBook Proで40分ほどかかりました。
traceplot(d.fit)で以下のように4回の試行結果が描かれますが、収束しているようです。
summary関数を使えばわかりますが、3913行ものパラメータたちのサマリーが得られます。
- 313家計の家計ごとのブランドに対するパラメータ(1878個)
- 313家計の家計ごとのブランドに対する潜在パラメータ(1878個)
- 6ブランドの係数の共分散行列(36個)
- 6ブランドの係数の分散のハイパーパラメータの行列(36個)
- 6ブランドの属性データ(8つ)に対する係数(48個)
- 6ブランドの属性データに対する係数の共分散行列(36個)
- lp(log posterior(確率密度の和でモデル比較で扱う。))(1個)
64番目の家計の各ブランドの価格に対する係数の分布を確認すると、4番目・5番目のブランドの係数が他のブランドに比べて小さいことがわかります。
続いて、家計ごとの係数に関して集計し、係数ごとの相関係数を見てみると、各ブランドごとに正の相関、負の相関がありそうです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
#トレースプロット traceplot(d.fit) #係数のサマリー summary_table <- summary(d.fit)$summary draws <- extract(d.fit) beta <- as.data.frame(draws$beta) Delta <- as.data.frame(draws$Delta) V_b <- as.data.frame(draws$V_b) hhid_info <- inner_join(hhid_index, hhid_selected) # 1000行*313列のデータを313000行*1列のデータにしたい。 for (i in 1:6) { nam <- paste("beta", i, sep = "") assign(nam, beta[,(1+313*(i-1)):(313*(i))] %>% tidyr::gather(key, value)) } beta_matrix <- beta1 %>% bind_cols(beta2,beta3,beta4,beta5,beta6) beta_matrix <- beta_matrix %>% select(-starts_with("key")) #相関係数 cor(beta_matrix) value value1 value2 value3 value4 value5 value 1.0000000 0.5902734 0.4864998 -0.1798877 -0.4781558 0.3188025 value1 0.5902734 1.0000000 0.6134343 -0.2484286 -0.4441728 0.2002954 value2 0.4864998 0.6134343 1.0000000 0.1336322 -0.4512474 0.3663121 value3 -0.1798877 -0.2484286 0.1336322 1.0000000 0.6149186 0.2671819 value4 -0.4781558 -0.4441728 -0.4512474 0.6149186 1.0000000 0.1591574 value5 0.3188025 0.2002954 0.3663121 0.2671819 0.1591574 1.0000000 |
最後に、家計ごとに集計した、ブランドに対する価格反応係数の事後分布を描きます。

多峰性などはなく、正規分布に従っているようです。他のブランドと比較して、5番目の係数が小さいようです。
というのは誤りで、一週間後に気づいたのですが、家計ごとのブランドごとの係数の事後分布の平均値をプロットするべきでした。
正しくはこちらです。
事前情報として正規分布を仮定していましたが、係数に関して正規分布に従っていません。
そのため、事前情報として対称性のあるような正規分布を扱うのは適切ではなさそうです。
おわりに
2005年の本とは言え、十分に使いみちのある本だと思いました。まだまだ扱いきれていないですが、引き続き勉強していきます。
この本にはケーススタディが5つほどあるのですが、それのstanコード化などをしていけばかなり力がつくような気がします。
マーケティングの部署で働くデータアナリストにとって、マーケティング×ベイズの話は非常にモチベーションの上がるところなので、こういう文献を今後も見つけていきたい。
参考文献
Bayesian Statistics and Marketing (Wiley Series in Probability and Statistics)
Bayesian Statistics and Marketingのサポートサイト
ベイズモデリングによるマーケティング分析
StanとRでベイズ統計モデリング (Wonderful R)
RStanのおさらいをしながら読む 岩波DS 1 Shinya Uryu
Stanのlp__とは何なのか うなどん
‘LP__’ IN STAN OUTPUT
Package ‘bayesm’