松浦さんの『StanとRでベイズ統計モデリング』の8章の階層ベイズがすごくわかりやすいなぁと思いつつも、自分の持っているデータで試していなかったので、これを機に実践してみようと思います。
やや変数を追加しているくらいで大した変更点はありませんが、題材としては当ブログのアクセスログにおける直帰率に関するデータで、どのような要素が直帰率に影響を与えるのかを分析します。
目次
・モデル概要
・前処理
・推定
・結果(非階層モデルとの比較)
・参考文献
モデル概要
モデルは8章のロジスティック回帰の階層モデルに一部変数を追加していますが、ほぼそのままです。記事ごとのパラメータやリファラーごとのパラメータを想定しています。
Nは記事数でnはそのインデックス、Cはリファラーの数でcはそのインデックス、Iはログとして残っているセッションの数でiはそのインデックスとなっています。hatebuは記事のはてぶ数、stringlineは記事の行数、holidayは休日or祝日ダミー変数、daytimeは12:00~18:00なら1をとるダミー変数、revisitedは再訪問ユーザーなら1を取るダミー変数となっています。記事ごと・リファラーごとに直帰のしやすさが違う(パラメータが従う正規分布のパラメータがそれぞれ異なる)という仮定のもとに立ったモデルとなります。
$$x[i] = b_{1} + x_{記事}[記事ID[i]] \\ + x_{リファラー}[リファラーID[i]] + x_{セッション}[i] $$
$$q[i] = inverselogit(x[i]) $$
$$Y[i] \sim Bernoulli(q[i]) $$
$$x_{記事}[n] = b_{2}hatebu + b_{3}stringline[n] \\ + b_{記事間の差}[n] $$
$$b_{記事間の差}[n] \sim Normal(0, \sigma_{記事番号}) $$
$$x_{リファラー}[c] = b_{リファラー間の差}[c] $$
$$b_{リファラー間の差}[c] \sim Normal(0, \sigma_{リファラー番号}) $$
$$x_{セッション}[i] = b_{4}holiday[i] + b_{5}divice[i] \\ + b_{6}daytime[i] + b_{7}revisited[i] $$
前処理
GAのAPIからデータを取得して1セッション1記事になるようにデータを作成しています。数ヶ月で25000件ほどデータがあったのですが、計算に時間がかかるので、データ数を2400件くらいにサンプリングしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
library(RGA) library(tidyverse) library(Nippon) authorize() prof <-list_profiles() start_date <- "2017-04-01" end_date <- "2017-10-20" accesslogdata <- get_ga(profileId = prof$id[2], start.date = start_date, end.date = end_date, dimensions = "ga:pagePath, ga:dateHourMinute, ga:deviceCategory, ga:userType, ga:referralPath, ga:fullReferrer", sort = "-ga:sessions", metrics = "ga:sessions,ga:bounces", fetch.by = "day") #reshape_url accesslogdata$pagePath <- vapply(strsplit(accesslogdata$pagePath,"\\?"), `[`, 1, FUN.VALUE=character(1)) accesslogdata <- accesslogdata %>% filter(grepl(x = pagePath,"/archives/[0-9]+$")) accesslogdata$pagePath <- gsub(accesslogdata$pagePath,pattern = "/archives/",replacement = "article_") accesslogdata_filtered <- accesslogdata %>% filter(sessions == 1) accesslogdata_filtered <- accesslogdata_filtered %>% mutate(fullReferrer = ifelse(grepl(x = fullReferrer,'t.co/'),'twitter', fullReferrer)) %>% mutate(fullReferrer = ifelse(grepl(x = fullReferrer,'b.hatena.ne.jp/'),'b.hatena.ne.jp', fullReferrer)) %>% mutate(fullReferrer = ifelse(grepl(x = fullReferrer,'d.hatena.ne.jp/'),'d.hatena.ne.jp', fullReferrer)) %>% mutate(fullReferrer = ifelse(grepl(x = fullReferrer,'facebook.com/'),'facebook.com', fullReferrer)) #refferer list refferer_cat <- c("google", "(direct)", "twitter", "yahoo", "b.hatena.ne.jp", "facebook.com", "bing") daytime_cat <- c("12","13","14","15","16","17","18") #making weekday data and daytime data accesslogdata_filtered <- accesslogdata_filtered %>% filter(fullReferrer %in% refferer_cat) %>% mutate(date=as.Date(format(substr(accesslogdata_filtered$dateHourMinute,start = 1,stop = 12), format="%Y%m%d%"),format = "%Y%m%d")) %>% mutate(hourminutes = substr(accesslogdata_filtered$dateHourMinute,start = 9,stop = 10 )) %>% mutate(holiday = ifelse(is.jholiday(date), 1, 0)) %>% mutate(daytime = ifelse(hourminutes %in% daytime_cat, 1, 0)) %>% mutate(device = ifelse(deviceCategory == "desktop", 1, 0)) %>% mutate(revisited = ifelse(userType == "Returning Visitor", 1, 0)) selected_dataset <- accesslogdata_filtered %>% select(pagePath,fullReferrer, device,revisited,holiday,daytime,bounces) %>% filter(!(pagePath %in% c("article_10", "article_53") )) %>% bind_cols(rand =runif(nrow(selected_dataset), min = 0, max = 1)) %>% filter(rand <= 2400/nrow(selected_dataset)) referer_cat <- selected_dataset %>% select(fullReferrer) %>% distinct() %>% mutate(referer_id = 1:n()) article_cat <- selected_dataset %>% select(pagePath) %>% distinct() %>% mutate(article_id = 1:n()) selected_dataset <- selected_dataset %>% left_join(article_cat, by="pagePath") %>% left_join(referer_cat, by="fullReferrer") %>% select(-pagePath, -fullReferrer) article_data <- read_csv(file = "kamonohashiperry_text.csv") article_data$url <- gsub(article_data$url, pattern = "http://kamonohashiperry.com/archives/",replacement = "article_") article_data <- article_data %>% left_join(article_cat, by=c("url"="pagePath")) article_data <- article_data[!(is.na(article_data$article_id)),] |
推定
stanコードはこちらになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
data { int N; #the number of article int C; #the number of referer int I; #the number of log int<lower=0> hatebu[N]; real<lower=0> stringline[N]; int<lower=1, upper=N> article_id[I]; int<lower=1, upper=C> referer_id[I]; real<lower=0, upper=1> holiday[I]; real<lower=0, upper=1> device[I]; real<lower=0, upper=1> daytime[I]; real<lower=0, upper=1> revisited[I]; int<lower=0, upper=1> Y[I]; } parameters { real b[7]; real b_P[N]; real b_C[C]; real<lower=0> s_P; real<lower=0> s_C; } transformed parameters { real x_P[N]; real x_C[C]; real x_J[I]; real x[I]; real q[I]; for (n in 1:N) x_P[n] = b[2]*stringline[n] + b[3]*hatebu[n] + b_P[n]; for (c in 1:C) x_C[c] = b_C[c]; for (i in 1:I) { x_J[i] = b[4]*holiday[i] + b[5]*device[i] + b[6]*daytime[i] + b[7]*revisited[i]; x[i] = b[1] + x_P[article_id[i]] + x_C[referer_id[i]] + x_J[i]; q[i] = inv_logit(x[i]); } } model { for (n in 1:N) b_P[n] ~ normal(0, s_P); for (c in 1:C) b_C[c] ~ normal(0, s_C); for (i in 1:I) Y[i] ~ bernoulli(q[i]); } |
rstanを用いたstan実行用のRコードです。ヴァイオリンプロットで主要な係数の分布を見る処理も書かれています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
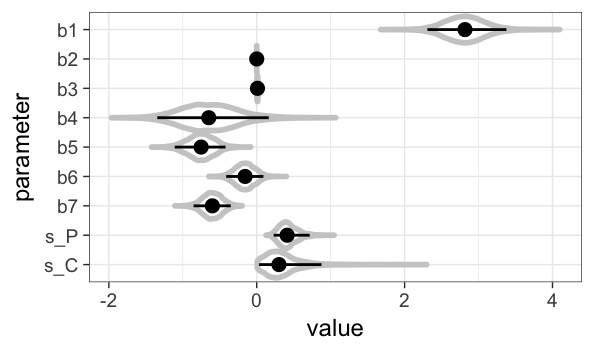
library(rstan) N <- nrow(article_cat) C <- nrow(referer_cat) I <- nrow(selected_dataset) data <- list(N = N, C = C, hatebu = article_data$hatebu, stringline = article_data$str_lines, article_id = selected_dataset$article_id, referer_id = selected_dataset$referer_id, holiday = selected_dataset$holiday, device = selected_dataset$device, daytime = selected_dataset$daytime, revisited = selected_dataset$revisited, Y = selected_dataset$bounces) fit <- stan(file = "model/model8-8_access_analysis.stan", data = data, pars = c("b", "b_P", "b_C", "s_P", "s_C", "q"), seed = 1234) source('../common.R') ms <- rstan::extract(fit) N_mcmc <- length(ms$lp__) param_names <- c('mcmc', paste0('b', 1:7), 's_P', 's_C') d_est <- data.frame(1:N_mcmc, ms$b, ms$s_P, ms$s_C) colnames(d_est) <- param_names d_qua <- data.frame.quantile.mcmc(x=param_names[-1], y_mcmc=d_est[,-1]) d_melt <- reshape2::melt(d_est, id=c('mcmc'), variable.name='X') d_melt$X <- factor(d_melt$X, levels=rev(levels(d_melt$X))) p <- ggplot() p <- p + theme_bw(base_size=18) p <- p + coord_flip() p <- p + geom_violin(data=d_melt, aes(x=X, y=value), fill='white', color='grey80', size=2, alpha=0.3, scale='width') p <- p + geom_pointrange(data=d_qua, aes(x=X, y=p50, ymin=p2.5, ymax=p97.5), size=1) p <- p + labs(x='parameter', y='value') p <- p + scale_y_continuous(breaks=seq(from=-2, to=6, by=2)) p |
結果
係数を見る限りは、符号の向きが確かなのはb5(PCダミー)とb7(再訪問ユーザーダミー)なので、PCの方が直帰しにくく、再訪問ユーザーの方が直帰しにくいという傾向があると考えることができます。
教科書ではAUCを非階層モデルと比較していましたので、比較してみようと思います。
AUCの計算を行うためのコードもGithubに載っていましたのでそちらを使います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
#calculate auc library(pROC) ms <- rstan::extract(fit) N_mcmc <- length(ms$lp__) spec <- seq(from=0, to=1, len=201) probs <- c(0.1, 0.5, 0.9) auces <- numeric(N_mcmc) m_roc <- matrix(nrow=length(spec), ncol=N_mcmc) for (i in 1:N_mcmc) { roc_res <- roc(selected_dataset$bounces, ms$q[i,]) auces[i] <- as.numeric(roc_res$auc) m_roc[,i] <- coords(roc_res, x=spec, input='specificity', ret='sensitivity') } quantile(auces, prob=probs) |
|
1 2 3 4 5 6 7 8 9 10 |
#ロジスティック回帰の階層ベイズ推定でのAUC > quantile(auces, prob=probs) 10% 50% 90% 0.6683084 0.6770603 0.6846594 #ロジスティック回帰のベイズ推定でのAUC > quantile(auces_non_hiral, prob=probs_non_hiral) 10% 50% 90% 0.5463287 0.5623697 0.5776898 |
80%が良いとされているAUCには程遠いですが、記事やリファラーごとの差を考慮しない非階層のものよりもAUCが高いと言えます。
ちなみに、教科書の例のAUCは80%ほどでした。
Webマーケのデータ分析においてロジットは汎用性が高いで、今回のコードを土台に色々と業務で試していこうと思います。
参考文献
StanとRでベイズ統計モデリング (Wonderful R)
ベイズ統計モデリング: R,JAGS, Stanによるチュートリアル 原著第2版