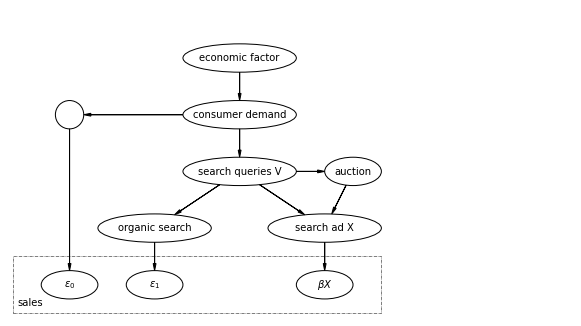
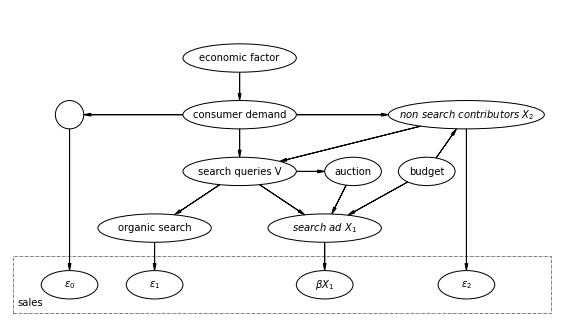
はじめに
最近、『施策デザインのための機械学習入門〜データ分析技術のビジネス活用における正しい考え方』が流行っていると思いますが、私も少しずつ読んでいます。
2019年ごろから勉強会などで知る機会のあったCountefactual Machine Learningですが、仕事で機械学習を使えば使うほどにその必要性を強く感じます。
書籍は体系的にまとまっていて非常に良いのですが、せっかく関心を持ったのでその源流と思われる論文やソースコードを漁ってみようと思いました。
今回、深ぼるのはこちらの論文です。
Recommendations as Treatments: Debiasing Learning and Evaluation
https://arxiv.org/abs/1602.05352
情報を漁る
arXivの方はAppendixついてなかったのでこちらの方がいいと思います。
https://www.cs.cornell.edu/people/tj/publications/schnabel_etal_16b.pdf
著者のスライドもありました。
https://www.cs.cornell.edu/~schnabts/downloads/slides/schnabel2016mnar.pdf
まずは読む
以下に読んだ際のメモを箇条書きします。
- レコメンドのデータは大体偏っている。偏ってアイテムの評価がされる。
- レコメンドに因果推論のアプローチを適用する。
- 傾向スコア(ランダムっぽさ)を用いた学習の重み付け
- バイアスの最小化?のアプローチ
- 行列分解による欠損値補完に対する重み付けをした。
- 色々なデータで試した。
- IPS(Inverse Propensity Score)で重み付けしたら誤差の不偏推定量を手に入れれる。
- 評価方法はMAE(Mean Absolute Error)とかDCG(Discounted Cumulative Gain)など
- 比較は一様に評価のデータが観察されると仮定したナイーブなモデルとで行う。
- 行列分解の次元数dとか、正則化項のラムダはハイパーパラメータとして扱う。
- 行列分解かつIPSで重みづけしたモデルはロバストに良い性能になった。
既出の参考資料を読む
ソースコード読む
コーネル大学のサイトに論文のソースコードがあったので、そちらの解読を試みます。
https://www.cs.cornell.edu/~schnabts/mnar/
そんなにソースコードは多くなかったです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
. ├── LICENSE.txt ├── README.txt ├── bin │ ├── test.py │ ├── train.py │ └── train.pyc ├── example │ ├── data │ │ ├── propensities.ascii │ │ ├── test.ascii │ │ └── train.ascii │ ├── test.bat │ ├── test.sh │ ├── train.bat │ └── train.sh ├── lib │ ├── Expt2.py │ ├── Expt2.pyc │ ├── Expt3.py │ ├── Expt3.pyc │ ├── MF.py │ ├── MF.pyc │ ├── Metrics.py │ ├── Metrics.pyc │ ├── __init__.py │ └── __init__.pyc └── requirements.txt 4 directories, 23 files |
train.sh
学習のバッチ処理
train.py
python ../bin/train.py –lambdas 0.008,25 –numdims 40 –ratings data/train.ascii –propensities data/propensities.ascii
- コマンドライン引数たち
- lambda:正則化パラメータ。デフォルトは’0.008,0.04,0.2,1,5,25,125′
- numdims:行列分解の次元数。デフォルトは’5,10,20,40′
- ratings:訓練用データの指定を行う(ASCII formatの行列)
- propensities:傾向スコアのデータの指定を行う(ASCII formatの行列)
- metric:デフォルトは’MSE’、MAEかMSEを選べる
MetricsのMSE/MAE関数を呼び出し、
Expt3のlearn関数を使って学習を実行する。
Metrics.py
- MSE関数
- ITEMWISE_METRICSを呼び出している
- MAE関数
- ITEMWISE_METRICSを呼び出している
- ITEMWISE_METRICS関数
- MSEかMAEかでnumpyのデータの形式を指定している。
- SET_PROPENSITIES関数を呼び出している
- 観測された評価と予測した評価の差分にIPWを掛け、観測誤差とする
- 累積の観測誤差を出す
- IPWの合計値で累積の観測誤差を割ったglobalNormalizerを計算して返す
- ユーザー単位での観測誤差の推定値をユーザー数で割ったuserNormalizedMetricを計算して返す
- アイテム単位での観測誤差の推定値をアイテム数で割ったitemNormalizedMetricを計算して返す
- SET_PROPENSITIES関数
- IPWがあればそれを使い、ない場合は出現割合を返している
- 観察されたデータを考慮して補間を行う(numpy.ma.arrayのmask)
Expt3.py
Expt2のINIT_PARAMS、MF_TRAIN、FINAL_TRAINを実行する
MFのPREDICTED_SCORESを実行する
- 処理の流れ
- もろもろの引数で学習の際の設定を受け取り
- 傾向スコアの逆数からIPWを計算し
- そのスコアを学習用データで補間し
- ランダムに並び替える
- 4-foldsでのクロスバリデーションを行う
- 学習を並列処理を行う
- 予測スコアから一番いいスコアのモデルを選ぶ
- 行列分解での機械学習を行う
- 行列分解での予測値を計算する
- 予測結果を返す
Expt2.py
MFのGENERATE_MATRIX、PREDICTED_SCORESを実行
- MF_TRAIN関数
- IPWを受け取って、上限下限などを調整
- それをMFのGENERATE_MATRIX関数に適用
- FINAL_TRAIN関数
- MF_TRAIN関数と似たような処理
- 交差検証してベストだったパラメータに適用する想定
- INIT_PARAMS関数
- 評価行列の欠損値を補間している
- 行列特異値分解を行っている
- その結果をstartTuple(初期値)として与えている
MF.py
- PREDICTED_SCORES関数
- バイアスがあるかどうかで分岐
- バイアスがあれば、元のスコアにユーザーのバイアス、アイテムのバイアス、グローバルなバイアスを足し合わせる
- バイアスがなければそのまま返す
- GENERATE_MATRIX関数
- 指標がMSEかMAEかで分岐
- MetricsのSET_PROPENSITIES関数を実行
- ユーザー単位での標準化やアイテム単位での標準化、全体での標準化のための計算をする
- 標準化の方法で分岐、傾向スコアを標準化する
- バイアスのモードで分岐
- 学習のための初期値としてのデータを設定
- 目的関数の最適化(最小化)を行う
- その結果を返す
- Mat2Vec関数
- 行列をパラメータのベクトルにする
- Vec2Mat関数
- パラメータベクトルを入力する
- ユーザーベクトル、アイテムベクトル、ユーザーバイアス、アイテムバイアス、グルーバルバイアスを返す
test.sh
テストのバッチ処理
test.py
python ../bin/test.py –test data/test.ascii –completed completed_ratings.ascii
- コマンドライン引数たち
- test:テスト用の評価データを指定する(ASCII formatの行列)
- completed:評価を埋めたい行列のファイル名を指定
MSEやらMAEの結果を返す。
所感
まず論文の内容ですが、大体のビジネスデータはRCTな状況で生み出されたものではないので、偏って観測されるのは当然ですが、その結果としてレコメンドのアルゴリズムの性能が落ちてしまうということが論文に記されていました。性能を落とさないためにも、傾向スコアを用いた重み付けによる機械学習が大事に思いました。ただ、傾向スコアの推定自体の精度も大事に思われるので、銀の弾丸ではないですが、バイアスから抜け出るヒントをいただけたという気持ちです。
そして、思ったよりもソースコードが長いと思ったのと、普段あまり使わないNumpyの関数を知ることができたのもよかったです。
理論の理解だけでなく、それを実現するためのソースコードを眺めるのも大事ですね。今後も論文をただ読むだけでなくソースコードの海に飛び込んでみようと思います。
参考リンク
numpy.reciprocal
maskedarray.generic
numpy.ma.getmask
numpy.clip
scipy.sparse.linalg.svds
numpy.ma.filled
scipy.optimize.minimize