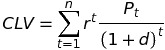顧客生涯価値(CLV:Customer Lifetime Value)を計算してくれるRのコード(Calculating Customer Lifetime Value with Recency, Frequency, and Monetary (RFM))があったので、今更感がありますが取り上げたいと思います。
目次
・顧客生涯価値の数式
・データセット
・関数
・データセットの読み込みと加工
・再購買率とRFMとの関係
・再購買率の推定
・顧客生涯価値の計算
・参考情報
顧客生涯価値の数式
t:年や月などの期間
n:顧客が解約するまでの期間合計
r:保持率(1-解約率)
P(t):t期に顧客から得られる収益
d:割引率
rは数式上では固定ですが、実際にはデモグラ属性(年齢、地理情報、職種など)や行動(RFMなど)や在職中かどうかなどの要因により変わりうるものだと考えられます。参考文献のブログでは、このrのロジスティック回帰による推定がなされています。
データセット
データ名:CDNow
概要:1997年の第一四半期をスタート時点とした顧客の購買行動データ
期間:1997年1月〜1998年6月
顧客数:23570
取引レコード数:69659
変数:顧客ID、購入日、購入金額
入手方法:DatasetsでCDNOW dataset (full dataset)をダウンロード
関数
参考文献にはgetDataFrame関数、getPercentages関数、getCLV関数の三つの関数が出てきますが、CLVの計算に必要なのはgetDataFrame関数、getCLV関数の二つです。getPercentages関数はRecencyなどに応じて細かく分析する際に用います。
getDataFrame関数・・・生のデータセットから、指定した期間に応じたRecencyのデータを作成する関数です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
getDataFrame <- function(df,startDate,endDate,tIDColName="ID",tDateColName="Date",tAmountColName="Amount"){ #日付について降順でデータフレームを並び替える df <- df[order(df[,tDateColName],decreasing = TRUE),] #開始期間の前と終了期間の後のデータを取り除く df <- df[df[,tDateColName]>= startDate,] df <- df[df[,tDateColName]<= endDate,] #重複したIDの行を除外して新しいデータフレームを生成する newdf <- df[!duplicated(df[,tIDColName]),] # 終了期間に対してのRecencyを計算する(最も小さい値は最も最近であることを示す) Recency <- as.numeric(difftime(endDate,newdf[,tDateColName],units="days")) # newdfデータフレームに日付の列を加える newdf <- cbind(newdf,Recency) # table関数やtapply関数の返す順番と揃うようにデータフレームをIDごとに並べ替える newdf <- newdf[order(newdf[,tIDColName]),] # 頻度を計算する fre <- as.data.frame(table(df[,tIDColName])) Frequency <- fre[,2] newdf <- cbind(newdf,Frequency) # 取引ごとの金額を計算する m <- as.data.frame(tapply(df[,tAmountColName],df[,tIDColName],sum)) Monetary <- m[,1]/Frequency newdf <- cbind(newdf,Monetary) return(newdf) } |
getPercentages関数・・・Recencyなどの回数に応じて、購入した顧客の割合などを計算するための関数です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
require(plyr) getPercentages <- function(df,colNames){ #指定した列の名前とBuyからなるベクトルの作成 Var <- c(colNames,"Buy") #指定した変数とBuyが合致する列だけを抽出 df <- df[,names(df) %in% Var,drop=F] #購買した回数に応じたデータ数を返す a <- ddply(df,Var,summarize,Number=length(Buy)) #回数に応じたデータ数に対して、全体の割合を返す b <- ddply(a, .(), .fun=function(x){ transform(x, Percentage=with(x,round(ave(Number,a[,names(a) %in% Var,drop=F],FUN=sum)/ave(Number,a[,names(a) %in% colNames,drop=F],FUN=sum),2))) }) #1列目を除外する b <- b[b$Buy==1,-1] return(b) } |
getCLV関数・・・Recency、Frequency、Monetary、購入者の数(1人と置く)、コスト(0としている)、期間、割引率、推定したモデルをもとにCLVを計算する関数です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
getCLV<-function(r,f,m,n,cost,periods,dr,pModel){ df<-data.frame(period=c(0),r=c(r),f=c(f),n=c(n),value=c(0)) for(i in 1:periods){ backstep<-df[df$period==i-1,] nrow<-nrow(backstep) for(j in 1:nrow){ r<-backstep[j,]$r f<-backstep[j,]$f n<-backstep[j,]$n p<-predict(pModel,data.frame(Recency=r,Frequency=f),type='response')[1] buyers<-n*p df<-rbind(df,c(i,0,f+1,buyers,buyers*(m-cost) / (1+dr)^i)) df<-rbind(df,c(i,r+1,f,n-buyers,(n-buyers)*(-cost) / (1+dr)^i )) } } return(sum(df$value)) } |
データセットの読み込みと加工
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# CDNOW_SAMPLE.txtを読み込む df <- read.table(file = "CDNOW_master.txt",header=F) # 取引ごと且つ顧客ごとに、ID、取引日、購入金額の列からなるデータフレームを生成する df <- as.data.frame(cbind(df[,1],df[,2],df[,4])) # 列名の変更 names <- c("ID","Date","Amount") names(df) <- names #日付の型の変更 df[,2] <- as.Date(as.character(df[,2]),"%Y%m%d") |
|
1 2 3 4 5 6 7 8 |
> head(df) ID Date Amount 1 1 1997-01-01 11.77 2 2 1997-01-12 12.00 3 2 1997-01-12 77.00 4 3 1997-01-02 20.76 5 3 1997-03-30 20.76 6 3 1997-04-02 19.54 |
再購買率とRFMとの関係
まず初めにデータセットを加工します。ロジットの推定における説明変数用のデータとして19970101〜19980228のデータを用い、被説明変数にあたる購入したかどうかのデータを19980301〜19980430のデータを用いて作ります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# 取引期間の範囲を指定する startDate_history <- as.Date("19970101","%Y%m%d") endDate_history <- as.Date("19980228","%Y%m%d") # 2ヶ月間の購入サイクルにあたる予測期間を指定する startDate_forcast <- as.Date("19980301","%Y%m%d") endDate_forcast <- as.Date("19980430","%Y%m%d") # getDataFrame関数でRFMデータに変換する history <- getDataFrame(df,startDate_history,endDate_history) forcast <- getDataFrame(df,startDate_forcast,endDate_forcast) # 購入サイクルを60日とし、Recencyを離散化する history$Recency <- history$Recency %/% 60 # Monetaryを10ドル単位で離散化する breaks <- seq(0,round(max(history$Monetary)+9),by=10) history$Monetary <- as.numeric(cut(history$Monetary,breaks,labels=FALSE)) # RFMのデータフレームに購入・非購入データを加える Buy <- rep(0,nrow(history)) history <- cbind(history,Buy) # Buyに関して、予測期間(1998/3/1~1998/4/30)の期間で再度購入しているならば1を返すようにする history[history$ID %in% forcast$ID, ]$Buy<-1 train <- history |
データを確認します。
|
1 2 3 4 5 6 7 8 |
> head(train) ID Date Amount Recency Frequency Monetary Buy 1 1 1997-01-01 11.77 7 1 2 0 2 2 1997-01-12 12.00 6 2 5 0 8 3 1997-11-25 20.96 1 5 3 0 13 4 1997-12-12 26.48 1 4 3 0 24 5 1998-01-03 37.47 0 11 4 0 25 6 1997-01-01 20.99 7 1 3 0 |
|
1 2 3 |
# getPercentages関数を用いて、Recency変数に基づいて購入者の割合を計算する colNames <- c("Recency") p <- getPercentages(train,colNames) |
|
1 2 3 4 5 6 7 8 9 10 |
> p Recency Buy Number Percentage 2 0 1 1180 0.45 4 1 1 581 0.28 6 2 1 279 0.22 8 3 1 198 0.17 10 4 1 163 0.14 12 5 1 249 0.05 14 6 1 316 0.03 16 7 1 13 0.03 |
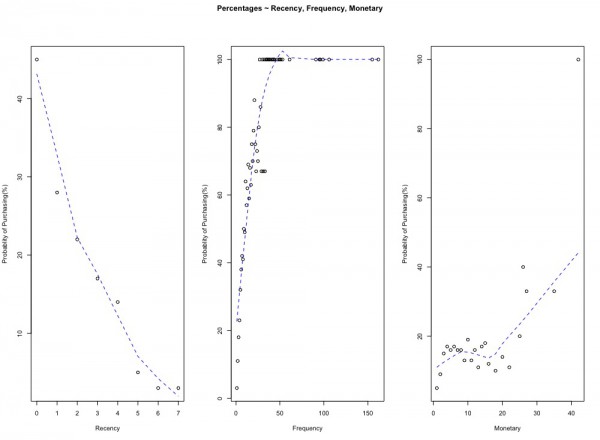
60日以内に購入した顧客(Recency=0)のうち、45%が再び購入しているようです。
|
1 2 3 |
# getPercentages関数を用いて、Monetary変数に基づいて購入者の割合を計算する colNames <- c("Monetary") p <- getPercentages(train,colNames) |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
> head(p,10) Monetary Buy Number Percentage 2 1 1 43 0.05 4 2 1 727 0.09 6 3 1 760 0.15 8 4 1 525 0.17 10 5 1 333 0.16 12 6 1 218 0.17 14 7 1 117 0.16 16 8 1 87 0.16 18 9 1 45 0.13 20 10 1 44 0.19 |
100ドル購入した顧客(Monetary=10)のうち、19%が再び購入しているようです。
|
1 2 3 |
# getPercentages関数を用いて、Frequency変数に基づいて購入者の割合を計算する colNames<-c("Frequency") p<-getPercentages(train,colNames) |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
> head(p,10) Frequency Buy Number Percentage 2 1 1 399 0.03 4 2 1 455 0.11 6 3 1 411 0.18 8 4 1 299 0.23 10 5 1 293 0.32 12 6 1 212 0.38 14 7 1 164 0.42 16 8 1 123 0.41 18 9 1 108 0.50 20 10 1 70 0.49 |
10回購入したことのある顧客(Frequency=10)は49%が再び購入しているようです。
再購買率の推定
RFM(Recency、Frequency、Monetary)のデータに基づいて、再購買率をロジスティック回帰によって推定し、予測確率を用いて顧客生涯価値を計算します。
|
1 2 3 |
# 再購買の割合をRecencyでロジスティック回帰 r.glm = glm(Percentage~Recency,family=quasibinomial(link='logit'),data=p) p_r <- p |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
> summary(r.glm) Call: glm(formula = Percentage ~ Recency, family = quasibinomial(link = "logit"), data = p) Deviance Residuals: Min 1Q Median 3Q Max -0.085865 -0.067551 0.000333 0.041373 0.116927 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.28538 0.11395 -2.504 0.0462 * Recency -0.47037 0.04035 -11.657 2.4e-05 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for quasibinomial family taken to be 0.005805806) Null deviance: 1.052105 on 7 degrees of freedom Residual deviance: 0.034439 on 6 degrees of freedom AIC: NA Number of Fisher Scoring iterations: 6 |
|
1 2 3 |
# 再購買の割合を頻度でロジスティック回帰 f.glm = glm(Percentage~Frequency,family=quasibinomial(link='logit'),data=p) p_f <- p |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
> summary(f.glm) Call: glm(formula = Percentage ~ Frequency, family = quasibinomial(link = "logit"), data = p) Deviance Residuals: Min 1Q Median 3Q Max -0.79432 -0.03744 0.10447 0.19982 0.52309 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -1.48217 0.21490 -6.897 6.05e-09 *** Frequency 0.12601 0.01139 11.067 1.67e-15 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for quasibinomial family taken to be 0.08078336) Null deviance: 25.652 on 55 degrees of freedom Residual deviance: 4.053 on 54 degrees of freedom AIC: NA Number of Fisher Scoring iterations: 7 |
|
1 2 3 |
# 再購買の割合をMonetaryでロジスティック回帰 m.glm = glm(Percentage~Monetary,family=quasibinomial(link='logit'),data=p) p_m <- p |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
> summary(m.glm) Call: glm(formula = Percentage ~ Monetary, family = quasibinomial(link = "logit"), data = p) Deviance Residuals: Min 1Q Median 3Q Max -0.40487 -0.16209 0.00298 0.15201 0.96271 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -2.61381 0.27229 -9.599 2.53e-09 *** Monetary 0.07482 0.01266 5.908 6.04e-06 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for quasibinomial family taken to be 0.06566381) Null deviance: 4.2966 on 23 degrees of freedom Residual deviance: 1.8027 on 22 degrees of freedom AIC: NA Number of Fisher Scoring iterations: 5 |
RecencyとFrequencyによるロジスティック回帰
|
1 2 |
model <- glm(Buy~Recency+Frequency,family=quasibinomial(link='logit'),data=train) pred <- predict(model,data.frame(Recency=c(0),Frequency=c(1)),type='response') |
|
1 2 3 |
> pred 1 0.2579282 |
顧客生涯価値の計算
推定したロジットを用いて、生涯価値を計算します。
|
1 2 |
# 3期間に関する顧客生涯価値の計算(Recency=0、Frequency=1、平均収益=100ドル、割引率=2%) v<-getCLV(0,1,100,1,0,3,0.02,model) |
|
1 2 |
> v [1] 63.91906 |
それではさっそく、1998年5月〜6月のデータを用いて、今回推定した顧客生涯価値が妥当なのかどうかを確かめたいと思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
#トレーニングデータをもとにCLVを計算する train_pred <- cbind(train,lifetimevalue=matrix(,nrow(train),1)) pb <- txtProgressBar(min = 1, max = nrow(train_pred), style = 3) for(i in 1:nrow(train_pred)){ train_pred$lifetimevalue[i] <- getCLV(train_pred$Recency[i],train_pred$Frequency[i],100,1,0,3,0.02,model) setTxtProgressBar(pb, i) } #1998年5月1日〜6月30日の間の取引データからIDと購入金額を集計する。 startDate_test <- as.Date("19980501","%Y%m%d") endDate_test <- as.Date("19980630","%Y%m%d") test <- getDataFrame(df,startDate_test,endDate_test) test_monetary <- dplyr::select(test,ID,Monetary) #予測したCLVと実際の取引金額のデータをマージする。 train_pred_2 <- data.frame(train_pred[,colnames(train_pred) %in% c("ID","lifetimevalue")]) train_pred_2 <- merge(train_pred,test_monetary,by = "ID",all=T) train_pred_2$Monetary.y[is.na(train_pred_2$Monetary.y)] <- 0 |
予測したCLVと実際の取引金額データを散布図で描き、回帰線を引く。
|
1 2 3 4 5 |
library(ggplot2) g <- ggplot(train_pred_2,aes (x = lifetimevalue,y = Monetary.y)) g <- g + geom_point(shape = 20,size = 0.8,na.rm = TRUE) g <- g + geom_smooth(method = glm) + xlab("lifetimevalue") + ylab("Monetary") plot(g) |
CLVが上がれば、1998年5月1日〜6月30日の間(未来)の取引金額が増すような傾向が出ています。
参考情報
RFM Customer Analysis with R Language
Calculating Customer Lifetime Value with Recency, Frequency, and Monetary (RFM)