目的
データサイエンス界隈の方がP値での意思決定に警鐘を鳴らしている昨今、施策実施に関するCVRの前後比較をχ2乗検定のP値を用いるのではなく、ベイズ統計学によるアプローチにチャレンジしてみたいと思いました。『基礎からのベイズ統計学』の8章で取り上げられていた比率データに対してのベイズ統計学的アプローチをもとに、stanを用いて事後分布から意思決定をするための進め方を紹介します。
進め方
・データの整形
・stanコード作成
・rstanでの引数の指定
・rでの可視化
データの特徴
Webマーケティング界隈では大変に多用するデータだと思いますが、実験を行ったユーザーに対しての開封・非開封、これまで通りのユーザーの開封・非開封の自然数からなるデータです。
stanコード
stanコードは
・dataブロック
・parametersブロック
・transformed parametersブロック(今回は不使用)
・modelブロック
・generated quantitiesブロック
からなります。
今回は自然数のデータであることから、ディリクレ分布を事前分布に設定するために、parametersブロックにおいてsimplexを指定しています。(教科書の比率データのものをそのまま使っています。)
modelは二項データしか出てこないので、二項分布を用いています。generated quantitiesブロックでは各々の比率、比率の差、比率の差が0を超える確率・0.01を超える確率、リスク比、リスク比が1を超える確率、オッズ比などを出力するようにしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
data{ int<lower=0> N[2]; #自然数からなるベクトルNの指定 int n[2,2]; #整数からなる行列nの指定 } parameters{ simplex[2] p[2]; #ディリクレ分布を事前分布に設定したもとでの確率pを指定 } model{ for(i in 1:2){ for(j in 1:2){ n[i,j] ~ binomial(N[j], p[j][i]); #二項分布 } } } generated quantities{ real p11; real p10; real p01; real p00; real d; real delta_over; real delta_over_onep; real RR; real RRover; real OR; p11 <- p[1][1]; p10 <- p[1][2]; p01 <- p[2][1]; p00 <- p[2][2]; d <- p11 - p01; #比率の差 delta_over <- if_else(d > 0,1,0); delta_over_onep <- if_else(d > 0.01,1,0); RR <- p11/p01; #リスク比 RRover <- if_else(RR > 2,1,0); OR <- (p11/p10) / (p01/p00); #オッズ比 } |
rコード
以下は、stanをrで実行し、ggplot2などで可視化するためのコードが記されています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
library(rstan) library (reshape) library (ggplot2) scr <- "model871.stan" #stanコード名 #カウントデータを用意します。 N <- c(1123, 1200) n <- structure(.Data = c(106, 1017, 46, 1154), .Dim = c(2, 2)) #stanで用いるデータの型に変換 data <-list(N=N, n=n) #パラメータの設定 par<-c("p","d","delta_over","delta_over_onep","RR","RRover","OR") #pは各々の比率 #dは比率の差 #delta_overは比率の差が0を超える確率 #delta_over_onepは比率の差が0.1を超える確率 #RRはリスク比 #RRoverはRRが1を超える確率 #ORはオッズ比 war<-1000 #バーンインの期間を指定しています。 ite<-11000 #試行回数をしていしています。 see<-12345 #乱数の種 dig<-3 #有効数字 cha<-1 #連鎖構成数 #stanの実行 fit <- stan(file = scr, data = data, warm=war, iter=ite, seed=see, pars=par,chains=cha) #結果の出力 print(fit,pars=par,digits_summary=dig) #事後分布の可視化 post <- extract (fit, permuted = F) m.post <- melt (post) graph <- ggplot (m.post, aes(x = value)) graph <- graph + geom_density () + facet_grid(. ~ parameters, scales = "free") + theme_bw() plot (graph) |
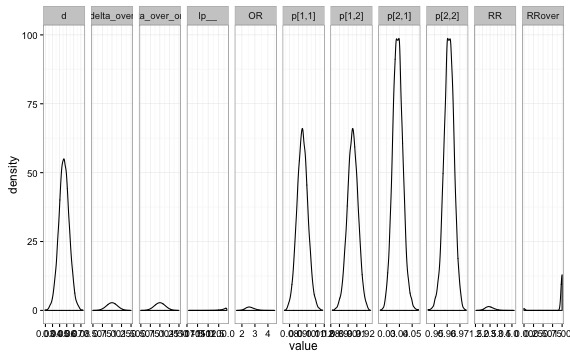
推定結果&可視化
今回の例では、実験を行ったユーザーのCVRの差が0以上の確率(delta_over)が1.0なので、ほぼ確実に差があると言えそうです。0.01以上差がある確率も1.0なので1%以上は差があると言えそうです。リスク比(RR)に関しては2.47と実験しない場合と比べて2.47倍程度CVを高めています。オッズ比(OR)は2.63とあるので、実験によるCV増大効果が2.63倍あると考えることができます。χ2乗検定では、二つの集団が独立かどうかを検定していますが、ベイズ統計学に従えば、「1%を超える確率」を算出することが容易なので、ディレクターなどに説明する際は圧倒的に理解を得られそうな気がします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
> print(fit,pars=par,digits_summary=dig) Inference for Stan model: model871. 1 chains, each with iter=11000; warmup=1000; thin=1; post-warmup draws per chain=10000, total post-warmup draws=10000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat p[1,1] 0.095 0.000 0.006 0.083 0.091 0.095 0.099 0.107 5645 1 p[1,2] 0.905 0.000 0.006 0.893 0.901 0.905 0.909 0.917 5645 1 p[2,1] 0.039 0.000 0.004 0.031 0.036 0.039 0.041 0.047 5488 1 p[2,2] 0.961 0.000 0.004 0.953 0.959 0.961 0.964 0.969 5488 1 d 0.056 0.000 0.007 0.042 0.051 0.056 0.061 0.071 5662 1 delta_over 1.000 0.000 0.000 1.000 1.000 1.000 1.000 1.000 10000 NaN delta_over_onep 1.000 0.000 0.000 1.000 1.000 1.000 1.000 1.000 10000 NaN RR 2.477 0.004 0.303 1.933 2.267 2.453 2.662 3.136 5454 1 RRover 0.955 0.003 0.207 0.000 1.000 1.000 1.000 1.000 5749 1 OR 2.633 0.005 0.341 2.026 2.396 2.606 2.842 3.377 5463 1 Samples were drawn using NUTS(diag_e) at Sun Mar 13 23:19:36 2016. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1). |
参考文献