2016年にバリアンがPNAS(Proceedings of the National Academy of Sciences of the United States of America)に投稿した”Causal Inference in Economics and Marketing”というペーパーを見つけました。内容的に非常にわかりやすかったし学びがあったので、要約して自分のためにメモを残しておきたいと思います。要約なんぞいらないという方はこちらのPDFを見ていただけると良いです。
修士が終わってからWebマーケティングの仕事をずっとしていますが、ABテストができるケースが多かったので因果推論が必要になる場面はあまりありませんでした。ただ、事業会社でしばしば行われるオフライン広告や社内の研修の効果に関してはABテストのような実験はできませんので、因果推論のニーズは「実は」高いと思います。ただ、広告を打つ主体・研修を進める主体がその分析のニーズがあるかというと全然そんなことはないと思います。今回のバリアンの素晴らしい記事をもとに因果推論の民主化をできると、説明の手間が省けるぶん世のデータサイエンティストは少しだけ楽になるかもしれません。
目次
・欠落変数の問題
・因果推論の重要なコンセプト
・因果効果を推定できる方法
・自然実験
・操作変数法
・回帰分断デザイン
・Difference in differences(DID)
・おわりに
・参考文献
欠落変数の問題
まずは以下のようなシンプルな線形モデルについて振り返ってみます。y_cはある都市でのサーフィン映画の一人あたりの売上、x_cはある都市でのサーフィン映画に関する広告支出を、bは係数、e_cは誤差項を表します。
![]()
この式を推定できれば広告主は何が嬉しいのかと言うと、1単位あたり広告支出を増やせば、どれくらいサーフィン映画の売上が増えるのかがわかるということです。
しかしながら、様々な都市を混ぜこぜしたデータからこの式を推定したものを使って、求まったbが10だとします。その際に、100円突っ込めば1000円儲かる、濡れ手で粟とはこのことや!状態が訪れるのでしょうか。
回帰分析には欠落変数の問題があり、欠落変数が説明変数と相関していると、濡れ手で粟とは言えない状況が起きうります。
まず、本来モデルに加えるべき変数がモデルに含まれていない場合、その変数はすべて誤差項に含まれることになります。
係数bの数式を確認してみると、
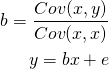
から、yを代入すると、
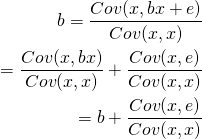
となります。右辺のbは真のbの係数とします。もし、誤差項eと説明変数が相関していれば、右辺二項目の影響により偏った推定量を得ることになります。つまり、本来モデルに加えるべき変数が漏れており、それが説明変数と相関している場合は、濡れ手で粟状態になるとは言えず、100円広告に突っ込んでも1000円儲かると期待することはできなくなります。せっかく推定したのに大損するという、非常に気の毒な結末があるでしょう。
釈迦に説法ですが、被説明変数と説明変数の両方に対して相関してしまう変数を交絡変数と呼びます。今回のサーフィン映画の場合、モデルに含まれていない変数として「サーフィンへの関心度」というものが考えられます。例えば、ハワイ州のホノルルのようなエリアではサーフィンが盛んですしサーフィン映画も人気になりえます。他方、ノースダコタ州のファーゴのような、群馬・栃木・埼玉・岐阜のような海なし県のようなエリアの場合、サーフィンもサーフィン映画も人気ではないでしょう。
ここでのサーフィンへの関心度は「サーフィン映画に対する広告支出」にも影響を与える可能性もありますし、そもそもの「サーフィン映画の興行収入」にも影響を与える可能性があります。
また、広告費自体は、映画の広告担当者が様々なドメイン知識を利用して意思決定しているのが普通で、都市に対してランダムに広告予算を割り振っているという、無能な運用者を想定することは難しいです。そのため、都市間でランダムに広告費が割り振られると考えるような分析者はあまり賢明ではないでしょう。現実世界において、人間が意思決定した結果のデータのほとんどが交絡変数を持つと考えられます。
因果推論の重要なコンセプト
因果推論における重要なコンセプトは、反実仮想と実際の結果との比較をすることです。この場合の反実仮想は処置されなかった場合の処置群の結果となります。

ランダム化実験が可能な場合、セレクションバイアスはゼロになります。そのため、ABテストなどでランダム出し分けができるWebマーケティングは因果推論が行いやすいのです。しかしながら、実務においてのランダム化実験や、ランダムでなくともそもそもの実験自体がハードルが高いケースが多いです。以降ではそのような現状を踏まえた上で、因果効果を推定するための方法を紹介します。
因果効果を推定するための方法
自然実験
自然実験は、手元のデータからランダムに近そうな事象があるのではないかを見出すというアプローチです。バリアンの例では、スーパーボウル(アメリカンフットボール)の試合での映画広告出稿に関して、ホームシティのチームの試合がそのスタジアムで開催される場合に、10~15%ほど観客が多いという前提があるとして、映画広告の出稿の意思決定をする際にどのチームがそのスタジアムで試合が行われるかわからないという点に着目していました。つまり、どのチームがどのスタジアムで試合するかがランダムに決まると考え、広告を打たなかった場合の売上という反実仮想を推定することで、セレクションバイアスなく広告による映画の売上げ増の効果を推定することができます。
操作変数法(二段階最小二乗法)
![]()
一般的に広告費をどれだけ支払うかの意思決定をしている人は売上に影響を与えるような変数を考慮して、広告費を決めていると考えられます。しかしながら、それが分析者のモデルの中で考慮されず、誤差項として扱われてしまうことがあります。そのような状況下で適切な広告効果を推定する方法として操作変数法があります。再び釈迦に説法ですが、操作変数は広告費を通してのみ売上に影響を与える変数のことを指します。ここで、スーパーボウルの話に戻すと、プレイオフなどでのホームチームの勝利はそのスタジアムでの広告費の増加につながると考えられます。しかしながら、プレイオフに行けるかどうかは映画の売上に影響を与える可能性は低いと考えられます。つまり、プレイオフに進んだかどうかは操作変数として扱うことができそうです。
操作変数法によるbの推定量は以下のようになります。
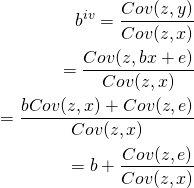
操作変数zと誤差項eが直交することで最後の項は消え、真のパラメータ、つまり真の広告効果を求めることができます。あるいは、以下のような2つの方程式を用いることもできます。
![]()
第1段階ではプレーオフで勝ったかどうかを表すz_cを用いて、2つ目の式のパラメータを推定します。第2段階では第1段階で推定したaを使って予測したx_cを説明変数としてbを推定します。このようなアプローチを字面の通り、二段階最小二乗法と呼びます。この推定結果は操作変数法と等しくなります。
回帰分断デザイン(Regression discontinuity)
閾値を超えることによる因果効果に関心があるケースです。閾値よりも低いもの、高いものの両サイドに近いものを比較する。例えば、学校のクラスで40名のクラスと41名のクラスがいたとして、教育パフォーマンスのクラスの大きさによる因果効果を検証したい場合や、住宅周辺のブロードバンドのスピードが閾値を超えたと閾値を下回るエリアから、ブロードバンドの速度が住宅価格に与える因果効果を検証したい場合などに用いられるます。学校のクラスで40名クラスや41名クラスに配属されるというのはランダムに近いと考えます。
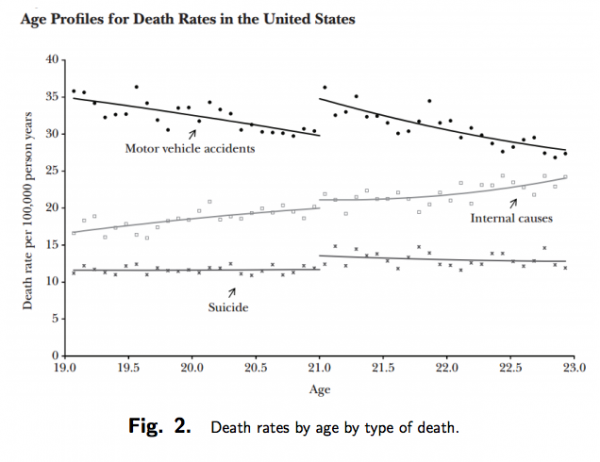
(ペーパーの図を引用しております。この図では21歳前後かどうかという歳のわずかな違いにおいてランダムに近い、処置群とコントロール群が生成されていると考えます。)
Webマーケティングの現場での活用においては、特定のページの閲覧数がある閾値を超えた場合に、そのユーザーに対して特別に処置(例えばクーポンを配る)を行うケースにおいて、閾値を超えたか超えなかったかの比較から処置の因果効果を推定することになります。つまりWebページの閲覧数が閾値を超える超えないはランダムに近いとしています。その際、閾値を超えたものの処置をしそこねた(クーポンを配り損ねた)というのがWeb広告における反実仮想となります。
バリアンのペーパーによると、Google、Microsoft、Facebookのエンジニアはこれらの実装を行い、閾値による比較を行っているようです。
Difference in differences(DID)
Difference in differences(DID)は時系列データでの因果推論において役に立つ手法です。
ここでは介入が仮になかったとしたら、処置群とコントロール群の前後の差は等しいという、以下のような仮定を置きます。
![]()
y_TFは処置群が、介入を受けなかった場合の後の結果(つまり反実仮想)、y_TBは処置群が介入を受ける前の結果、y_CAはコントロール群の後の結果、y_CBはコントロール群の前の結果を表しています。
これを処置群の後の結果y_TAから差し引くと以下のようになります。
![]()
つまり、処置群の前後の差は、処置群とコントロール群の前後の差が等しいのであれば、処置群の前後の差からコントロール群の前後の差を差し引いたもので表現することができます。これがDifference in differencesです。変動を見たい場合はブートストラップ法を適用することで変動幅を求めることができます。
水準のみならず、前後の比に関しても同様に扱うことができ、その場合は以下のように対数の差となります。
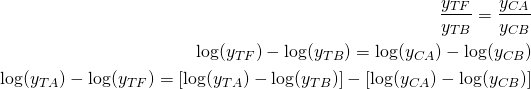
また、DIDにおいては反実仮想を推定する方法として回帰モデルが用いられることがあります。例えば、線形回帰やランダムフォレスト回帰などです。アプローチとしては機械学習に近く、共変量(その日の天気、ニュースなどのイベント、その他の外生変数)を用いてコントロール群の一部のデータで訓練します。続いて、残りのコントロール群のデータを用いてテストをし、モデルとしての汎化性能を高めます。そのモデルを用いて、介入期間における反実仮想を予測し、その反実仮想と実績を比較することで因果効果をもとめます。
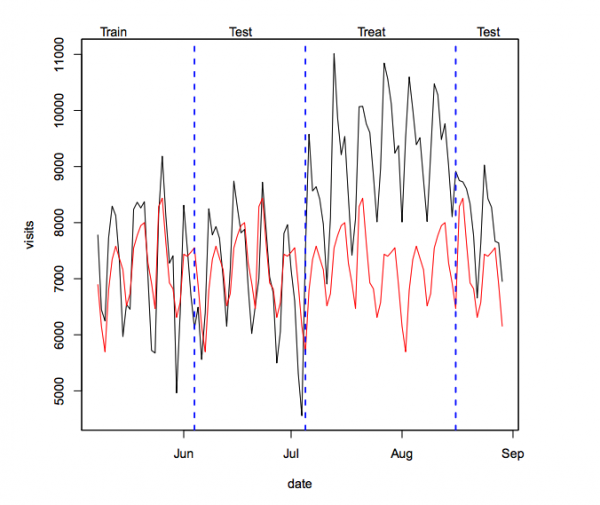
(ペーパーの図を引用しております。こちらでは訓練データを用いて推定したモデルでテスト期間を予測し、介入期間での反実仮想を予測により求め、介入後の実績値と比較しています。)
おわりに
因果推論に関して既に様々な文献がありますが、バリアンの説明が一番頭に入ってきやすかった気がします。もちろん、因果推論のすべてのアプローチが網羅されているわけではないですが、これから因果推論の勉強を頑張ろうというモチベーションを上げるための教材としては良いなと思いました。
参考文献
[1] Varian(2016), “Causal Inference in Economics and Marketing”, PNAS
[2] “回帰不連続デザインRegression discontinuity design(および分割時系列デザイン)”
[3] 岩波データサイエンス刊行委員会(2016), 『岩波データサイエンス Vol.3』