今回は特に目新しい手法というわけでもなく、線形回帰モデルのギブスサンプリングについて忘備録として残しておきたいと思います。
ベイジアン線形回帰モデルはプログラミング言語で言う、Hello World!的なものなので、あえてブログで取り上げる必要があると考えていないのですが、導出をしては忘れの繰り返しが嫌なので自分のために残しておこうと考えました。加えて、Stanのありがたみを感じられ、Stanへのコミットメントが増すのではないかとも期待しています。
・モデル
・数式の展開
・Rのコードの紹介
・おわりに
・参考情報
モデル
東北大学の照井教授の『ベイズモデリングによるマーケティング分析』に載せられている表記に従い、以下のように記します。
説明変数の数がk個の正規線形モデル
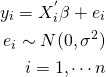
を考える。その場合、尤度関数は
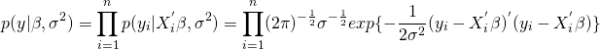
となる。
係数パラメータの事前分布や条件付きの誤差分散の事前分布は以下のように設定する。(βは正規分布に従い、σ2|βは逆ガンマ分布に従う。)
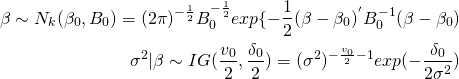
数式の展開
私が大学院生だった時に、数式の展開をどう進めるかを手っ取り早く知る方法としては、「ネットに上がっている海外の大学院の講義資料を漁る」という作戦を取っていました。こうすることで数学のセンスがそれほど高くなくても、理解し進めることができました。今回に関してもおそらく、わかりやすく解説している海外の研究者がいるはずだと思い漁ってみたところ、コロンビア大学の機械学習の講義資料を見つけることができました。
資料はこちらのPDF(Course Notes for Bayesian Models for Machine Learning)で126ページにもなっていますが、導出のステップなどが非常に丁寧に書かれています。

それでは、今回の講義ノートを参考にしながら、線形モデルにおいて、ギブスサンプリングを行うところまでの導出を行いたいと思います。
まず、同時事後分布を以下の左辺のように置き、ベイズの定理を用いて右辺のように表記する。
![]()
次に、条件付き確率の定義と先程の尤度関数から以下のようになる。
![]()
yが与えられたもとでのp(y)は一定のため、比例している分子だけを残すと以下のようになる。
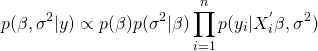
同時事後分布に事前分布の関数を代入していくと、
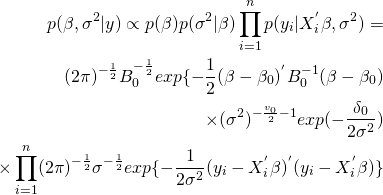
となる。両辺について対数を取ると、
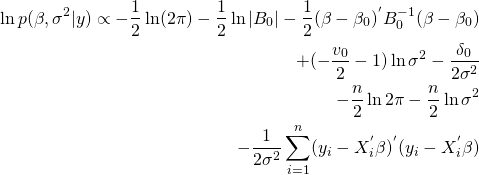
となる。ここでβやσ2についての事前分布の形状から、同時事後分布におけるβやσ2について整理するための目標となる形状を確かめる。
まず、βはp(β)の定義より、対数を取りβについて整理すると、
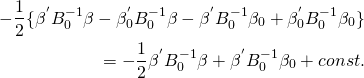
となる。つまり、1/B0や1/B0・β0に該当する表現を先程の対数を取った同時事後分布から得ることを目標とする。
他方、σ2についても同様に、p(β|σ2)の定義より対数を取りσ2について整理すると、
![]()
となる。つまり、ν0やδ0に該当する表現を、同じく対数を取った同時事後分布から得ることを目標とする。
以上のパラメータごとの目標とする形状になるように各々のパラメータについて、対数を取った同時事後分布を整理する。
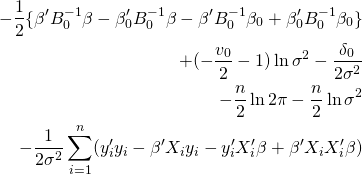
まずはβについてまとめ、関係のない項をconst.にする。
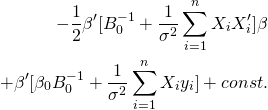
先程もとめた目標の形状を当てはめると以下のようになる。
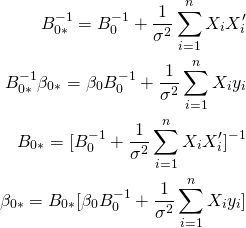
よって、βの事後分布は以下のようになる。
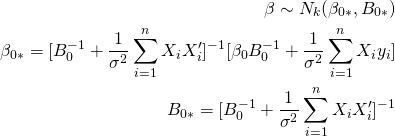
他方、σ2についても同様に、関係のない項をconst.にし、目標の形状にまとめると以下のようになる。
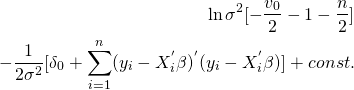
目標の形状と比較すると以下のようになる。
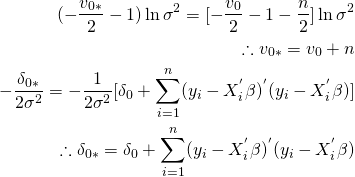
よって、σ2の事後分布は以下のようになる。
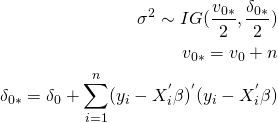
Rのコードの紹介
条件付き事後分布からβやσ2の従う分布の形状がわかったので、それらを使ってRでギブスサンプリングを行います。先日、たまたま見つけた線形回帰モデルのギブスサンプリングのRのソースコードを拝借しようと思います。
ギブスサンプリングでは、先程導出した条件付き分布からβ→σ2と交互にサンプリングしていきます。それを記述したRコードは以下の通りです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
# function for blocked gibbs sampler block_gibbs <- function(y, x, iter, burnin, trim){ # initialize gibbs xprimex_inv <- solve(t(x)%*%x) # calculate once for repeated use in sampler s <- numeric(iter) # shell for phi b <- matrix(nrow=iter, ncol = 4) # shell for betas s[1] <- 6 # initial phi value to start sampler # phi hyperparameters a <- .5 g <- 10000 # gibbs sampling for(i in 2:iter ){ b[i,] <- rmvnorm(n = 1, mean = ((xprimex_inv%*%t(x))%*%y), sigma = s[i-1]*xprimex_inv ) s[i] <- rinvgamma(n = 1, shape = (n/2 + a), rate = .5*( t((y - x%*%t(t(b[i,])) ))%*%(y - x%*%t(t(b[i,])) ) ) + g) } # apply burnin and trimming keep_draws <- seq(burnin,iter,trim) s <- s[keep_draws] b <- b[keep_draws,] # format and output joint_post<-data.frame(b=b,s=s) colnames(joint_post)[1:(ncol(x))]<-paste0('B',0:(ncol(x)-1) ) joint_post_long<-gather(joint_post,keep_draws) %>% rename(param=keep_draws, draw=value) %>% mutate(iter=rep(keep_draws,ncol(joint_post))) return(joint_post_long) } |
先程導出したβの事後分布である正規分布からのサンプリングの後(15~17行目)、そのサンプリングしたβを用いて、同じく先程導出したσ2の事後分布である逆ガンマ分布からサンプリングし(19~21行目)、それを指定した回数だけ繰り返し、所定の数まではバーンインとして除外します。(25~27行目)こうして導出した数式と、ギブスサンプリングのコードを見比べると理解が捗ると思いました。
実際に、先程のGitHubのソースコードを回してみると、以下のようにギブスサンプリングのイタレーションのプロットや、パラメータの事後分布を確認できます。
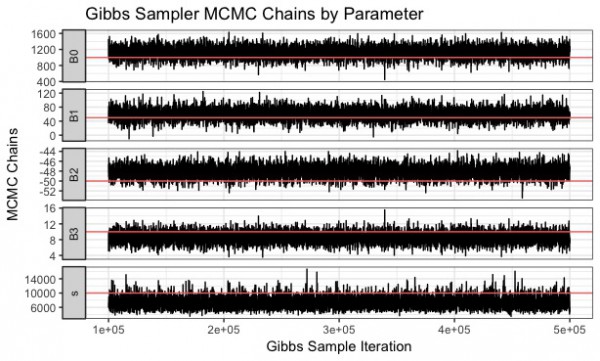
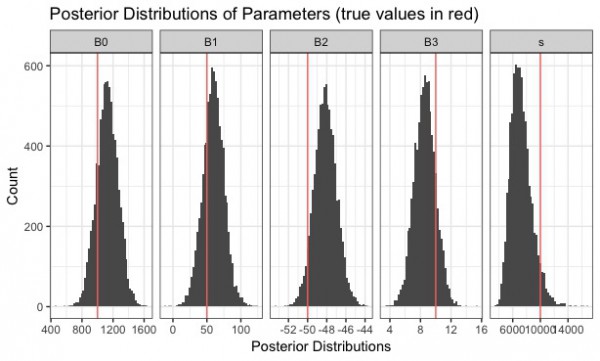
全体のコードはこちらです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 |
################################################################################ ###### 0 - Packages and Simulate Data ################################################################################ library(mvtnorm) library(invgamma) library(ggplot2) library(dplyr) library(tidyr) library(xtable) set.seed(200) n <- 50 # number of observation # simulate model matrix x <- cbind(1, rnorm(n, 0, 1), rnorm(n, 5,10),rnorm(n, 100,10)) # true beta coefficients tb <- c(1000, 50, -50, 10) # true phi ts <- 10000 I <- diag(1,n,n) # identity matrix used for covariance matrix # simulate outcome for regression y <- t(rmvnorm(1, x%*%tb, ts*I)) # simulate many outcomes...used later for asymptotic evaluations y_list <- replicate(1000, t(rmvnorm(1, x%*%tb, ts*I)),simplify = FALSE) ################################################################################ ###### 1 - Run Blocked Gibbs Sampler ################################################################################ # function for blocked gibbs sampler block_gibbs <- function(y, x, iter, burnin, trim){ # initialize gibbs xprimex_inv <- solve(t(x)%*%x) # calculate once for repeated use in sampler s <- numeric(iter) # shell for phi b <- matrix(nrow=iter, ncol = 4) # shell for betas s[1] <- 6 # initial phi value to start sampler # phi hyperparameters a <- .5 g <- 10000 # gibbs sampling for(i in 2:iter ){ b[i,] <- rmvnorm(n = 1, mean = ((xprimex_inv%*%t(x))%*%y), sigma = s[i-1]*xprimex_inv ) s[i] <- rinvgamma(n = 1, shape = (n/2 + a), rate = .5*( t((y - x%*%t(t(b[i,])) ))%*%(y - x%*%t(t(b[i,])) ) ) + g) } # apply burnin and trimming keep_draws <- seq(burnin,iter,trim) s <- s[keep_draws] b <- b[keep_draws,] # format and output joint_post<-data.frame(b=b,s=s) colnames(joint_post)[1:(ncol(x))]<-paste0('B',0:(ncol(x)-1) ) joint_post_long<-gather(joint_post,keep_draws) %>% rename(param=keep_draws, draw=value) %>% mutate(iter=rep(keep_draws,ncol(joint_post))) return(joint_post_long) } # run gibbs sampler with specified parameters post_dist <- block_gibbs(y = y, x = x, iter = 500000, burnin = 100000, trim = 50) ################################################################################ ###### 2 - Summarize and Visualize Posterior Distributions ################################################################################ # calculate posterior summary statistics (stats not used in rest of code) post_sum_stats<-post_dist %>% group_by(param) %>% summarise(median=median(draw), lwr=quantile(draw,.025), upr=quantile(draw,.975)) %>% mutate(true_vals=c(tb,ts)) # merge on summary statistics post_dist <- post_dist %>% left_join(post_sum_stats, by='param') # plot MCMC Chains ggplot(post_dist,aes(x=iter,y=draw)) + geom_line() + geom_hline(aes(yintercept=true_vals, col='red'), show.legend=FALSE)+ facet_grid(param ~ .,scale='free_y',switch = 'y') + theme_bw() + xlab('Gibbs Sample Iteration') + ylab('MCMC Chains') + ggtitle('Gibbs Sampler MCMC Chains by Parameter') # plot Posterior Distributions ggplot(post_dist,aes(x=draw)) + geom_histogram(aes(x=draw),bins=50) + geom_vline(aes(xintercept = true_vals,col='red'), show.legend = FALSE) + facet_grid(. ~ param, scale='free_x',switch = 'y') + theme_bw() + xlab('Posterior Distributions') + ylab('Count') + ggtitle('Posterior Distributions of Parameters (true values in red)') |
おわりに
シンプルなモデルですらこれだけ導出に手間がかかるということからも、Stanなどの確率的プログラミング言語のありがたみは非常に大きいなと思いました。こうして残すことで今後忘れたとしてもすぐに思い出せる気がします。
しかしながら、Stanでは事前分布と尤度を指定してしまえば、事後分布を計算し、知りたいパラメータについて解いた条件付き分布からサンプリングしてくれるわけですから、研究者の寿命を伸ばしたと言っても過言ではないかもしれません。
参考情報
[1]John Paisley (2016), “Course Notes for Bayesian Models for Machine Learning”, Columbia University
[2]照井伸彦 (2008), 『ベイズモデリングによるマーケティング分析』, 東京電機大学出版局
[3]須山敦志 (2017), 『機械学習スタートアップシリーズ ベイズ推論による機械学習入門』, 講談社
[4]stablemarkets,BayesianTutorials/MultipleLinearReg/multiplelinearreg.r