はじめに
仕事で生存時間分析を使うことは結構あるのですが、マーケティングの良いデータセットがない印象でブログにしにくいと感じていました。また、Stanでの生存時間分析の事例もあまり把握していません。そこで使えそうなデータセットやStanのコードを探して、そのデータに対して生存時間分析を適用してみたいと思います。
目次
・生存時間分析とは
・生存時間分析で使えるデータ
・生存時間分析をマーケティングで使う際の用途
・先行研究
・生存時間分析で使えるデータセット
・Stanでの実行例
・おわりに
・参考文献
生存時間分析とは
生存時間分析は、ある時点から興味のあるイベント(マーケティングだと解約など)が発生するまでの期間を分析対象としています。データを手に入れた時点で、すでに解約して、真の累積の契約期間が判明している人と、解約しておらず今後いつ解約するかわからない中での累積の契約期間が残されている人のようなデータを扱うことが多いです。ここでの後者をcensoring(打ち切り)されたデータと呼びます。
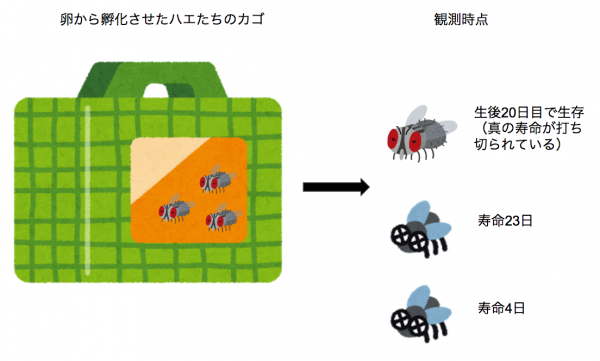
生存時間分析をマーケティングで使う際の用途
ブログなどを読み漁る限り、以下の用途で生存時間分析を活用できるようです。
- 顧客のサービス離脱率の予測、離脱原因の特定
- 顧客がマーケティングキャンペーンに反応するまでの期間の長さ
- 故障率の予測、故障原因の特定
先行研究
Stanを用いた分析事例は、調べた限りですが以下のモデルがあるようです。
- 指数分布のモデル
- Weibull(ワイブル)分布による比例ハザードモデル
- ハザードの対数値についてのランダムウォークモデル
- 2階差分のマルコフ場モデル(生存時間の確率分布は正規分布)
- 1階差分のランダムウォークモデル(生存時間の確率分布は正規分布)
生存時間分析で使えるデータセット
事例を調べる過程で見つけた、生存時間分析に適したデータセットは以下の通りです。
- RのMASSパッケージに含まれているgehan
- Rのsurvivalパッケージに含まれているleukemia(白血病)
- Rのsurvivalパッケージに含まれているveteran
- Pythonのlifelineパッケージに含まれているrossi(逮捕された人が再逮捕されるまでの期間と共変量)
- kaggleで提供されているEmployee Attrition Can you forecast employee attrition?のデータセット
- Princeton Divorce Studyのデータ
- IBMが提供している、Using Customer Behavior Data to Improve Customer Retentionという電話会社の解約に関すCRMデータ
どうやら、マーケティング、HR、離婚、再犯と幅広いデータがオープンソースで手に入るようです。
Stanでの実行例
今回は、「Using Customer Behavior Data to Improve Customer Retention」のデータセットを用いて、先行研究のソースコードにより生存時間分析をしてみようと思います。データは電話会社の顧客の解約に関するもので、様々な顧客の履歴データなどが用意されています。
先行研究のソースコードはWeibull分布を想定した比例ハザードモデルです。今回は決済の電子化の有無と離脱の関係を確かめてみます。なお、今回の打ち切りデータは契約期間となります。
まずはStanのコードはこちらです。Xobs_bgに説明変数が来るようにデータを用意しておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 |
functions { vector sqrt_vec(vector x) { vector[dims(x)[1]] res; for (m in 1:dims(x)[1]){ res[m] = sqrt(x[m]); } return res; } vector bg_prior_lp(real r_global, vector r_local) { r_global ~ normal(0.0, 10.0); r_local ~ inv_chi_square(1.0); return r_global * sqrt_vec(r_local); } } data { int<lower=0> Nobs; int<lower=0> Ncen; int<lower=0> M_bg; vector[Nobs] yobs; vector[Ncen] ycen; matrix[Nobs, M_bg] Xobs_bg; matrix[Ncen, M_bg] Xcen_bg; } transformed data { real<lower=0> tau_mu; real<lower=0> tau_al; tau_mu = 30.0; tau_al = 30.0; } parameters { real<lower=0> tau_s_bg_raw; vector<lower=0>[M_bg] tau_bg_raw; real alpha_raw; vector[M_bg] beta_bg_raw; real mu; } transformed parameters { vector[M_bg] beta_bg; real alpha; beta_bg = bg_prior_lp(tau_s_bg_raw, tau_bg_raw) .* beta_bg_raw; alpha = exp(tau_al * alpha_raw); } model { yobs ~ weibull(alpha, exp(-(mu + Xobs_bg * beta_bg)/alpha)); target += weibull_lccdf(ycen | alpha, exp(-(mu + Xcen_bg * beta_bg)/alpha)); beta_bg_raw ~ normal(0.0, 1.0); alpha_raw ~ normal(0.0, 1.0); mu ~ normal(0.0, tau_mu); } generated quantities { real yhat_uncens[Nobs + Ncen]; real log_lik[Nobs + Ncen]; real lp[Nobs + Ncen]; for (i in 1:Nobs) { lp[i] = mu + Xobs_bg[i,] * beta_bg; yhat_uncens[i] = weibull_rng(alpha, exp(-(mu + Xobs_bg[i,] * beta_bg)/alpha)); log_lik[i] = weibull_lpdf(yobs[i] | alpha, exp(-(mu + Xobs_bg[i,] * beta_bg)/alpha)); } for (i in 1:Ncen) { lp[Nobs + i] = mu + Xcen_bg[i,] * beta_bg; yhat_uncens[Nobs + i] = weibull_rng(alpha, exp(-(mu + Xcen_bg[i,] * beta_bg)/alpha)); log_lik[Nobs + i] = weibull_lccdf(ycen[i] | alpha, exp(-(mu + Xcen_bg[i,] * beta_bg)/alpha)); } } |
続いて、このStanコードをキックするためのRのソースコードです。 元のデータが7043件と多すぎるのでランダムサンプリングしています。サンプリング数を8000、チェイン数を4にして実行します。(なお、可視化のソースコードもあるので結構長くなっていますので。頑張ってスクロールしてください。)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 |
library(tidyverse) library(rstan) rstan_options(auto_write = TRUE) options(mc.cores = parallel::detectCores()) # Data Import ------------------------------------------------------------- dataset <- read_csv("dataset/WA_Fn-UseC_-Telco-Customer-Churn.csv") dataset$Churn <- as.factor(dataset$Churn) dataset$censored <- if_else(dataset$Churn == "Yes", 0, 1) dataset_obs <- sample_n(dataset %>% filter(censored == 0), 300) dataset_cens <- sample_n(dataset %>% filter(censored == 1), 75) dataset <- rbind(dataset_cens, dataset_obs) # Kick Stan Code ---------------------------------------------------------- stan_data <- list( ## 離脱のイベントが計測された顧客 Nobs = sum(dataset$censored == 0), ## 途中で打ち切られた顧客 Ncen = sum(dataset$censored == 1), ## 共変量の数 M_bg = 1, ## 離脱イベントが計測された顧客の契約期間 yobs = dataset$tenure[dataset$censored == 0], ## 途中で打ち切られた顧客の契約期間 ycen = dataset$tenure[dataset$censored == 1], ## 離脱のイベントが計測された顧客の共変量 Xobs_bg = matrix(as.numeric(dataset$PaperlessBilling == "Yes")[dataset$censored == 0]), ## 途中で打ち切られた顧客の共変量 Xcen_bg = matrix(as.numeric(dataset$PaperlessBilling == "Yes")[dataset$censored == 1]) ) fit <- rstan::stan(file = "model/weibull_fit.stan", data = stan_data, iter = 8000, chains = 4, seed = 1234, control = list(max_treedepth = 15,adapt_delta=0.99) ) # diagnose ---------------------------------------------------------------- fit summary_table <- data.frame(summary(fit)$summary) ggplot(data = data.frame(Rhat = summary_table$Rhat), aes(Rhat)) + geom_histogram() rstan::traceplot(fit, par = c("alpha","mu","beta_bg")) bayesplot::mcmc_acf(as.matrix(fit), pars = c("alpha","mu","beta_bg[1]")) bayesplot::mcmc_areas(as.matrix(fit), pars = c("alpha","mu","beta_bg[1]"), prob = 0.95) # visualization ---------------------------------------------------------------- draws <- tidybayes::tidy_draws(fit) draws treatment_assignment <- c(as.numeric(dataset$PaperlessBilling == "Yes")[dataset$censored == 0], as.numeric(dataset$PaperlessBilling == "Yes")[dataset$censored == 1]) treatment_assignment_df <- data_frame(obs = 1:nrow(dataset),treatment = treatment_assignment) treatment_assignment_df draws_yhat_uncens <- draws %>% select(.chain, .iteration, .draw, starts_with("yhat_uncens")) %>% gather(key = key, value = yhat_uncens, starts_with("yhat_uncens")) %>% separate(col = key, sep = "uncens", into = c("key","obs")) %>% select(-key) %>% ## Avoid using regular expressions with square brackets (syntax highlighter broke). ## https://stringr.tidyverse.org/articles/stringr.html mutate(obs = as.integer(str_sub(obs, 2, -2))) %>% left_join(y = treatment_assignment_df) draws_yhat_uncens ggplot(data = draws_yhat_uncens, mapping = aes(x = yhat_uncens, color = factor(treatment))) + geom_density(n = 512*10) + coord_cartesian(xlim = c(0,160)) + theme_bw() + theme(axis.text.x = element_text(angle = 90, vjust = 0.5), legend.key = element_blank(), plot.title = element_text(hjust = 0.5), strip.background = element_blank()) ## Constructor for treatment-specific survival function construct_survival_function <- function(alpha, mu, beta, x) { function(t) { sigma_i <- exp(-1 * (mu + beta * x) / alpha) exp(- (t / sigma_i)^alpha) } } ## Random functions survival_functins <- draws %>% select(.chain, .iteration, .draw, alpha, mu, `beta_bg[1]`) %>% ## Simplify name rename(beta = `beta_bg[1]`) %>% ## Construct realization of random functions mutate(`S(t|1)` = pmap(list(alpha, mu, beta), function(a,m,b) {construct_survival_function(a,m,b,1)}), `S(t|0)` = pmap(list(alpha, mu, beta), function(a,m,b) {construct_survival_function(a,m,b,0)})) survival_functins times <- seq(from = 0, to = 160, by = 0.1) times_df <- data_frame(t = times) ## Try first realizations survival_functins$`S(t|1)`[[1]](times[1:10]) survival_functins$`S(t|0)`[[1]](times[1:10]) ## Apply all realizations survival <- survival_functins %>% mutate(times_df = list(times_df)) %>% mutate(times_df = pmap(list(times_df, `S(t|1)`, `S(t|0)`), function(df, s1, s0) {df %>% mutate(s1 = s1(t), s0 = s0(t))})) %>% select(-`S(t|1)`, -`S(t|0)`) %>% unnest() %>% gather(key = treatment, value = survival, s1, s0) %>% mutate(treatment = factor(treatment, levels = c("s1","s0"), labels = c("Yes","No"))) ## Average on survival scale survival_mean <- survival %>% group_by(treatment, t) %>% summarize(survival_mean = mean(survival), survival_95upper = quantile(survival, probs = 0.975), survival_95lower = quantile(survival, probs = 0.025)) ggplot(data = survival, mapping = aes(x = t, y = survival, color = treatment, group = interaction(.chain,.draw,treatment))) + geom_line(size = 0.1, alpha = 0.02) + geom_line(data = survival_mean, mapping = aes(y = survival_mean, group = treatment)) + geom_line(data = survival_mean, mapping = aes(y = survival_95upper, group = treatment), linetype = "dotted") + geom_line(data = survival_mean, mapping = aes(y = survival_95lower, group = treatment), linetype = "dotted") + facet_grid(. ~ treatment) + theme_bw() + theme(axis.text.x = element_text(angle = 90, vjust = 0.5), legend.key = element_blank(), plot.title = element_text(hjust = 0.5), strip.background = element_blank()) ## Average on parameter space average_parameters <- draws %>% summarize(alpha = mean(alpha), mu = mean(mu), beta = mean(`beta_bg[1]`)) average_parameters average_params_survival1 <- with(average_parameters, construct_survival_function(alpha, mu, beta, 1)) average_params_survival0 <- with(average_parameters, construct_survival_function(alpha, mu, beta, 0)) average_params_survival <- data_frame(t = seq(from = 0, to = 160, by = 0.1), s1 = average_params_survival1(t), s0 = average_params_survival0(t)) %>% gather(key = treatment, value = survival, -t) %>% mutate(treatment = factor(treatment, levels = c("s1","s0"), labels = c("Yes","No"))) average_params_survival %>% ggplot(mapping = aes(x = t, y = survival, color = treatment, group = treatment)) + geom_line() + theme_bw() + theme(axis.text.x = element_text(angle = 90, vjust = 0.5), legend.key = element_blank(), plot.title = element_text(hjust = 0.5), strip.background = element_blank()) ggplot(data = survival, mapping = aes(x = t, y = survival, color = treatment, group = interaction(.chain,.draw,treatment))) + geom_line(size = 0.1, alpha = 0.02) + geom_line(data = survival_mean, mapping = aes(y = survival_mean, group = treatment)) + geom_line(data = average_params_survival, mapping = aes(group = treatment), linetype = "dotted") + facet_grid(. ~ treatment) + theme_bw() + theme(axis.text.x = element_text(angle = 90, vjust = 0.5), legend.key = element_blank(), plot.title = element_text(hjust = 0.5), strip.background = element_blank()) |
Rhatは全て1.05以下になっています。
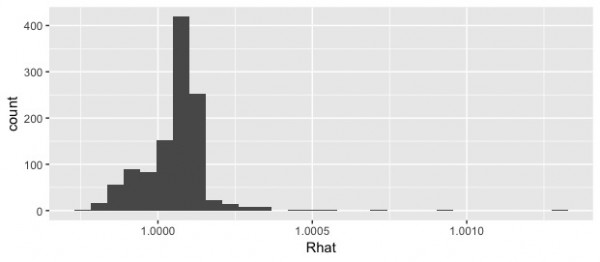
traceplotを見る限り、重なり合っているので問題なさそうです。
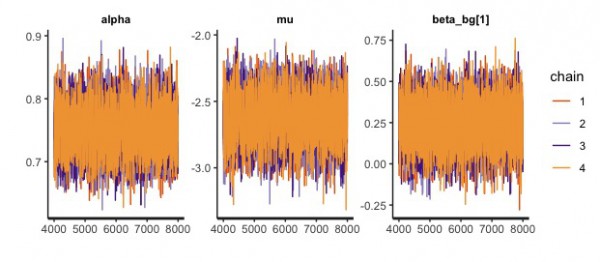
各パラメータごとの自己相関係数です。こちらも問題なさそうです。

推定したパラメータの分布です。
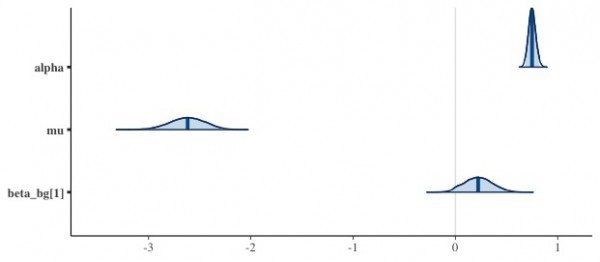
横軸は推定した継続期間です。決済の電子化をしていない消費者は、契約期間の短い際の確率密度が低い傾向があるようです。
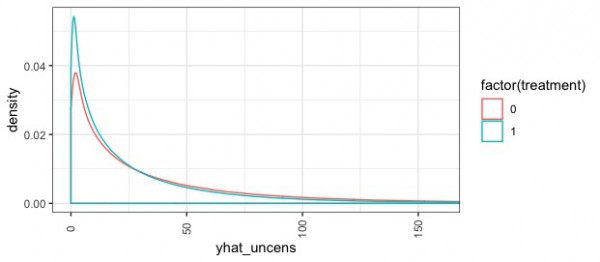
どうやら離脱率に関して決済の電子化をしていない消費者は、そうでない消費者よりも低いようです。
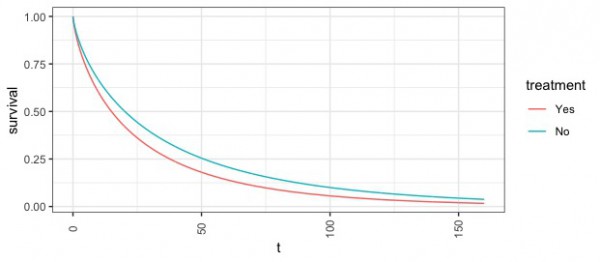
こちらは95%で取りうる範囲をそれぞれプロットしたものです。
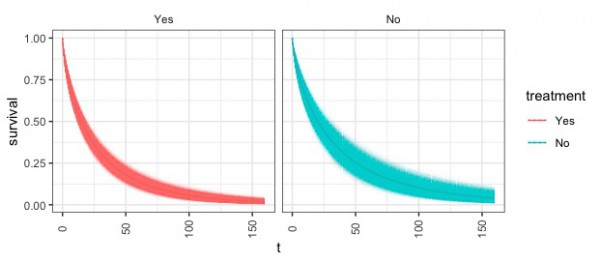
おわりに
Stanで生存時間分析を行うという事例はそんなに多くはないものの、業界の長たちが良いコードを作成してくれていました。また、面白そうなデータセットも見つけることができました。このようなデータがもっと広まっていけば、マーケティングにおける生存時間分析がより活発に行われるのかもしれません。
参考文献
[1] 豊田秀樹 (2017) 『実践 ベイズモデリング -解析技法と認知モデル-』 朝倉書店
[2]生存時間解析入門
[3]比例ハザードモデルはとってもtricky!
[4]Stanで生存時間解析(Weibull 回帰)
[5]生存時間分析をStanで実行してみた
[6]階層ベイズ生存解析を用いたwebサイトの訪問者分析に関するStanでの実装
[7]生存時間分析 – ハザード関数に時間相関の制約を入れる
[8]Bayesian Survival Analysis 1: Weibull Model with Stan
[9]Bayesian Inference With Stan ~062~
[10]生存時間解析について – 概要編
[11]Survival Analysis for Employee Attrition ※kaggleで提供されているHR系のデータをサバイバル分析に用いている。
[12]Survival Analysis with R※Random Forests Modelによる生存時間の推定がなされている。
[13]Survival Analysis with R and Aster ※服役後の犯罪に関する分析や、離婚の分析などをしている。
[14]Survival Analysis of Mobile Prepaid Customers Using the Weibull Distribution(ダウンロード注意)