はじめに
stanのユーザーガイドを見ていて、項目反応理論(IRT)についての章があり気になりました。勉強会のLTなどで手法の名前をちらっと聞いたことはあったのですが、使い道について調べていませんでした。ビジネスにおける実活用もしやすそうだと思ったので、カジュアルに分析して備忘録として残したいと思います。
目次
・項目反応理論(Item Response Theory:IRT)とは
・ビジネスでの適用可能性について
・データ
・モデルの推定
・結果の解釈
・おわりに
項目反応理論(Item Response Theory:IRT)とは
関西学院大学の教授のブログによると、
項目反応理論とは、テストについての計量モデルで、問題に対する正解・不正解のデータから、問題の特性や、回答者の学力を推定するためのモデルです。
とあります。また、Wikipediaによると、TOEFLの問題の評価のために使われているそうです。
主に、バイナリーと順序変数のモデルがあるようで、以下の母数がモデルに想定されています。どちらもほぼ同じです。
回答が2値変数のモデル
- 2母数のロジスティックモデル
- 特性値(例えば、広告配信の満足度とか)
- 識別度母数(項目特性曲線の傾き)
- 困難度母数(項目特性曲線の切片)
- 定数
回答が順序変数のモデル(まずい < まぁまぁ < おいしい)
- 段階反応モデル
- 特性値(例えば、広告配信の満足度とか)
- 識別度母数(項目特性曲線の傾き)
- 困難度母数(項目特性曲線の切片)
※項目特性曲線は横軸に特性値、縦軸に質問の正答率を取ったものです。
ビジネスでの適用可能性について
- 顧客のアンケート結果の解釈
- 異質な集団間の得点を比較可能
- 異なる尺度間の得点を比較可能(昔のアンケートだと5段階、今のアンケートは7段階などの状況はビジネスデータでありうる。)
- 人事評価のバイアスの統制
- 採用面接時の個人特性の正当な評価
- アンケート項目の項目削減によるアンケートコストの低減
- 各アンケート項目が理解されたかどうかを分析し、一つ一つのアンケート項目の精度を高める
データ
今回扱うデータはbaysemパッケージに入っているデータセットです。Yellow Pagesの広告プロダクトにおける満足度サーベイの回答データで、全ての回答は1から10のスケールで点数が付けられています(1がPoorで10がExcellent)。質問数は10個で、回答数は1811件です。
各質問の内容(baysemパッケージのドキュメントに載っていました。)
q1:全体の満足度
価格について
q2:競争的な価格設定
q3:昨年と同じ広告の最小値に対しての価格の引き上げ
q4:消費者の数に対しての適切な価格設定
効果について
q5:広告の購入の潜在的な影響
q6:広告を通じて自身のビジネスへの集客ができたか
q7:多くの消費者にリーチしたかどうか
q8:年間を通じて消費者に対する長期での露出があったか
q9:多くの家計やビジネスを必要としている人に届いたかどうか
q10:ビジネスを必要としている地理上のエリアに届いたかどうか
今回のIRT適用における特性値は、「広告プロダクトに関する満足度の傾向」としてみたいと思います。
モデルの推定
今回は教科書にならって以下の段階反応モデルを用います。
![]()
ここでaは識別力(広告の満足度が高まりやすいかどうか)、bは境界パラメータ(回答カテゴリ間の境界値)、θは特性(回答者がどれだけ広告に満足しているか)を表しています。Dは定数項で、以下では1とおいています。cはアンケートの回答のカテゴリ番号です。今回の例では10段階の評価が入ることになります。最後に、uは反応を、jは質問の番号を表しています。
こちらの本のサポートサイトからダウンロードできるzipファイルにstanのコードやRコードがありますので、そちらを利用しています。
モデルですが、以下のような設定となっています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
data{ int ni; // the number of record int nj; // the number of item int nc; // the number of grade real D; // Constant int<lower=1,upper=10> y[ni,nj]; // data } parameters{ vector<lower=0,upper=5>[nj] a; ordered[nc-1] ba[nj]; vector<lower=-4,upper=4>[ni] theta; } transformed parameters{ real b[nj,nc]; vector<lower=0,upper=1>[nc-1] pa[ni,nj]; simplex[nc] p[ni,nj]; for (j in 1:nj){ for (c in 1:nc){ if (c ==1){ b[j,c] = ba[j,c]; }else if (c ==nc){ b[j,c] = ba[j,c-1]; }else{ b[j,c] = (ba[j,c-1]+ba[j,c])/2; } } } for (i in 1:ni){ for (j in 1:nj){ for (c in 1:nc-1){ pa[i,j,c] = 1/(1+exp(-D*a[j]*(theta[i] - ba[j,c]))); } } } for (i in 1:ni){ for (j in 1:nj){ for(c in 1:nc){ if (c==1){ p[i,j,c] = 1-pa[i,j,c]; }else if(c==nc){ p[i,j,c] = pa[i,j,c-1]; }else{ p[i,j,c] = pa[i,j,c-1] - pa[i,j,c]; } } } } } model{ for (i in 1:ni){ theta[i] ~ normal(0,1); for (j in 1:nj){ y[i,j] ~ categorical(p[i,j]); } } for (j in 1:nj){ a[j] ~ lognormal(0,sqrt(0.5)); for (c in 1:nc-1){ ba[j,c] ~ normal(0,2); } } } generated quantities{ real bg[nj,nc]; bg = b; } |
こちらをキックするためのRコードです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
library(bayesm) library(rstan) library(shinystan) library(bayesplot) library(tidyverse) library(gridExtra) # Data Import ------------------------------------------------------------- data("customerSat") dataset <- customerSat # Kick Stan model --------------------------------------------------------- ni <- nrow(dataset) # 分析対象者の数 nj <- ncol(dataset) # 項目数 nc <- length(table(as.factor(dataset$q1))) # 回答の種類 D <- 1 # 定数項 stan_data <- list(y = dataset, nj = nj, ni = ni, nc= nc, D = D) par <- c("theta","ba","a","b") war <- 2500 ite <- 5000 see <- 1234 dig <- 2 cha <- 4 fit <- stan(file = "model/graded_response_model.stan", data = stan_data, pars = par, verbose = F, seed = see, chains = cha, warmup = war, iter = ite) # Diagnose ---------------------------------------------------------------- traceplot(fit) print(fit, pars = par, digits_summary = dig) summary_table <- data.frame(summary(fit)$summary) ggplot(data = data.frame(Rhat = summary_table$Rhat), aes(Rhat)) + geom_histogram() |
処理時間としては、2014年末モデルのMacbook Proのcorei5、メモリ8GBで数時間程度でした。(正確な時間はわかりませんが、寝て起きたら計算が終わっていました。)
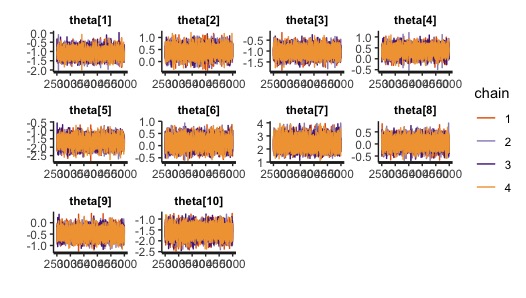
どうやら収束してそうです。
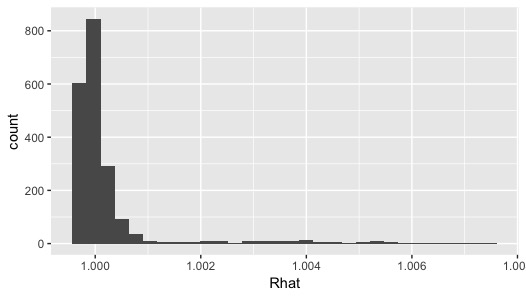
Rhatも1.1未満におさまっています。
結果の解釈
|
1 2 3 |
# histogram of theta theta <- rstan::extract(fit)$theta %>% apply(2,mean) ggplot(data = data.frame(theta_mean = theta), aes(theta_mean)) + geom_histogram() |
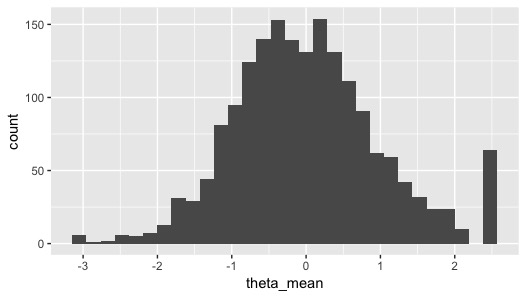
まず、推定した特性値の値のユーザーごとの平均値を求めて、ヒストグラムを描いてみます。どうやら、上限周辺にやたらと高い評価をしてそうなユーザーがいるようです。
最後に、項目特性曲線を質問ごとに、そして回答ごとに描いてみようと思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# Visualization ----------------------------------------------------------- alpha <- rstan::extract(fit)$a %>% apply(2,mean) for (i in 1:nj){ eval(parse(text=paste0("beta_",i," <- rstan::extract(fit)$b[1:10000,",i,",1:nc] %>% apply(2,mean)"))) } for (i in 1:nj){ eval(parse(text=paste0("ggdf_",i," <- data.frame(matrix(ncol = nc,nrow = length(theta))) ; colnames(ggdf_",i,") <- 1:nc"))) } ## probability for(i in 1:nj){ for (j in 1:nc){ eval(parse(text=paste0("ggdf_",j,"[,",i,"] <- 1/(1+exp(-alpha[",i,"]*(theta-beta_",j,"[",i,"])))"))) eval(parse(text=paste0("ggdf_",j,"$theta <- theta"))) } } ## gather for (i in 1:nj){ eval(parse(text=paste0("ggdf_gt_",i," <- ggdf_",i," %>% tidyr::gather(key=var,value,-theta,factor_key=TRUE)"))) } ## ggplot for (i in 1:nj){ eval(parse(text=paste0("p",i," <- ggplot(data = ggdf_gt_",i,", aes(x = theta, y = value, colour = var)) + geom_line() + ggtitle(\"Q",i,"\")"))) } # 2×3でグラフを描画 grid.arrange(p1, p2, p3, p4, p5, nrow = 3) grid.arrange(p6, p7, p8, p9, p10, nrow = 3) |
質問1~10に関して、10段階の回答ごとの項目反応曲線を以下に描いています。上まで戻るのが面倒なので、質問内容を再掲します。
q1:全体の満足度
q2:競争的な価格設定
q3:昨年と同じ広告の最小値に対しての価格の引き上げ
q4:消費者の数に対しての適切な価格設定
q5:広告の購入の潜在的な影響
q6:広告を通じて自身のビジネスへの集客ができたか
q7:多くの消費者にリーチしたかどうか
q8:年間を通じて消費者に対する長期での露出があったか
q9:多くの家計やビジネスを必要としている人に届いたかどうか
q10:ビジネスを必要としている地理上のエリアに届いたかどうか
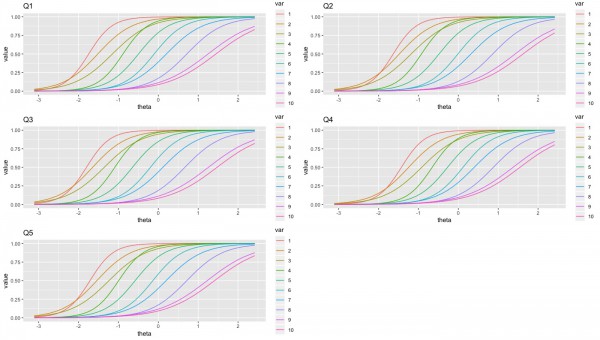
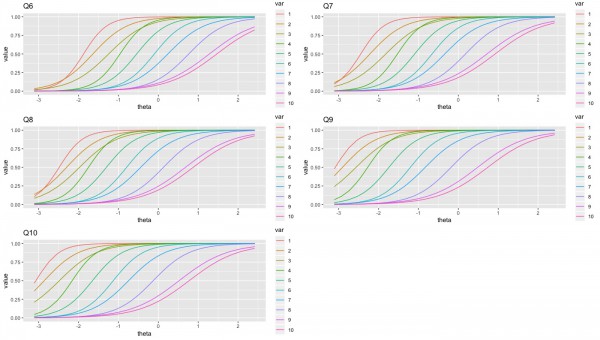
これらの傾向から、9〜10点を獲得するにはある程度は特性値が高まる必要がある質問としては、q1〜q6のように見えます。価格や購買など自身のビジネスに直結しそうな質問が多い印象です。逆にふわっとした質問であるq7~q10は特性値が低くても9〜10点を取れる可能性が高い傾向があります。
おわりに
Stanのユーザーガイドを読むことで、普段自分が業務で扱っているアプローチなどが如何に限定的であることが実感できました。今回はIRTのアンケートデータへの適用事例を知れ、そこから様々な文献や便利なコードに至ることができました。社内のアンケートデータへの適用は面白そうだと思いますので業務で使ってみようと思います。
参考情報
[1] 豊田秀樹 (2017) 『実践 ベイズモデリング -解析技法と認知モデル-』 朝倉書店
[2] Yoshitake Takebayashi (2015) 「項目反応理論による尺度運用」 SlideShare
[3] 持主弓子・今城志保 (2011) 「IRTの組織サーベイへの応用」
[4] 清水裕士 (2017) 「項目反応理論をStanで実行するときのあれこれ」 Sunny side up!
[5] 清水裕士 (2016) 「Stanで多次元項目反応理論」 Sunny side up!
[6] 小杉考司 (2013) 「項目反応理論について」
[7] Daniel C. Furr et al. (2016) “Two-Parameter Logistic Item Response Model”
[8] daiki hojo (2018) “Bayesian Sushistical Modeling” Tokyo.R#70
[9] abrahamcow (2017) 「[RStan]項目反応理論の応用でフリースタイルダンジョン登場ラッパーの強さをランキングしてみた」
