はじめに
私は基本的にデータ分析を生業としていますが、どうしても分析の案件が足りない時期は分析以外のものに手を染めることもあります。主に、RPAやクローリング、APIを用いたソーシャルリスニングなどです。今後も分析以外のことをやる時があるとしたら、レパートリーを増やしたいですよね。なので、ORについて調べてみることにしました。
ORとは
公益社団法人日本オペレーションズ・リサーチ学会による定義によると、
「現象を抽象化した数理モデルを構築し, モデル分析に基づいて種々の問題, とりわけ意思決定問題の解決を支援する方法論や技法の総称. 情報化社会の進展に伴って, 線形計画法に代表される最適化モデルや待ち行列理論に代表される確率的なモデル等, 多様なモデルに基づく分析が, 経営計画や生産・販売・財務等の企業意思決定や都市・公共システム等広く社会一般の問題解決に大きな役割を果たしている.」
とされています。うむ、お硬い感じの定義ですね。
他の記述にわかりやすい表現がありました。
「問題を科学的,つまり「筋のとおった方法」を用いて解決するための「問題解決学」であります」
これならわかりやすいです。
問題解決につながる、あらゆる科学的な手法を扱っているのがORだと考えてよいのだろうと思います。
ORの強みとしては、
- 大規模プロジェクトなどの遂行に役立つ
- 常識や過去の経験では判断が難しい問題に対する解の提供をしてくれる
- 経営、工学、医学、公共政策など幅広い分野での適用可能性がある
などがあげられています。
ORの手法
問題解決につながるなら何でもありということで、手法も幅広いようです。私の持っている参考書やOR学会のサイトの情報から判断すると少なくとも以下の手法が扱われているようです。
・数理最適化
・組合せ最適化
・シミュレーション
・待ち行列
・AHP(階層的意思決定法)
・DEA(包絡分析法)
・スケジューリング
・ゲーム理論
・ネットワーク理論
・データマイニング
データマイニングはもはや機械学習ブームなので特筆したものではないですが、最近データ分析を始めた人などは知らないことも多いのではないでしょうか。
仕事やプライベートでの使い所
- 社員のシフトを決めるタスク
- ミーティングに参加する社員の移動距離が一番少ない、空いている会議室を見つけるタスク
- コンビニのレジを何台おけば客の待ち時間が想定内になるのか
- 工程A、B、Cの全てを経る必要のある作業で、生産ラインを安定させるには今日はAとBとCのどの工程をどれだけすすめるべきか決めるタスク
- 旅行をする際に、予算を所与のもとで、どのスポットに立ち寄ることが効用が高いかを見つけるタスク
Rでの実践例
ようやく、この記事の本題です。Rでオペレーションズリサーチなどという書籍に出会えていないので、Rを用いてオペレーションズリサーチを行っている事例を集めてみようと思います。ブログを漁ればいろいろとありますね。
なお、答え合わせを兼ねて、登場する問題は『Excelで学ぶOR』の例題で表現を変えています。網羅性はないものの、出来るだけ取り上げてみようと思います。
数理最適化
シュークリーム専門店、pseudoカモノハシはシュークリームとパンケーキの生産をしているが、厨房があまりに狭すぎてシュークリームとパンケーキの同時生産ができない。また、労働基準法の観点から厨房の利用時間は40時間以内となる。
シュークリームの生産に関しての情報は以下の通りとします。
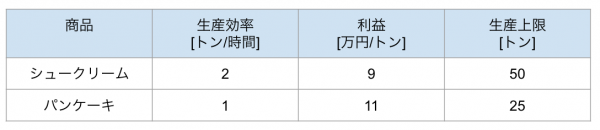
pseudoカモノハシはシュークリームとパンケーキをどれだけ生産すれば利益を最大にすることができるだろうかという問題です。
定式化すると以下のようになります。
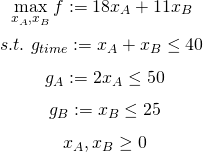
RのlpSolveパッケージを用いてこの線形計画問題を解いてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
library(lpSolve) # 目的関数の係数 f.obj <- c(18, 11) # 制約式の左辺の係数 f.con <- matrix (c(1, 1, 2, 0, 0, 1), ncol=2, byrow=TRUE) # 制約式の等号・不等号 f.dir <- c("<=", "<=", "<=") # 制約式の右辺 f.rhs <- c(40, 50, 25) # 決定変数は非負と仮定されているので,非負条件の記述は不要 # 目的関数の最大値を返す lp ("max", f.obj, f.con, f.dir, f.rhs) #解を求める lp("max", f.obj, f.con, f.dir, f.rhs)$solution |
実行するとこんな結果です。
|
1 2 3 4 5 6 |
> # 目的関数の最大値を返す > lp ("max", f.obj, f.con, f.dir, f.rhs) Success: the objective function is 615 > # 解を求める > lp("max", f.obj, f.con, f.dir, f.rhs)$solution [1] 25 15 |
pseudoカモノハシは25個のシュークリーム、15個のパンケーキを生産することで615万円の売上をあげることができるということになります。
係数がどれくらい変わっても最適解が変化しないのかを知るための感度分析も簡単にできるようです。
係数がちょっと変わっただけで崩れる最適化とかだと実務で使う際に怖いので、大事な工程ですね。
|
1 2 3 4 5 6 7 |
# 感度分析 # 最適解が変化しない目的関数の係数の下限値 lp ("max", f.obj, f.con, f.dir, f.rhs, compute.sens=T)$sens.coef.from # 最適解が変化しない目的関数の係数の上限値 lp ("max", f.obj, f.con, f.dir, f.rhs, compute.sens=T)$sens.coef.to # 最適解が変化しない目的関数の係数の上限値 lp ("max", f.obj, f.con, f.dir, f.rhs, compute.sens=T) |
輸送問題(ネットワーク型の線形計画法)
シュークリーム専門店、pseudoカモノハシは事業拡大につき、3つの食料庫と4つの工房を持つに至った。シュークリームやパンケーキを生産するためには食料庫から工房までトラックで輸送をする必要がある。各々の食料庫から工房までの輸送コストは以下の表の1行1列目〜3行4列目までで表される。食料庫には置ける在庫が決まっており、表の5列目で与えられている。工房には客の注文ベースの生産ノルマが課されており、表の4行目で与えられている。
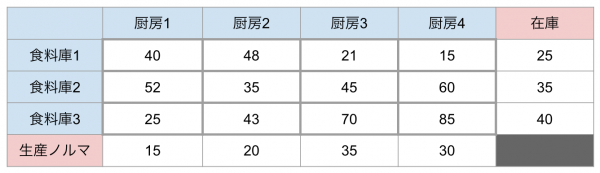
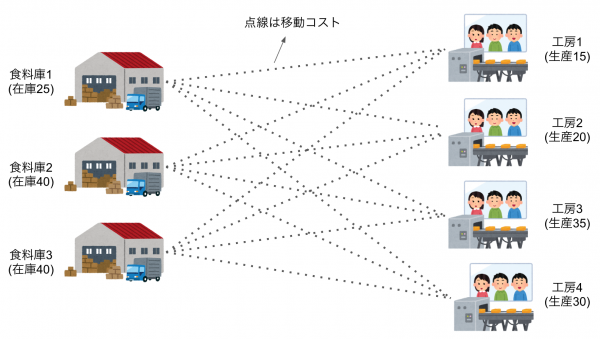
以上、pseudoカモノハシは輸送コストを最も下げて生産するにはどの食料庫からどの工房に材料を輸送すればよいか、と言う問題となります。
定式化すると以下のようになります。
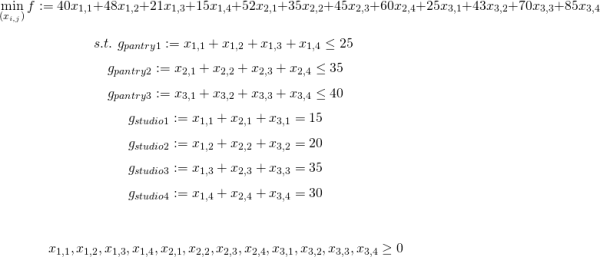
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
library(lpSolve) # 目的関数の係数 f.obj <- c(40, 48, 21, 15, 52, 35, 45, 60, 25, 43, 70, 85) # 制約式の左辺の係数 f.con <- matrix (c(1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0 ,0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1), ncol=12, byrow=TRUE) # 制約式の等号・不等号 f.dir <- c("<=", "<=", "<=", "==", "==", "==", "==") # 制約式の右辺 f.rhs <- c(25, 35, 40, 15, 20, 35, 30) # 決定変数は非負と仮定されているので,非負条件の記述は不要 # 目的関数の最大値を返す lp ("min", f.obj, f.con, f.dir, f.rhs) # 解を求める lp("min", f.obj, f.con, f.dir, f.rhs)$solution |
このコードを実行すると以下のようになり、輸送コストの最小値は3610であることが示されている。
|
1 2 3 4 5 6 |
> # 目的関数の最大値を返す > lp ("min", f.obj, f.con, f.dir, f.rhs) Success: the objective function is 3610 > # 解を求める > lp("min", f.obj, f.con, f.dir, f.rhs)$solution [1] 0 0 0 25 0 0 30 5 15 20 5 0 |
ナップサック問題
シュークリーム専門店、pseudoカモノハシは創業3周年記念としてご当地グルメとのコラボレーションを計画している。グルメ系コンサルが提案したプランA〜Jの10件のご当地グルメとのコラボには、それぞれ費用と便益がある。この施策への予算が2000万円だとして、pseudoカモノハシは総便益が最大になるようにどのコラボ企画を採用するべきか。

定式化すると以下のようになります。
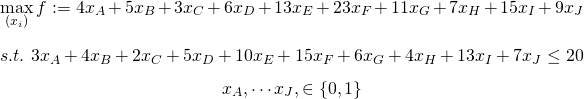
こちらにRのコードがあったので拝借しております。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
library(lpSolve) #便益 benefit <- c(4, 5, 3, 6, 13, 23, 11, 7, 15, 9) #費用 cost <- matrix(c(3, 4, 2, 5, 10, 15, 6, 4, 13, 7) , nrow=1) #予算 budget <- 20 ans <- lp(direction = "max", objective.in = benefit, const.mat = cost, const.dir = "<=", const.rhs = budget, all.bin = TRUE) |
これを実行すると、以下の結果が得られます。最大便益が31であること、それを実現するプランとしてE、G、Hが選ばれることがそれぞれ示しています。ただし、31を実現する解は他にもあります。
|
1 2 3 4 |
> print(ans) Success: the objective function is 31 > print(ans$solution) [1] 0 0 0 0 1 0 1 1 0 0 |
混合整数計画
シュークリーム専門店、pseudoカモノハシは傘下のパンケーキチェーン店、ヒッグス・シングスの3店舗から、「繁忙につき代替生産をお願いしたい」と言われた。ヒッグス・シングスのパンケーキは3店舗それぞれ味が異なり、それによってパンケーキの製造コストなども異なる。pseudoカモノハシの工房でパンケーキは生産可能ではあるが、そこそこに忙しいので生産できて15個が限度だと考えられる。そこで、以下の表が与えられたもとで、pseudoカモノハシはヒッグス・シングスの3店舗それぞれのパンケーキをどれだけ生産すれば利益が最大化されるか。
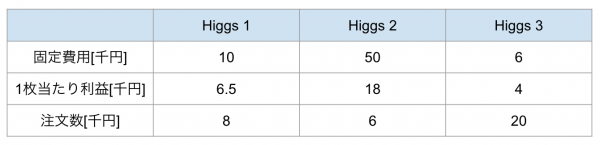
定式化すると以下のようになります。
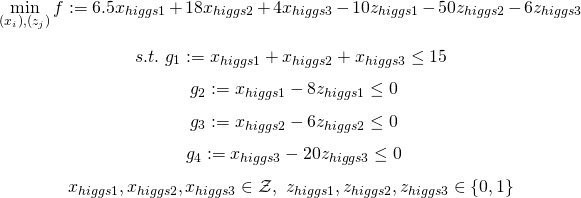
今回は調査の結果、Rglpkというパッケージがあることがわかったので、そちらを用います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
library(Rglpk) obj <- c(6.5, 18, 4, -10, -50, -6) mat <- matrix(c(1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, -8, 0, 0, 0, 0, -6, 0, 0, 0, 0, -20), nrow = 4) dir <- c("<=", "<=", "<=", "<=") rhs <- c(15, 0, 0, 0) types <- c("I", "I", "I", "B","B","B") max <- TRUE Rglpk_solve_LP(obj, mat, dir, rhs, types = types, max = max) |
このコードを実行すると、以下の結果が得られます。工房1と工房2で8個と6個の生産にコミットすることで、10万円の最大利益を実現できることが示されています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
> Rglpk_solve_LP(obj, mat, dir, rhs, types = types, max = max) $optimum [1] 100 $solution [1] 8 6 0 1 1 0 $status [1] 0 $solution_dual [1] NA $auxiliary $auxiliary$primal [1] 14 0 0 0 $auxiliary$dual [1] NA |
ウェーバー問題(非線形計画)
ウェーバー問題というのは、ORWikiによると以下の定義とされています。
施設・顧客間の距離に需要量を乗じたものの総和を最小化するような単一の施設の配置を、 平面上の任意の地点の中から決定する問題。
具体例で取り組んでみましょう。
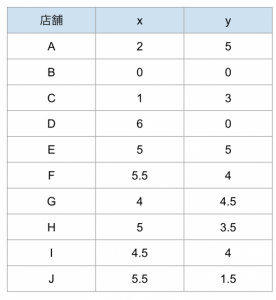
シュークリーム専門店、pseudoカモノハシは新しく食料庫を設置したいと考えている。店舗の位置が(x,y)座標で与えられているものとし、各店舗からの距離が最も小さくなるような位置に食料庫を設けるとしたらどこになるか、という問題。
定式化すると、以下のようになります。
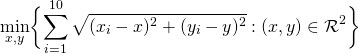
orlocaというパッケージを使えばウェーバー問題のような非線形計画問題を簡単に解くことができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
library(orloca) # A new unweighted loca.p object loca <- loca.p(x = c(2, 0, 1, 6, 5, 5.5, 4, 5, 4.5, 5.5), y = c(5, 0, 3, 0, 5, 4, 4.5, 3.5, 4, 1.5)) # Compute the minimum sol <- distsummin(loca) # Show the result sol # Evaluation of the objective function at solution point distsum(loca, sol[1], sol[2]) |
このコードを実行すると以下の結果が得られます。x座標が4.468528、y座標が3.843755の時に、距離の最小値が22.80259となることが示されています。
|
1 2 3 4 5 6 |
> # Show the result > sol [1] 4.468528 3.843755 > # Evaluation of the objective function at solution point > distsum(loca, sol[1], sol[2]) [1] 22.80259 |
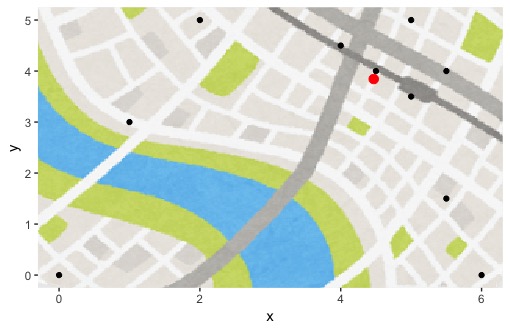
せっかくなので、いらすとやの画像を背景に結果などをプロットしてみます。赤い点が解となった点です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
#図にプロット library(ggplot2) library(png) image <- readPNG("map_open.png") dataset <- data.frame(x=loca@x, y=loca@y) g <- ggplot(data = dataset, aes(x = x, y = y)) g <- g + annotation_raster(image, xmin = -2, xmax = 8, ymin = -2, ymax = 8) g <- g + geom_point() g <- g + geom_point(data = data.frame(x=sol[1],y=sol[2]), aes(x = x,y = y), colour = "red", size = 3) g |
待ち行列
シュークリーム専門店、pseudoカモノハシ本店における来店客の行列に関してシミュレーションするものとする。
- pseudoカモノハシ本店は平均して1時間に50人来店し、それはポワソン分布に従うとされている。
- pseudoカモノハシ本店の商品は商品ごとに提供するまでにかかる時間が異なり、客はどれか1品を選択するが、その選択確率がおおむね決まっている。(以下の表)

進め方としては、まず、一様乱数を生成させ、ポアソン分布の分布関数の逆関数を求め、その逆関数に乱数を入力することで顧客の来店時間の間隔を生成します。
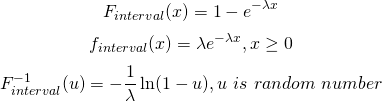
次に、顧客の選択する商品をシミュレーションするために別で一様乱数を生成し、その乱数の取る値に応じて商品を割り当てます。
そして、商品の提供に時間がかかることから、開始時間に商品の提供時間を足して、終了時間を求めます。ただし、来店時間に前の顧客がまだ商品を受け取れていないと、待ち時間が発生するので、来店時間の時点で終了していない場合はその分だけ開始時間が遅れます。
以下のRコードを作成してみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
library(tidyverse) #乱数の生成 set.seed(101) rand_uni <- runif(500) itm <- -1/(50/60)*log(1-rand_uni) ggplot(data = data.frame(x=itm), aes(x = x)) + geom_histogram(bins = 10) set.seed(5) rand_uni_demand <- runif(500) simulation <- data.frame(interval = itm, x=rand_uni_demand) %>% mutate(menu=if_else(x <= 0.25, "シュークリーム", if_else(x <= 0.5,"パンケーキ", if_else(x <= 0.8,"パフェ","ずんだ餅"))), time_required=if_else(x <= 0.25, 1.2, if_else(x <= 0.5,1.5, if_else(x <= 0.8,2.1,0.7)))) simulation <- simulation %>% mutate(arrival = cumsum(interval), start = NA) for (i in 1:nrow(simulation)) { if (i == 1) { simulation$start[i] <- simulation$arrival[i] } else { end_time <- simulation$time_required[i-1] + simulation$start[i-1] simulation$start[i] <- if_else( end_time > simulation$arrival[i], end_time, simulation$arrival[i]) } } #終了時間 simulation <- simulation %>% mutate(end = time_required + start) #待ち時間 simulation <- simulation %>% mutate(latency = start - arrival) #開始待ち人数 simulation <- simulation %>% mutate(numberof_wait= NA) for (i in 1:nrow(simulation)) { simulation$numberof_wait[i] <- sum(simulation$arrival < simulation$start[i]) } #空き時間 simulation <- simulation %>% mutate(idle_time = start - lag(end)) |
まず、来店間隔のシミュレーションですが、以下のようになります。
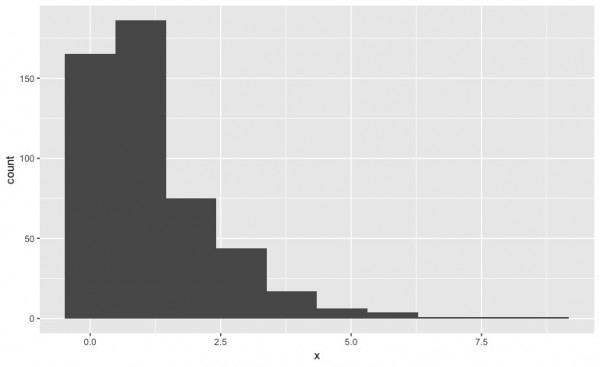
続いて、来店時間に応じた、待ち時間の推移です。
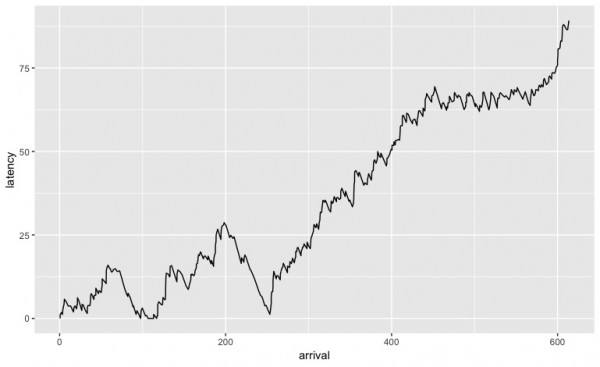
来店者の到来とともに、ぐんぐんと伸びているのがわかります。私はシュークリームに50分も待てないですね。
続いて、任意の顧客が開始した時に、すでに待っている客の数の推移です。
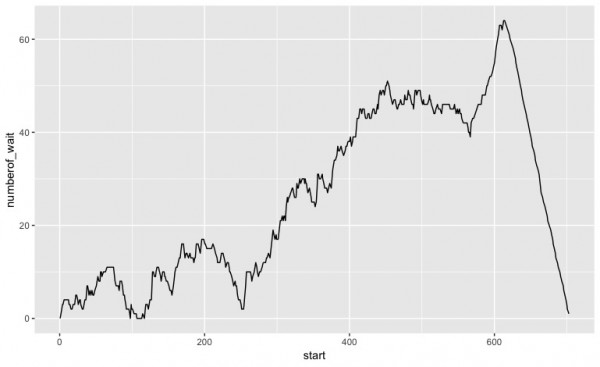
最後に、空き時間です。
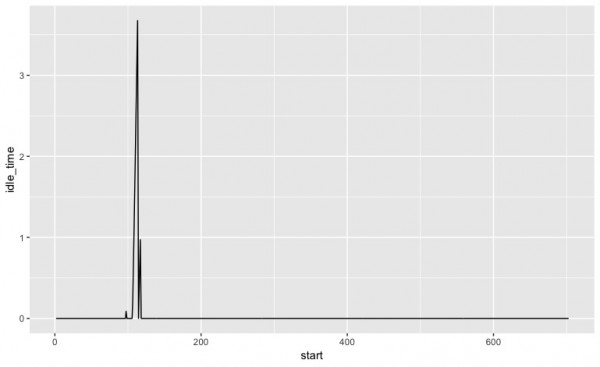
顧客が忍耐強く待つのであれば、ほとんどレジは休めていないという劣悪な労働環境になりそうですね。厨房の能力やレジの能力などを高める必要がありそうです。
最短路問題
シュークリーム専門店、pseudoカモノハシのオーナーSKUE氏は、いま店舗1にいるが、店舗6の店長との1on1があるため、向かおうと考えている。ついでに他の店舗の店長にも顔を出したいと考えており、他の店を経由して一番距離が短い経路を見つけたい。店舗と店舗の距離は以下のグラフのノード間のラベルで与えられているものとする。
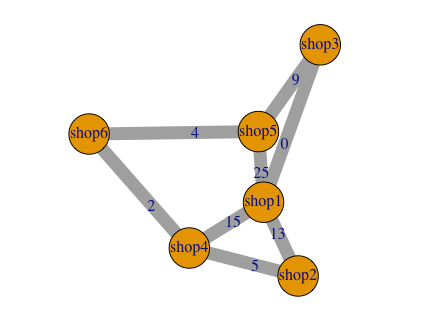
Rのigraphパッケージに「Shortest (directed or undirected) paths between vertices」というグラフ間の最短経路を見つける関数があるので、そちらを使います。この関数は最短経路問題を解く際に効率的とされる、ダイクストラ(Dijkstra)法というアルゴリズムを採用しています。具体的に使った例が載っているブログとしてこちらを参考にしています。
このグラフから、以下のようなデータを作っておきます。
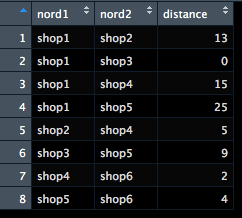
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
library(igraph) shortpath_dataset <- read_csv(file = "shortpath_problem.csv") net <- graph.data.frame(shortpath_dataset,directed=F) E(net)$weight <- shortpath_dataset$distance E(net)$label <- shortpath_dataset$distance E(net)$width <- 13 V(net)$size <- 35 plot(net) spv <- as.data.frame(shortest.paths(net)) #pに出発点、経由点、終着点を付値 p <- c("shop1","shop6") #aにダミーのデータを入れてリスト形式のオブジェクトを作成 a <- list("test") #ベクトル形式のオブジェクトbを作成 b <- 0 for(i in 1:(length(p)-1)){ #spに最短距離のノードリストを付値 sp <- get.shortest.paths(net, from=p[i], to=p[i+1]) #最短距離のノードリストをaに格納 a[[i]] <- V(net)$name[unlist(sp)] #距離行列の行と列を指定して距離を取り出すしてbに格納 b[i] <- spv[p[i], p[i+1]] } print(a) print(b) |
このコードを実行すると、以下のように、店舗1→店舗3→店舗5→店舗6の順番で店舗を巡ると最短経路である13が達成されることが示されます。
|
1 2 3 4 5 6 |
> print(a) [[1]] [1] "shop1" "shop3" "shop5" "shop6" > print(b) [1] 13 |
今回は店舗が少ないので、人間の目でも見つけることができますね。
巡回セールスマン問題
カワウソ急便の配達員が今、バレンタインデーの集配のためにpseudoカモノハシの店舗1(本店)にいる。配達員は他の全ての店舗の集配もする必要があり、集配後は確認のために本店に立ち寄る必要がある。どのようにして店舗を一度ずつ回れば移動距離が最も小さくなるかに関心がある。店舗ごとの位置は以下の図の通り。
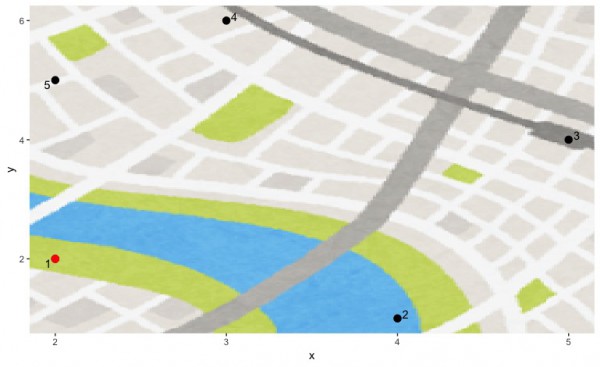
各地点の座標は以下の表で与えられている。
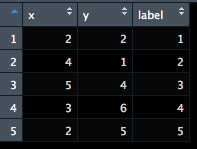
このような問題を巡回セールスマン問題と呼ぶが、 解く際は座標の点から各々店舗の距離を計算し、距離行列を作成し、その距離行列をもとに、1度しか通れないという制約条件を課しながら距離が最も小さくなる組み合わせを見つける。
RではTSP(Traveling Salesperson Problem)パッケージがあるので、proxyパッケージを使って距離行列を作ってしまえば、簡単に最適な順路を示してくれる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
#図にプロット library(ggplot2) library(png) library(ggrepel) image <- readPNG("map_open.png") dataset <- data.frame(x = c(2, 4, 5, 3, 2), y = c(2, 1, 4, 6, 5), label = c(1, 2, 3, 4, 5)) g <- ggplot(data = dataset, aes(x = x, y = y, label=label)) g <- g + annotation_raster(image, xmin = 0, xmax = 7, ymin = -1, ymax = 8) g <- g + geom_point(size = 3) g <- g + geom_point(data = data.frame(x=2,y=2,label=1), aes(x = x,y = y), colour = "red", size = 3) + geom_text_repel() g library(TSP) library(proxy) #距離行列の作成 data <- as.matrix(dist(dataset[1:2], method="Euclidean")) tsp <- TSP(data) tsp ## use some methods n_of_cities(tsp) labels(tsp) ## calculate a tour #start=1を指定することで1から始まるTSPを解いてくれる。methodでは様々な計算アルゴリズムが選択できる。 tour <- solve_TSP(tsp, method = "nn",start=1) tour[1:5] tour_length(tour) |
このコードを実行すると、以下のようになり、1→2→3→4→5→1と巡回することで総距離が12.641で済むことがわかる。
|
1 2 3 4 5 |
> tour[1:5] 1 2 3 4 5 1 2 3 4 5 > tour_length(tour) [1] 12.64099 |
これ以降は疲れ果てたので、実践というより紹介にとどまりますが、あしからず。
スケジューリングと集合被覆問題
Rでの事例が見つかりませんでした。Qiitaで以下のようなPythonによる実践があったので、それをもとにRで書き換えてみるのも良いと思います。(後日、追記したいと思います。)
組合せ最適化 – 典型問題 – 集合被覆問題
組合せ最適化 – 典型問題 – 勤務スケジューリング問題
NPV、IRR
ファイナンスで基本のNPV(Net Present Value)やIRR(Internal Rate of Return)の計算ですが、Package ‘FinCal’パッケージで簡単に計算できます。これくらい自分で書いてもいい気もしますが。このパッケージに割引率とキャッシュフローのベクトルを入力したらNPVを返してくれるnpv関数やirr関数があります。
|
1 2 3 4 |
> FinCal::npv(r=0.12, cf=c(-5, 1.6, 2.4, 2.8)) [1] 0.3348214 > FinCal::irr(cf=c(-5, 1.6, 2.4, 2.8)) [1] 0.1551911 |
データ包絡分析法
先日、ブレインパッドさんがこちらの記事で公開していたデータ包絡分析法(Data Envelopment Analysis:DEA)ですが、Rのコードが付いてなかったので漁ったところ、早稲田大学の逆瀬川先生がこちらでコードを公開しているようです。
DEAは同質な複数の事業体の相対的な効率性評価のための方法と定義されています。ブレインパッドさんの例ではコストを入力として、出力としての売上が効率的かどうかを見るために使われています。
パッケージに関しては、Data Envelopment Analysisでググったら、Benchmarkingというパッケージを見つけました。このパッケージは、少なくともブレインパッドさんのブログで紹介されている、DRS(Decreasing Returns to Scale)とFDH(Free Disposal Hull)は引数で選択可能のようです。
|
1 2 3 4 5 6 |
library(Benchmarking) x <- matrix(c(100,200,300,500,100,200,600),ncol=1) y <- matrix(c(75,100,300,400,25,50,400),ncol=1) dea.plot.frontier(x,y,RTS="fdh+",txt=TRUE) |
このコードを実行すると、ブログと似たような図が描けるようです。
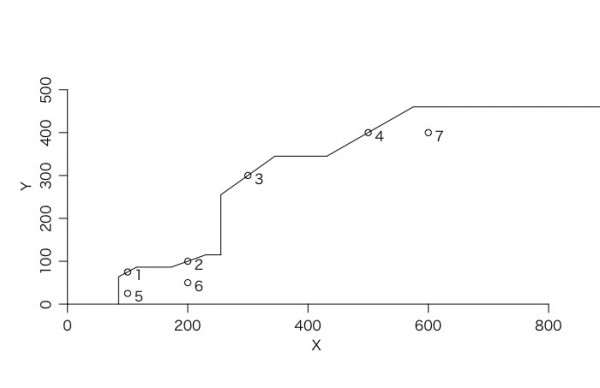
詳しくはドキュメントについている先行研究とかを見たいところです。
ポートフォリオ選択問題
これもファイナンスで基本となる、ポートフォリオ選択問題なのですが、投資家のリスク選好から無リスク資産(国債とか)とリスク資産(株式とか)をどれくらいの配分で持つのが効率的かを解くという問題になります。
どうやらtidyquantというパッケージを使うことで、効率的ポートフォリオを探索できるようです。こちらのドキュメント(Tidy_Portfoliomanagement_in_R)をまだ実践できていないですが、最終的に以下のような効率的ポートフォリオを描けるようです。
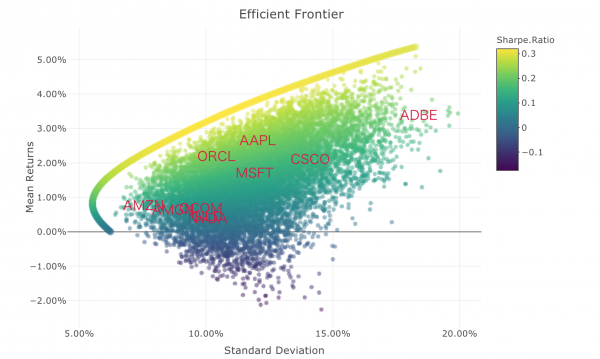
編集を終えて
まだまだ原理を深く理解できていないですが、いざ仕事の依頼が来た際の取っ掛かりとしては良いものが手に入った気がします。加えて、人間だと計算が厳しそうな問題を解けるというのは非常に面白いです。
「問題設定→定式化→コードに書き落とす」という一連の訓練を続けるとかなり力が付きそうな気がします。Rって統計学・機械学習以外にも本当に幅広く取り揃っていて飽きがこなくてよいですね。
参考情報
Excelで学ぶOR
サルでもわかる待ち行列
RでLinear Programming
問題解決の数理(’17)
Sensitivity Analysis 感度分析 もし○○○だったどうする?
Rでデータ解析を始めよう020 Rでナップサック問題を解いてみよう
CRAN Task View: Optimization and Mathematical Programming
Rで数理計画
RでOR:待ち行列モデル
[R]ggplot2によるグラフィックスで、図にPNG形式の画像を貼る
Rでクラスター分析〜距離行列の生成からクラスタリングまで
RでTSPの練習