最近はBayesian Statistics and Marketingという本に関心があって、そこで取り上げられているモデルをStanに落とし込めないか模索しています。
そこで順序プロビット（Ordered Probit）の推定が必要であることがわかったため、Stanでの適用事例を漁っていました。まだマーケティング事例への適用はうまくいってないですが、いったん順序プロビットを簡単にまとめて今後の備忘録としておきます。

順序プロビットとは

被説明変数yが連続潜在変数y∗に対応していると考えるとする。
潜在変数は観察できないが、被説明変数yは観察でき、これらの2つ変数の関係は次のように表される。
（今回扱うデータは3から8までの順序データのため、以下のような表記になる。）

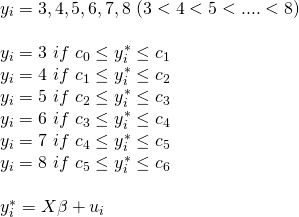
この対応関係は閾値メカニズムと呼ばれている。
各被説明変数をとる確率は以下のように記され、プロビットでは正規分布を扱うため以下のようになる。

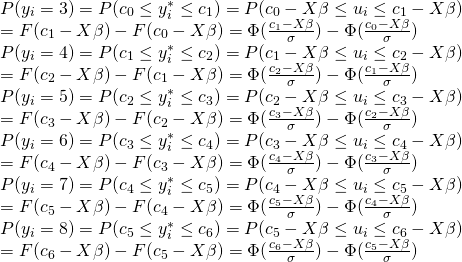
これらの選択確率からなる尤度関数を最大にしたものが順序プロビットの推定となる。（c0=−∞でc6=∞とする。σは1とする。）

このように、潜在的な順序関係を想定し、それを満たすように閾値とパラメータを推定する点において、潜在変数を用いたモデルの柔軟性の高さが感じられる。

なぜ順序プロビットを使うのか

マーケティング業務において扱うデータにおいて、NPSやアンケートなど順序尺度の質的変数が多いので、それらのデータを二値データに落とし込んだり、そのまま基数データとして扱うのではなく、適切に扱いたいというモチベーションがあります。加えて、順序尺度の質的変数をもとに予測する際は普通のOLSだと、今回のケースで3を下回ったり、8を超えたりする可能性があり、予測結果として使いにくいです。
アンケートの点数をそのまま被説明変数として回帰しているケースは、データアナリティクスにこだわりの無いメンバーとかであればままあることなので、順序プロビットの民主化というか、布教していきたいと思います。

今回扱うデータ

勝手ながら大人のirisだと思っているワインデータです。今回は赤ワインに絞って、品質に関する順序変数を被説明変数として、各変数との相関を見ていきます。
まずはGGallyパッケージのggpairs()関数を適用して傾向を掴みます。見にくいので是非コードを回して確かめてください。

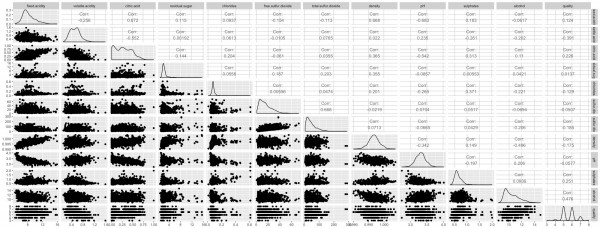
データに関する説明はワインの味（美味しさのグレード）は予測できるか？（１）で丁寧になされていますので、ご確認ください。

モデル

データセットに含まれる全部を含めて順序プロビットで回帰してみようと思います。
つまり、「酒石酸濃度、酢酸濃度、クエン酸濃度
残留糖分濃度、塩化ナトリウム濃度、遊離亜硫酸濃度
総亜硫酸濃度、密度、ｐＨ、硫酸カリウム濃度、アルコール度数」
の全てを使って赤ワインの質への影響を見ていきます。

Stanコード

最初に、Stanのユーザーガイド2.17の138ページにあるOrdered Probitのサンプルコードを使ってみたのですが、
収束しなかったので、初期値を設定するか弱情報事前分布を導入するかの判断が必要となります。
そこで、jabranhamさんが係数が平均0で分散10の正規分布に従うとするサンプルコードを書かれていたので、そちらを使って推定します。
書き換えているところはデータの制約くらいです。

data{
  int<lower=1> N; // number of obs
  int<lower=3> J; // number of categories
  int<lower=2> K; // num of predictors
  int<lower=0,upper=10> y[N]; // outcome var 
  matrix[N, K] x; // predictor vars 
}

parameters{
  ordered[J-1] tau; // thresholds
  vector[K] beta; // beta coefficients 
}

model{
  vector[J] theta;
  vector[N] xB;
  beta ~ normal(0, 10);
  xB <- x*beta;
  for(n in 1:N){
    theta[1] <- 1 - Phi(xB[n]-tau[1]);
    for(j in 2:J-1)
      theta[j] <- Phi(xB[n]-tau[j-1]) - Phi(xB[n]-tau[j]);
    theta[J] <- Phi(xB[n] - tau[J-1]);
    y[n] ~ categorical(theta);
  }
}

data{

int<lower=1> N; // number of obs

int<lower=3> J; // number of categories

int<lower=2> K; // num of predictors

int<lower=0,upper=10> y[N]; // outcome var

matrix[N, K] x; // predictor vars

}

parameters{

ordered[J-1] tau; // thresholds

vector[K] beta; // beta coefficients

}

model{

vector[J] theta;

vector[N] xB;

beta ~ normal(0, 10);

xB <- x*beta;

for(n in 1:N){

theta[1] <- 1 - Phi(xB[n]-tau[1]);

for(j in 2:J-1)

theta[j] <- Phi(xB[n]-tau[j-1]) - Phi(xB[n]-tau[j]);

theta[J] <- Phi(xB[n] - tau[J-1]);

y[n] ~ categorical(theta);

}

StanをキックするためのRコード

推定結果の可視化を行うためのcommon.Rは松浦さんのGitHubにあるものになります。

library(tidyverse)
library(rstan)
library(GGally)
library(shinystan)

rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())

wine_dataset <- read.csv("http://ieor.berkeley.edu/~ieor265/homeworks/winequality-red.csv", sep=";" )

y <- wine_dataset$quality - 2
x <- as.matrix(wine_dataset %>% select(-quality))
x <- scale(x)

# Visualization -----------------------------------------------------------
ggpairs(wine_dataset)


# Estimation --------------------------------------------------------------
stanmodel <- stan_model(file = "orderedprobit.stan")


N <- nrow(x)
J <- 6L
K <- ncol(x)

data_customer_list_test <- list(N=N,
                                J=J,
                                K=K,
                                y=y,
                                x=x)

fit <- stan(file = "orderedprobit.stan",
            data = data_customer_list_test,
            iter = 1000,
            chains = 4)

summary(fit)
traceplot(fit)

# Convergence Check -------------------------------------------------------
launch_shinystan(fit)

# Result Plot -------------------------------------------------------------
source('common.R')

ms <- rstan::extract(fit)
N_mcmc <- length(ms$lp__)


param_names <- c('mcmc', colnames(wine_dataset %>% select(-quality)))

d_est <- data.frame(1:N_mcmc, ms$b)
colnames(d_est) <- param_names
d_qua <- data.frame.quantile.mcmc(x=param_names[-1], y_mcmc=d_est[,-1])
d_melt <- reshape2::melt(d_est, id=c('mcmc'), variable.name='X')
d_melt$X <- factor(d_melt$X, levels=rev(levels(d_melt$X)))

p <- ggplot()
p <- p + theme_bw(base_size=18)
p <- p + coord_flip()
p <- p + geom_violin(data=d_melt, aes(x=X, y=value), fill='white', color='grey80', size=2, alpha=0.3, scale='width')
p <- p + geom_pointrange(data=d_qua, aes(x=X, y=p50, ymin=p2.5, ymax=p97.5), size=1)
p <- p + labs(x='parameter', y='value')
p <- p + scale_y_continuous(breaks=seq(from=-2, to=6, by=2))
p

library(tidyverse)

library(rstan)

library(GGally)

library(shinystan)

rstan_options(auto_write = TRUE)

options(mc.cores = parallel::detectCores())

wine_dataset <- read.csv("http://ieor.berkeley.edu/~ieor265/homeworks/winequality-red.csv", sep=";" )

y <- wine_dataset$quality - 2

x <- as.matrix(wine_dataset %>% select(-quality))

x <- scale(x)

# Visualization -----------------------------------------------------------

ggpairs(wine_dataset)

# Estimation --------------------------------------------------------------

stanmodel <- stan_model(file = "orderedprobit.stan")

N <- nrow(x)

J <- 6L

K <- ncol(x)

data_customer_list_test <- list(N=N,

J=J,

K=K,

y=y,

x=x)

fit <- stan(file = "orderedprobit.stan",

data = data_customer_list_test,

iter = 1000,

chains = 4)

summary(fit)

traceplot(fit)

# Convergence Check -------------------------------------------------------

launch_shinystan(fit)

# Result Plot -------------------------------------------------------------

source('common.R')

ms <- rstan::extract(fit)

N_mcmc <- length(ms$lp__)

param_names <- c('mcmc', colnames(wine_dataset %>% select(-quality)))

d_est <- data.frame(1:N_mcmc, ms$b)

colnames(d_est) <- param_names

d_qua <- data.frame.quantile.mcmc(x=param_names[-1], y_mcmc=d_est[,-1])

d_melt <- reshape2::melt(d_est, id=c('mcmc'), variable.name='X')

d_melt$X <- factor(d_melt$X, levels=rev(levels(d_melt$X)))

p <- ggplot()

p <- p + theme_bw(base_size=18)

p <- p + coord_flip()

p <- p + geom_violin(data=d_melt, aes(x=X, y=value), fill='white', color='grey80', size=2, alpha=0.3, scale='width')

p <- p + geom_pointrange(data=d_qua, aes(x=X, y=p50, ymin=p2.5, ymax=p97.5), size=1)

p <- p + labs(x='parameter', y='value')

p <- p + scale_y_continuous(breaks=seq(from=-2, to=6, by=2))

結果

まず、MCMCが収束したかどうかの判断ですが、ShinyStanに従うものとします。

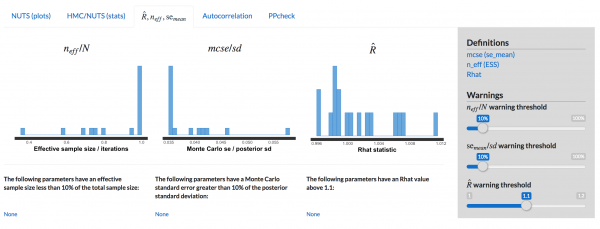
ShinyStanによる収束診断をクリアできています。

続いて、推定したパラメータです。

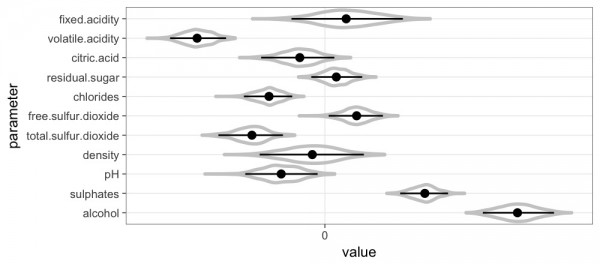
係数の符号がはっきりと分かれている、赤ワインの品質に影響を与えそうな変数としては、volatile acidity（酢酸濃度）、chlorides（塩化ナトリウム濃度）、total.sulfur.dioxide（総亜硫酸濃度）、sulphates（硫酸カリウム濃度）、alcohol（アルコール度数）のようです。

最後に、推定した閾値です。

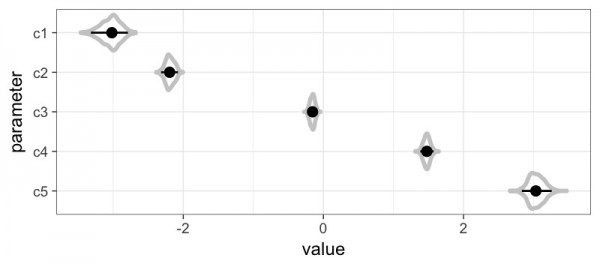
1と2の閾値が近く、2と3の開きが大きく、あとは比較的均等のようです。

比較

質的変数をそのまま重回帰した際の結果ですが、符号やその大小はあまり変わらないです。やはり予測の際にどの順序尺度の値に対応するかがわかるのが使う利点だと思います。

> dataset <- data.frame(cbind(y, x))
> multiple_regresion_model <- lm(formula = y ~ .,data = dataset)
> summary(multiple_regresion_model)

Call:
lm(formula = y ~ ., data = dataset)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.68911 -0.36652 -0.04699  0.45202  2.02498 

Coefficients:
                     Estimate Std. Error t value Pr(>|t|)    
(Intercept)           3.63602    0.01621 224.372  < 2e-16 ***
fixed.acidity         0.04351    0.04518   0.963   0.3357    
volatile.acidity     -0.19403    0.02168  -8.948  < 2e-16 ***
citric.acid          -0.03556    0.02867  -1.240   0.2150    
residual.sugar        0.02303    0.02115   1.089   0.2765    
chlorides            -0.08821    0.01973  -4.470 8.37e-06 ***
free.sulfur.dioxide   0.04562    0.02271   2.009   0.0447 *  
total.sulfur.dioxide -0.10739    0.02397  -4.480 8.00e-06 ***
density              -0.03375    0.04083  -0.827   0.4086    
pH                   -0.06386    0.02958  -2.159   0.0310 *  
sulphates             0.15533    0.01938   8.014 2.13e-15 ***
alcohol               0.29433    0.02822  10.429  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.648 on 1587 degrees of freedom
Multiple R-squared:  0.3606,    Adjusted R-squared:  0.3561 
F-statistic: 81.35 on 11 and 1587 DF,  p-value: < 2.2e-16

> dataset <- data.frame(cbind(y, x))

> multiple_regresion_model <- lm(formula = y ~ .,data = dataset)

> summary(multiple_regresion_model)

Call:

lm(formula = y ~ ., data = dataset)

Residuals:

Min 1Q Median 3Q Max

-2.68911 -0.36652 -0.04699 0.45202 2.02498

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 3.63602 0.01621 224.372 < 2e-16 ***

fixed.acidity 0.04351 0.04518 0.963 0.3357

volatile.acidity -0.19403 0.02168 -8.948 < 2e-16 ***

citric.acid -0.03556 0.02867 -1.240 0.2150

residual.sugar 0.02303 0.02115 1.089 0.2765

chlorides -0.08821 0.01973 -4.470 8.37e-06 ***

free.sulfur.dioxide 0.04562 0.02271 2.009 0.0447 *

total.sulfur.dioxide -0.10739 0.02397 -4.480 8.00e-06 ***

density -0.03375 0.04083 -0.827 0.4086

pH -0.06386 0.02958 -2.159 0.0310 *

sulphates 0.15533 0.01938 8.014 2.13e-15 ***

alcohol 0.29433 0.02822 10.429 < 2e-16 ***

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.648 on 1587 degrees of freedom

Multiple R-squared: 0.3606, Adjusted R-squared: 0.3561

F-statistic: 81.35 on 11 and 1587 DF, p-value: < 2.2e-16

考察

マーケティングにおいて、順序尺度の質的変数を扱う際に順序プロビットを積極的に使っていきたいと思いますが、アンケート分析を行う際は、ユーザーごとの評点の癖が点数に影響を与えている可能性があります。
そのため、点数の付き方がユーザーごとに違うとする階層モデルへの拡張を今後行っていくのが面白いと思いますし、実際に研究されている論文があります。

参考文献

StanとRでベイズ統計モデリング (Wonderful R)
stan-examples/limited-dv/oprobit.stan
stan-dev/stan users-guide-2.18.0.pdf
Stanによる順序ロジット回帰
 第9章順序選択モデル：年金投資選択問題
 Wine Quality Data Set
ワインの味（美味しさのグレード）は予測できるか？（１）
世界一簡単な収束[シナイ]Stanコード
 RStanとShinyStanによるベイズ統計モデリング入門

おまけ

数式をブログに載せる際は、こちら
Online LaTeX Equation Editor – create, integrate and download
でインタラクティブに数式を作成し、その結果を
QuickLaTex Publish Math on the Web without compromising quality
に貼り付けて画像を出力しています。

Stanで順序プロビット(Ordered Probit)の推定のためのメモ書き

順序プロビットとは

なぜ順序プロビットを使うのか

今回扱うデータ

モデル

Stanコード

StanをキックするためのRコード

結果

比較

考察

参考文献

おまけ

コメントを残すコメントをキャンセル

順序プロビットとは

なぜ順序プロビットを使うのか

今回扱うデータ

モデル

Stanコード

StanをキックするためのRコード

結果

比較

考察

参考文献

おまけ

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル