以前、テキストアナリティクスシンポジウムに参加した際に登壇者が機械学習のタスクにおいて分散表現を特徴量に使ったと言っていて、実務で使えるようにしたいと思ったので、調べた手法について記します。
先行研究
海外のブログ(Text Classification With Word2Vec)では、以下の手順で文書分類のための特徴量としてWord2Vecが用いられていました。
- STEP1:ロイターのコーパスをもとにWord2Vecを求める。(先行研究では100次元に圧縮しています。)
- STEP2:テキストごとに属する単語に対して、STEP1で求めた100次元の分散表現の平均値をとる。あるいは、TF-IDFのスコアで重み付けしたものを作る。これで100次元の分散表現が各テキストごとに用意できる。
- STEP3:STEP2で作った100次元の分散表現を用いて、テキストごとのラベルについてExtra Treesによる分類器を学習させる。
ざっとこんな感じのアプローチになっていました。”ベクトルの足し算が意味の足し算に対応する「加法構成性」”という考え方からのアプローチと言えるのでしょうか。
そのあと、ベースラインとの比較をしていましたが、結論としては、ラベル付きのトレーニングデータが非常に少ない場合において有利である傾向があったものの、SVMなどの既存手法より精度が出ているとは言えないような結果でした。
今回の事例におけるタスクではうまくいかなかったようですが、テキストアナリティクスシンポジウムにおいてはアツいとされていたので、自社のデータで適用するなどしておきたいです。
今回取り上げたブログやGithubにはPython2.X系のコードしかなかったため、3.X系で動くように一部変更するなどをしました。
以下で3系で動き、同様の結果が出ているものを載せています。
コード
コードの概要としては
・訓練データの作成
・モデルの定義
・モデルのベンチマーク
・結果の描写
です。
事前にテキストデータをダウンロードして手に入れておく必要がありますが、それに関してはターミナルで実行できるものなので、ここでは載せていません。参考文献のblog_stuff/classification_w2v/benchmarking.ipynbを参照ください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 |
#ライブラリの読み込み from tabulate import tabulate %matplotlib inline import matplotlib.pyplot as plt import seaborn as sns import pandas as pd import numpy as np from gensim.models.word2vec import Word2Vec from collections import Counter, defaultdict from sklearn.feature_extraction.text import CountVectorizer from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.ensemble import ExtraTreesClassifier from sklearn.naive_bayes import BernoulliNB, MultinomialNB from sklearn.pipeline import Pipeline from sklearn.svm import SVC from sklearn.metrics import accuracy_score from sklearn.cross_validation import cross_val_score from sklearn.cross_validation import StratifiedShuffleSplit TRAIN_SET_PATH = "r8-no-stop.txt" #行ごとにテキストをTabで分割し、ラベルデータとテキストデータに分ける。 X, y = [], [] with open(TRAIN_SET_PATH, "rb") as infile: for line in infile: label, text = line.decode('utf-8').split("\t") X.append(text.split()) y.append(label) X, y = np.array(X), np.array(y) print("total examples %s" % len(y)) #Word2Vecを実行する。 model = Word2Vec(X, size=100, window=5, min_count=5, workers=2) w2v = {w: vec for w, vec in zip(model.index2word, model.syn0)} #ベースラインとなる既存手法のモデルの準備 mult_nb = Pipeline([("count_vectorizer", CountVectorizer(analyzer=lambda x: x)), ("multinomial nb", MultinomialNB())]) bern_nb = Pipeline([("count_vectorizer", CountVectorizer(analyzer=lambda x: x)), ("bernoulli nb", BernoulliNB())]) mult_nb_tfidf = Pipeline([("tfidf_vectorizer", TfidfVectorizer(analyzer=lambda x: x)), ("multinomial nb", MultinomialNB())]) bern_nb_tfidf = Pipeline([("tfidf_vectorizer", TfidfVectorizer(analyzer=lambda x: x)), ("bernoulli nb", BernoulliNB())]) svc = Pipeline([("count_vectorizer", CountVectorizer(analyzer=lambda x: x)), ("linear svc", SVC(kernel="linear"))]) svc_tfidf = Pipeline([("tfidf_vectorizer", TfidfVectorizer(analyzer=lambda x: x)), ("linear svc", SVC(kernel="linear"))]) #単語の分散表現の平均値を求めるクラスの定義 class MeanEmbeddingVectorizer(object): def __init__(self, word2vec): self.word2vec = word2vec self.dim = word2vec.values() self.dim = next(iter(self.dim)) self.dim = self.dim.size def fit(self, X, y): return self def transform(self, X): return np.array([ np.mean([self.word2vec[w] for w in words if w in self.word2vec] or [np.zeros(self.dim)], axis=0) for words in X ]) #TF-IDFで重み付けした分散表現を求めるクラスの定義 class TfidfEmbeddingVectorizer(object): def __init__(self, word2vec): self.word2vec = word2vec self.word2weight = None self.dim = word2vec.values() self.dim = next(iter(self.dim)) self.dim = self.dim.size def fit(self, X, y): tfidf = TfidfVectorizer(analyzer=lambda x: x) tfidf.fit(X) max_idf = max(tfidf.idf_) self.word2weight = defaultdict( lambda: max_idf, [(w, tfidf.idf_[i]) for w, i in tfidf.vocabulary_.items()]) return self def transform(self, X): return np.array([ np.mean([self.word2vec[w] * self.word2weight[w] for w in words if w in self.word2vec] or [np.zeros(self.dim)], axis=0) for words in X ]) #Word2Vecを特徴量としてExtraTreesによる分類器を準備する。 etree_w2v = Pipeline([("word2vec vectorizer", MeanEmbeddingVectorizer(w2v)), ("extra trees", ExtraTreesClassifier(n_estimators=200))]) etree_w2v_tfidf = Pipeline([("word2vec vectorizer", TfidfEmbeddingVectorizer(w2v)), ("extra trees", ExtraTreesClassifier(n_estimators=200))]) #各モデルを実行し、クロスバリデーションスコアを計算し、出力させる。 all_models = [ ("mult_nb", mult_nb), ("mult_nb_tfidf", mult_nb_tfidf), ("bern_nb", bern_nb), ("bern_nb_tfidf", bern_nb_tfidf), ("svc", svc), ("svc_tfidf", svc_tfidf), ("w2v", etree_w2v), ("w2v_tfidf", etree_w2v_tfidf) ] scores = sorted([(name, cross_val_score(model, X, y, cv=5).mean()) for name, model in all_models], key = lambda x:x[0]) print(tabulate(scores, floatfmt=".4f", headers=("model", 'score'))) #棒グラフでクロスバリデーションスコアを比較する。 plt.figure(figsize=(15, 6)) sns.barplot(x=[name for name, _ in scores], y=[score for _, score in scores]) |
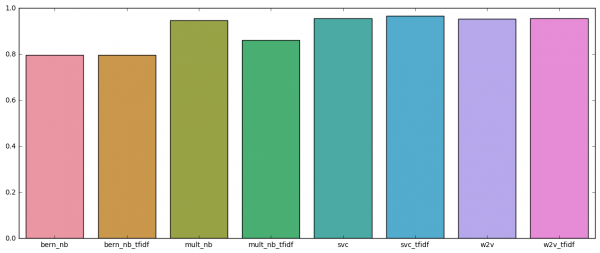
このようにSVCに負けている結果が出ます。
|
1 2 3 4 5 6 7 8 9 10 |
model score ------------- ------- bern_nb 0.7954 bern_nb_tfidf 0.7954 mult_nb 0.9467 mult_nb_tfidf 0.8615 svc 0.9562 svc_tfidf 0.9656 w2v 0.9526 w2v_tfidf 0.9549 |
比較の棒グラフはこんな感じ。
自社のテキストデータで是非とも試したい。
参考文献
岩波データサイエンス Vol.2
blog_stuff/classification_w2v/benchmarking.ipynb
分散表現(単語埋め込み)
Text Classification With Word2Vec