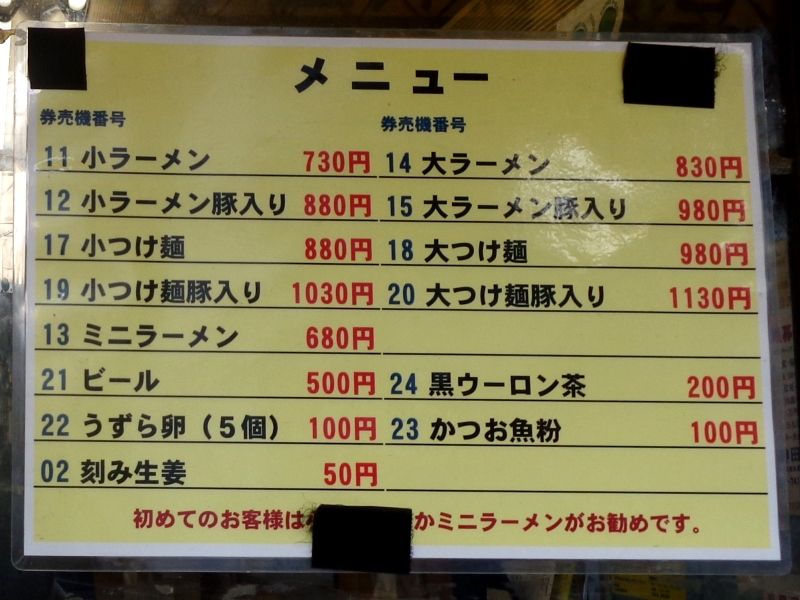
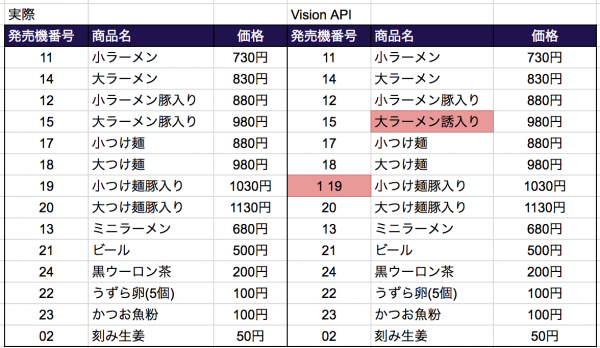
友人に『マーケティング・サイエンス入門』がおすすめと言われて読んだんですが、やっぱり実行できないとモヤモヤしてしまいますよね。そこで、登場する手法に関連したRのコードやらを集めてみました。
・BASSモデル
・多次元尺度法
・因子分析
・ロジット&プロビット
・分散分析
・クラスター分析
・判別分析
・決定木
・コンジョイント分析
・RFM分析
・共分散構造分析
BASSモデル
市場全体の規模が動的にどのように変化するかを予測するために使われるモデル。
R を使ってバスモデルを当てはめてみた – 廿TT
こちらにRのコードや適用例がいくつか載っています。
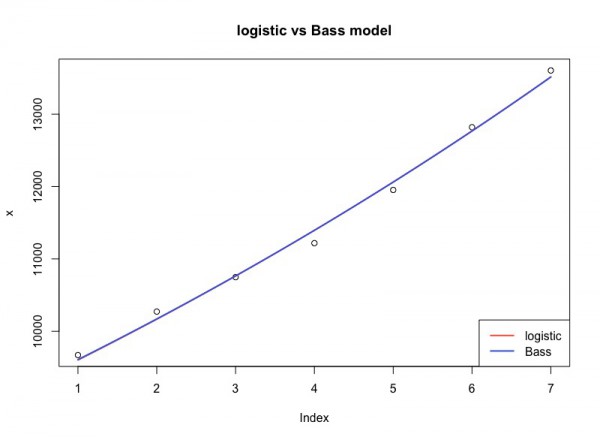
早速、私も携帯電話の加入契約数の時系列データを用いて、コードを実行してみました。データは平成25年版の総務省の情報通信白書の表から得ました。( 第2部 情報通信の現況・政策の動向 )
|
|
> fit_logis$value [1] 69833.02 > fit_bass$value [1] 68588.92 |
当てはまりはわずかながら、BASSモデルの方が良いようです。
多次元尺度法
多次元尺度法で遊んでみる(オレ流 R入門)
こちらのブログで山手線の駅間の距離データの可視化がなされています。
各駅ごとの距離からなる行列さえ用意すれば、cmdscale()関数を実行することで可能なようです。
今回はContaminatedMixtパッケージに含まれているワインのデータセットを使って多次元尺度法を適用してみようと思います。
データはこんな感じです。
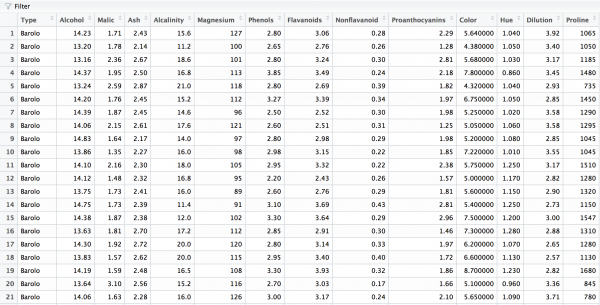
以下のコードで実行しました。
|
|
library(ContaminatedMixt) data(wine) wine.dist <- dist(wine[,-1]) wine.cmd <- cmdscale(wine.dist) plot(wine.cmd,type = "n") wine.lab <- factor(wine$Type) text(wine.cmd,labels = wine.lab,col = unclass(wine.lab)) |
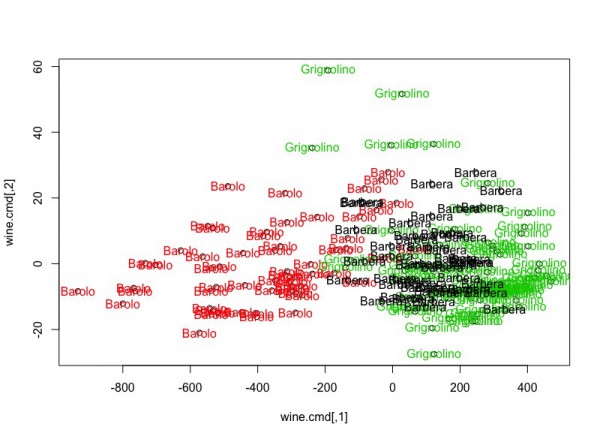
Barbera(バルベーラ)・・・基本的にはタンニンをあまり含まず、酸味の強い色の濃い赤ワインで庶民的。
Barolo(バローロ)・・・アルコール度数が高く、非常に重厚な味わいのワインでワインの王様と呼ばれる。
Grignolino(グリニョリーノ)・・・僅かにタンニンを感じるサッパリとした辛口の赤ワインで庶民的。
庶民と王様のワインは成分においても違いがありそうですね。
因子分析
psychパッケージというものがあるようです。こちらのサイトを参考にして進めます。( スナック菓子の食感についてRで因子分析してみた )
今回は大好きなwiskyのデータセットを使ってみます。( Classification of whiskies )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
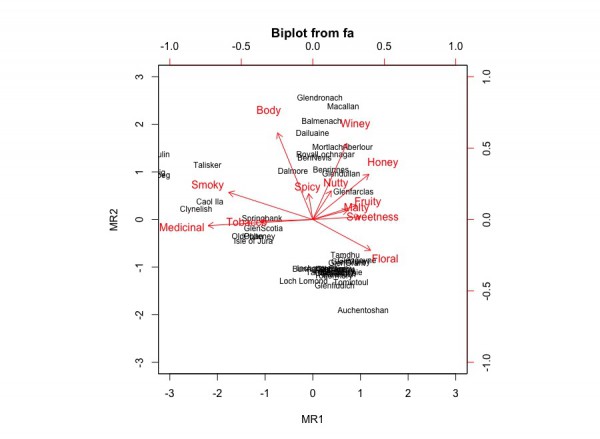
library(psych) library(GPArotation) whiskies <- read.csv("whiskies.txt", row.names = 1, stringsAsFactors = FALSE) rownames(whiskies) <- whiskies[,1] whiskies <- whiskies[,-1] whiskies <- whiskies[,-15] whiskies <- whiskies[,-14] whiskies <- whiskies[,-13] MAPminres <- vss(whiskies, fm="minres") print(MAPminres) MAPml <- vss(whiskies, fm="ml") print(MAPml) parallel <- fa.parallel(whiskies) print(parallel) res <- fa(whiskies, nfactors=2, fm="minres", rotate="oblimin") print(res, digits=3) biplot(res, labels=rownames(whiskies)) |
グレンフィディックやカリラやタリスカーがイメージ通りにプロットされています。ラガブーリンやアードベッグがはみ出しているのが残念ですが。
ロジット・プロビット
これらの手法はビルトインの関数でできてしまいますが、せっかくウイスキーのデータがあるので、薬っぽさに繋がりそうな変数を見つけてみます。
|
|
library(dplyr) whiskies2 <- whiskies %>% mutate(target=ifelse(whiskies$Medicinal>0,1,0)) whiskies2 <- whiskies2[,-which(colnames(whiskies2)=="Medicinal")] #ロジット model_logit <- glm(target ~ ., data=whiskies2, family=binomial(link="logit")) summary(model_logit) #プロビット model_probit <-glm(target ~ ., data=whiskies2, family=binomial(link="probit")) summary(model_probit) |
推定結果はこちらです。スモーキーさが関係しているのは納得です。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
> model_logit <- glm(target ~ ., data=whiskies2, family=binomial(link="logit")) > summary(model_logit) Call: glm(formula = target ~ ., family = binomial(link = "logit"), data = whiskies2) Deviance Residuals: Min 1Q Median 3Q Max -2.0173 -0.6313 -0.3509 0.2206 2.4214 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 4.39412 2.47716 1.774 0.0761 . Body -0.06226 0.51985 -0.120 0.9047 Sweetness -0.59932 0.46458 -1.290 0.1970 Smoky 1.35983 0.58327 2.331 0.0197 * Tobacco 1.75440 1.10595 1.586 0.1127 Honey -0.39101 0.46604 -0.839 0.4015 Spicy -0.22916 0.44331 -0.517 0.6052 Winey -0.86015 0.49829 -1.726 0.0843 . Nutty -0.56436 0.42843 -1.317 0.1878 Malty -1.17076 0.66243 -1.767 0.0772 . Fruity -0.33978 0.43754 -0.777 0.4374 Floral -0.64322 0.47291 -1.360 0.1738 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 107.023 on 85 degrees of freedom Residual deviance: 64.882 on 74 degrees of freedom AIC: 88.882 Number of Fisher Scoring iterations: 6 > model_probit <-glm(target ~ ., data=whiskies2, family=binomial(link="probit")) > summary(model_probit) Call: glm(formula = target ~ ., family = binomial(link = "probit"), data = whiskies2) Deviance Residuals: Min 1Q Median 3Q Max -1.9365 -0.6399 -0.3491 0.2064 2.4188 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 2.53606 1.41370 1.794 0.0728 . Body -0.05535 0.28834 -0.192 0.8478 Sweetness -0.36200 0.26740 -1.354 0.1758 Smoky 0.76890 0.32649 2.355 0.0185 * Tobacco 1.01419 0.64201 1.580 0.1142 Honey -0.19843 0.26056 -0.762 0.4463 Spicy -0.13537 0.25214 -0.537 0.5913 Winey -0.50543 0.27073 -1.867 0.0619 . Nutty -0.30335 0.24152 -1.256 0.2091 Malty -0.65838 0.36494 -1.804 0.0712 . Fruity -0.20000 0.25160 -0.795 0.4267 Floral -0.35983 0.26557 -1.355 0.1754 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 107.02 on 85 degrees of freedom Residual deviance: 65.06 on 74 degrees of freedom AIC: 89.06 Number of Fisher Scoring iterations: 7 |
ちなみに、多�項ロジットに関しては、mlogitパッケージを使えばできるようです。( 多項ロジット(Multinomial Logit), R – mlogit 使用メモ )大学院時代に多項ロジットはSTATAでよく使っていましたが、Rだとこのパッケージなんですかね。推定した係数の値の解釈が若干複雑だったりします。
分散分析
分散分析もビルトインの関数で実行することができます。今回はワインのデータを用いて、銘柄から30個ランダムサンプリングをした上で、アルコールに関して群間の母平均値が同じかどうかを確かめてみます。コードはこちらを参考にしました。( R による分散分析(一元配置) )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
A <- wine %>% filter(Type=="Barbera") sampleNum_A <- sample(nrow(A),30) A <- A[sampleNum_A,] B <- wine %>% filter(Type=="Barolo") sampleNum_B <- sample(nrow(B),30) B <- B[sampleNum_B,] C <- wine %>% filter(Type=="Grignolino") sampleNum_C <- sample(nrow(C),30) C <- C[sampleNum_C,] d <- data.frame(A = A$Alcohol, B = B$Alcohol, C = C$Alcohol ) library(reshape) x <- melt(d, variable_name = "group") res <- aov(value ~ factor(group), data = x) summary(res) |
推定結果はこちらです。アルコールに関しては、3群間において差があるようです。
|
|
> summary(res) Df Sum Sq Mean Sq F value Pr(>F) factor(group) 2 38.12 19.059 91.22 <2e-16 *** Residuals 87 18.18 0.209 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 |
クラスター分析
クラスター分析もビルトインの関数で実行可能です。ここでは参考文献( K-means Clustering 86 Single Malt Scotch Whiskies )のウイスキーのサンプルで取り上げられたK-mean法をそのまま紹介します。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
whiskies_k <- scale(whiskies) ssPlot <- function(data, maxCluster = 9) { # Initialize within sum of squares SSw <- (nrow(data) - 1) * sum(apply(data, 2, var)) SSw <- vector() for (i in 2:maxCluster) { SSw[i] <- sum(kmeans(data, centers = i)$withinss) } plot(1:maxCluster, SSw, type = "b", xlab = "Number of Clusters", ylab = "Within groups sum of squares") } ssPlot(whiskies_k) fit <- kmeans(whiskies_k, 4) whiskies <- data.frame(whiskies, fit$cluster) whiskies$fit.cluster <- as.factor(whiskies$fit.cluster) subset(whiskies, fit.cluster == 2) |
気になるクラスターの結果ですが、どうやらアイラ島系のウイスキーのクラスターを作れたようです。
|
|
> subset(whiskies, fit.cluster == 2) Body Sweetness Smoky Medicinal Tobacco Honey Spicy Winey Nutty Malty Fruity Ardbeg 4 1 4 4 0 0 2 0 1 2 1 Caol Ila 3 1 4 2 1 0 2 0 2 1 1 Clynelish 3 2 3 3 1 0 2 0 1 1 2 Lagavulin 4 1 4 4 1 0 1 2 1 1 1 Laphroig 4 2 4 4 1 0 0 1 1 1 0 Talisker 4 2 3 3 0 1 3 0 1 2 2 Floral fit.cluster Ardbeg 0 2 Caol Ila 1 2 Clynelish 0 2 Lagavulin 0 2 Laphroig 0 2 Talisker 0 2 |
判別分析
MASSパッケージで実行可能です。線形識別関数の実行例がこちらの参考文献に載っていたので、ワインのデータで試してみます。( 【Rによるデータサイエンス】線形判別分析 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
library(MASS) wine2 <- data.frame(wine[,-1],type=wine.lab) even.n <- 2*(1:(nrow(wine2)/2))-1 wine2.train <- wine2[even.n,] wine2.test <- wine2[-even.n,] #train Z.lda<-lda(type~.,data=wine2.train) Z.lda$means Z.lda$scaling Z.lda$means%*%Z.lda$scaling apply(Z.lda$means%*%Z.lda$scaling,2,mean) table(wine2.train[,ncol(wine2)],predict(Z.lda)$class) plot(Z.lda,dimen=1) plot(Z.lda,dimen=2) #test testResult <- predict(Z.lda,wine2.test[,-ncol(wine2)]) table(wine2.test[,ncol(wine2)],testResult$class) testResult$class plot(testResult$x,type="n") text(testResult$x,labels=wine2.test$type) |
判別関数得点
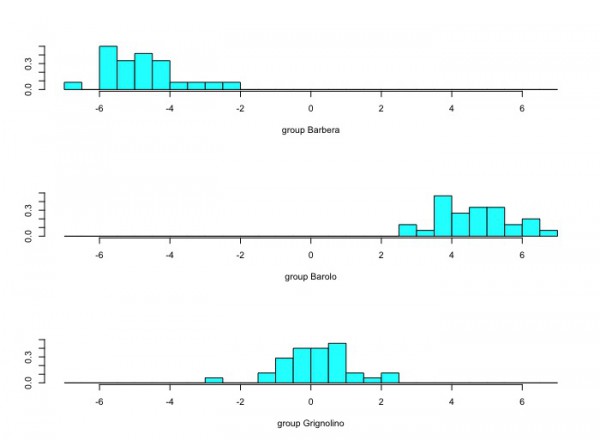
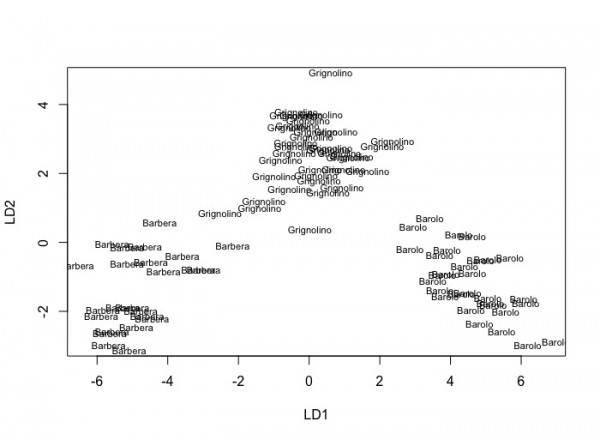
さすがパッケージ用のデータセットだけあって、綺麗に分類できたようです。誤分類は2件だけです。
|
|
> table(wine2.test[,ncol(wine2)],testResult$class) Barbera Barolo Grignolino Barbera 24 0 0 Barolo 0 29 0 Grignolino 0 2 34 |
決定木
決定木はrpartパッケージで実行します。ウイスキーのデータを使って、薬っぽさを決める条件を探してみます。コードはこちらを参考にしました。( R言語で決定木分析 )
|
|
library(rpart) library(partykit) library(epitools) result <- rpart(target~., data = whiskies2) plot(as.party(result)) |

コンジョイント分析
conjointパッケージなるものがあるようです。こちらの参考文献を元に紹介します。( Rでコンジョイント分析 )
まずは直交表を作ってみます。
|
|
library(conjoint) experiment <- expand.grid( 麺の量 =c("マシ","普通","少なめ"), ニンニク =c("マシ","普通","少なめ"), 野菜 =c("マシ","普通","少なめ"), あぶら =c("マシ","普通","少なめ") ) design.ort <- caFactorialDesign(data = experiment,type = "orthogonal") design.ort caEncodedDesign(design.ort) cor(caEncodedDesign(design.ort)) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
> design.ort 麺の量 ニンニク 野菜 あぶら 5 普通 普通 マシ マシ 10 マシ マシ 普通 マシ 27 少なめ 少なめ 少なめ マシ 34 マシ 少なめ マシ 普通 42 少なめ 普通 普通 普通 47 普通 マシ 少なめ 普通 57 少なめ マシ マシ 少なめ 71 普通 少なめ 普通 少なめ 76 マシ 普通 少なめ 少なめ > caEncodedDesign(design.ort) 麺の量 ニンニク 野菜 あぶら 5 2 2 1 1 10 1 1 2 1 27 3 3 3 1 34 1 3 1 2 42 3 2 2 2 47 2 1 3 2 57 3 1 1 3 71 2 3 2 3 76 1 2 3 3 > cor(caEncodedDesign(design.ort)) 麺の量 ニンニク 野菜 あぶら 麺の量 1 0 0 0 ニンニク 0 1 0 0 野菜 0 0 1 0 あぶら 0 0 0 1 |
残念ながら、面白そうなデータがないので、サンプルについているお茶のデータを使ってみます。
|
|
library(conjoint) data(tea) print(tprof) print(tlevn) print(tprefm) Conjoint(tprefm,tprof,tlevn) |
価格が効用に与える影響の可視化です。

RFM分析
ほくそ笑むの親分がeasyRFMパッケージを作っていたようです。( RFM 分析を簡単に実行できる R パッケージ easyRFM を作った )都合良く取引データがなかったので、kaggleの掲示板で落ちていたデータを使いました。( Sample of transaction data )
|
|
library(easyRFM) transaction <- read.csv("transactions-sample.csv") transaction <- transaction %>% mutate(payment=purchasequantity*purchaseamount) transaction <- transaction[,which(colnames(transaction) %in% c("id","payment","date"))] transaction$date <- as.character(transaction$date) result <- rfm_auto(transaction, breaks=3) head(result$rfm) result$classes |
結果は以下のとおりです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
> head(result$rfm) id Recency Frequency Monetary RecencyClass FrequencyClass MonetaryClass 1 86246 2013-04-23 12609 89333.08 1 3 3 2 86252 2013-03-26 12087 104436.35 1 3 3 3 12262064 2013-06-25 1101 5116.08 3 1 1 4 12277270 2013-06-19 1361 10820.49 3 2 2 5 12332190 2013-06-13 684 8709.90 2 1 1 > result$classes $recency_class [1] "2013-03-26 00:00:00 to 2013-05-11" "2013-05-11 00:00:01 to 2013-06-18" [3] "2013-06-18 00:00:01 to 2013-06-26" $recency_class_days [1] "92 to 46" "45 to 8" "7 to 0" $frequency_class [1] "681 to 1200" "1201 to 8600" "8601 to 13000" $monetary_class [1] "5100 to 9500" "9501 to 64000" "64001 to 110000" |
共分散構造分析
semパッケージで実行可能です。こちらの参考文献のデータを用います。( Rによるパス解析 )データはこちらにあります。( 練習用データ )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
library(sem) data01 <- read.csv(file="regpath.csv",header=T, fileEncoding="Shift-JIS") model01 <- specifyModel() 意欲 -> 学力, b1, NA 意欲 -> 適応, b2, NA 適応 -> 学力, b3, NA 学力 -> 自尊, b4, NA 学力 <-> 学力, v1, NA 自尊 <-> 自尊, v2, NA 適応 <-> 適応, v3, NA 意欲 <-> 意欲, v4, NA cov01 <- cov(data01[,2:5]) cov01 fit01 <- sem(model=model01, S=cov01, N=nrow(data01)) summary(fit01,rsquare=T,fit.indices=c("GFI","AGFI","SRMR","RMSEA","AIC","BIC")) stdCoef(fit01) |
Rを使った分析(SEM)
こちらの方がパスの図も出力できるので、良いかもしれません。
参考文献
マーケティング・サイエンス入門 — 市場対応の科学的マネジメント 新版 (有斐閣アルマ)